4.4 模拟水的方法

4.4.1 生成连续噪点－Perlin噪点

实时渲染所需的随机噪点生成有几种不同的方法。Ken Perlin，http://mrl.nyu.edu/~perlin/提出了一种产生连续噪点的方法可以比简单随机函数更类似与自然界的情况。图4－7显示了两者的区别：

基本Perlin噪点看起来不是很有趣，但如果把不同频率和振幅的噪点函数叠加在一起就能创建一个有趣地多的分形噪点，如图4－8所示：

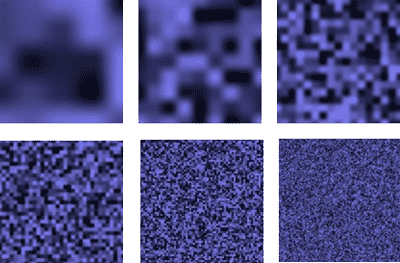
组合结果如图4－9所示：

每个层的频率是前者的两倍，这也是为什么层通常用8度表示（referred to as octaves）。要制作三维噪点动画使用二维噪点纹理也可以，更详细的解释可见[PN2，http://freespace.virgin.net/hugo.elias/models/m_perlin.htm]。

使用Perlin噪点作为水面的核心算法比以后要介绍的技术计算量小很多。Perlin噪点的主要问题是无法精确控制，只有频率和振幅可以很容易的改变，与外部物体的交互很难实现。

4.4.2 快速傅立叶变换

物理模拟很耗费资源。要更有效率，可以基于统计模型作为水面动画的核心算法。在这个模型中，波的高度是位置（位置是指不包含高度Z的水平XY坐标）和时间的变量。高度可以由一个函数决定，这个函数是一组有不同振幅和相位的正弦波，要快速获得振幅之和 ，可以使用反快速傅立叶变换。波的顶部很圆滑，还有其他方法可以增加波的陡度，使波看起来更波涛汹涌。

http://www.finelightvisualtechnology.com/docs/coursenotes2004.pdf

http://www.gamasutra.com/gdce/2001/jensen/jensen_01.htm

4.4.3 纳维－斯托克斯方程

在数学知识一章中提到的纳维－斯托克斯方程描述了不可压缩的流体的运动。作用力是重力、压力和粘滞力。这个方程很难解出，所以我们需要简化并离散方程以实现实时计算。一个有效的方法是使用高度图模拟相邻列的水体，用此方法，不需要明确指定海浪和其他表面失真，因为他们由物理状态自然生成。 [DSoSF，http://www.eecs.berkeley.edu/~job/Papers/obrien-1995-DSS.pdf] 介绍了一种技术，可以通过连接相邻栏的虚拟管道模拟水体变换，如图4－10所示：

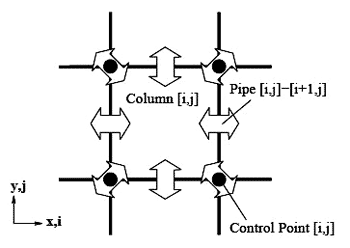
垂直栏通过一组有方向的水平管道与周围连接。这些管道让水的压力作用到整个水面。网格上的控制点可以通过采用分离相邻列。要和外部物体发生交互，表面可以作为一个单独的子系统将外部压力传递到整个水体网格（或子系统）上。如图4－11：

这些不同的子系统相互交互形成复杂的流体系统，如图4－12所示：

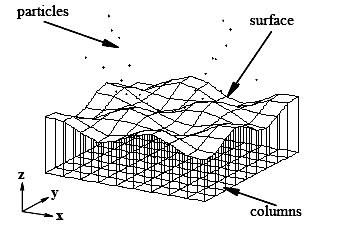
虽然它们很真实，但纳维－斯托克斯方程的每一步都很消耗资源，即使是对最新的显卡而言，也要限制网格的尺寸才能满足实时渲染的需要。如果不是实时渲染，例如电影泰坦尼克中使用的就是2048 x 2048 大小的网格，但这个大小在实时情况中是无法工作的。纳维－斯托克斯方程可用来模拟小的水面，如水池或喷泉。也存在其他渲染方法可以做同样的事，例如，一个简单的顶点偏移技术可以和纳维－斯托克斯方程组合起来实现与外部物体的更深入的互动。纳维－斯托克斯方程需要使用世界空间进行计算，而其他解决方案需要不同的网格空间，比如前面提到的投影网格技术。

纳维－斯托克斯方程解决二维网格要简单得多。通常情况下，二维网格就足够了，但二维网格有缺点，只有一个竖直力可以插入到系统中，所有外力的模拟必须要在竖直方向上近似，这会影响结果，比如风力通常是水平的，二维网格就会出现错误。

4.4.4 粒子系统

基于物理的方法最近非常受欢迎。硬件性能的提高使实时粒子系统成为可能。根据不同的情况，基于顶点和基于像素的解决方案都可以实现大量独立的粒子的运动。粒子系统技术可与其他水动画方法组合获得更为真实的结果。粒子系统需要解决的问题是：如何使粒子运动，以及粒子应作为怎样的物体。整个系统可以有速度向量，但速度向量无需通过整个水流。如图4－13所示：

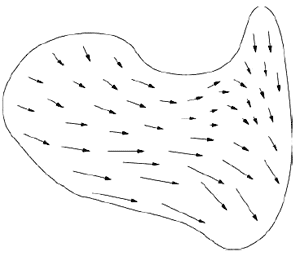
第二个问题是：我们的粒子也可以忽略大小和质量。但他们可以携带其他类型的信息使其他类型的相互作用成为可能，例如，颜色，温度和压力，这取决于想要达到的效果。

粒子遵循物理规律运动，他们的运动可以在前面讨论过的速度向量贴图的帮助下计算得到，要在图形硬件上计算，一个纹理必须储存粒子的位置，其位置采样到纹理。这些纹理被称为粒子纹理贴图，如图4－14：

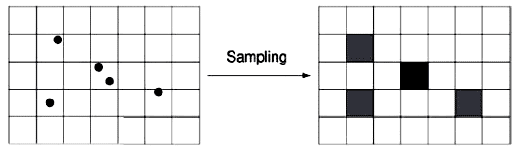
要在下一时间步长获取粒子位置，我们追踪这些粒子，就像他们独自沿速度矢量图移动那样。这种做法被称为forward-mapping。如图4－15所示：

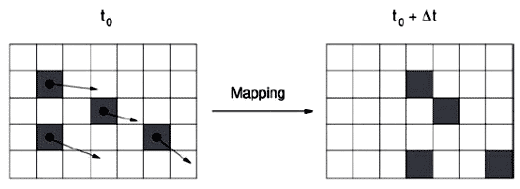
这个技术有一些问题。首先，如果流速过小，有些粒子会永远停留在相同的网格单元中，因为每次循环中它们被认为是从网格单元的中心出发的，如果不能在一个时间步长中离开网格单元 ，它们会重新回到中心。第二，基于前面的同样理由，有些网格单元总是空的，这会导致粒子静止不动。

为了克服这些问题，可以用backward mapping代替forward mapping。对于每一个网格单元，我们计算粒子来自于哪个单元。然后，我们使用原始单元的颜色确定当前单元的颜色。如果使用插值，周围的颜色也可以考虑，这样我们就能够避免静止的粒子，如图4－16所示：

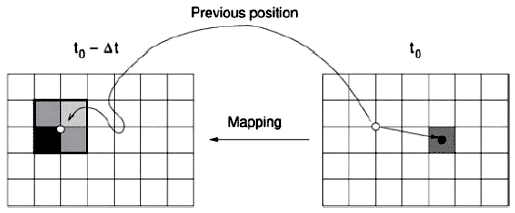
速度贴图和粒子贴图都存储在单独的纹理中，纹理有两个组成部分。一个标准的2D纹理通过这种方式表示，第三维是近似添加的以提升性能。Offset纹理是硬件支持的，所以沿速度场的移动可以通过硬件实现。Inflow 和outflow（粒子生成和清除）超出本文范围。更详尽的解释和源代码中可以在[ SHADERX ]中找到。

粒子系统是实现外部物体与水面的实时交互的很好的解决方案。它们也可以有效地表现水面动画，但通常它们与其他技术一起应用。流动的水，水滴，喷溅，瀑布都可以通过粒子系统实现。

喷溅在[DSoSF，http://www.eecs.berkeley.edu/~job/Papers/obrien-1995-DSS.pdf] - James F. O’Brien and Jessica K. Hodgins: Dynamic Simulation of Splashing Fluids一文中作为一个子系统，当表面的一个部分具有较高的上升速度时，粒子不会发生交互，它们只会在重力的作用下落回到水面，然后将这些粒子从系统中移除。

[DWAaR，http://www.gamasutra.com/view/feature/3036/deep_water_animation_and_rendering.php] - Deep-Water Animation and Rendering一文中使用了类似的粒子模型模拟喷溅。只考虑简单的牛顿动力学：喷溅位置的速度影响了初速度，它可以由重力、风力和其他可能的外力改变。渲染混合了alpha-transparency和additive-alpha精灵。欲了解更多细节和截图，请参阅Deep-Water Animation and Rendering。

发布时间：2009/4/22 下午4:14:59  阅读次数：9954