第七节、全反射

一、全反射现象

光从光密媒质射入光疏媒质时，折射角大于入射角。由此可以预料，当入射角增大到某一角度时，折射角将等于 90°，入射角再增大，就不再有折射光线了。

上述现象可以用图 5–23 所示的半圆形玻璃砖来观察。让光线沿着半圆形玻璃砖的半径射到直边上，可以看到，一部分光线从直边折射到空气中，一部分光线反射回玻璃。逐渐增大光线的入射角，将会看到，折射光线离法线越来越远，而且折射光线越来越弱，反射光线越来越强，当入射角增大到某一角度时，折射光线消失，只剩下反射光线，光全部反射回玻璃中，这种现象叫做全反射。

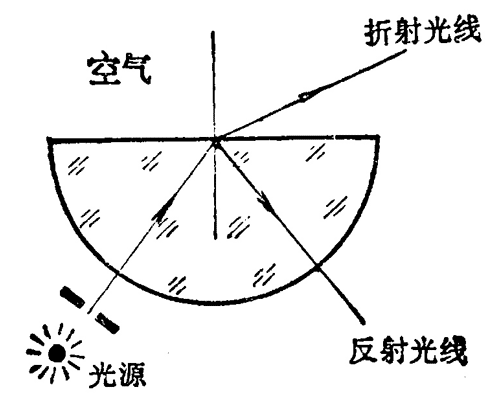
二、临界角

折射角等于 90° 时的入射角叫做临界角。光线从光密媒质射入光疏媒质，当入射角大于临界角时，就发生全反射现象。

利用光的折射定律，可以求出各种媒质对空气（或真空）的临界角。如果用 C 表示临界角，n 表示媒质的折射率，那么，由于空气对该媒质的折射率等于 ，所以

$$\frac{\sin C}{\sin {90}^{\circ }}=\frac{1}{n}$$

由此可得                                                         sin C = $\frac{1}{n}$

因此，已知媒质的折射率，利用上式就可以求出这种媒质对空气（或真空）的临界角。

光的全反射现象在自然界中经常可以看到。水或玻璃中的气泡看起来特别明亮，就是因为光从水或玻璃射向气泡时，在界面发生全反射。露水珠或喷泉的水珠，在阳光照耀下格外明亮，也是因为射进水珠的光在水珠内发生全反射。

三、光导纤维

光从玻璃射入空气时，如果入射角大于临界角，就发生全反射，使光不能从玻璃射到空气中。这一现象使人们受到启发，试图用玻璃棒来传输光。如图 5–24 所示，把一根弯曲的玻璃棒插在暗盒的一边，打开盒里的电灯，可以看到从玻璃棒的下端有明亮的光传出来，如果照在纸上，就出现一个明亮的光斑，这是因为从玻璃捧上端进入棒内的光线，在棒的内壁上发生全反射；经过多次全反射，光线最后从棒的下端传出来。

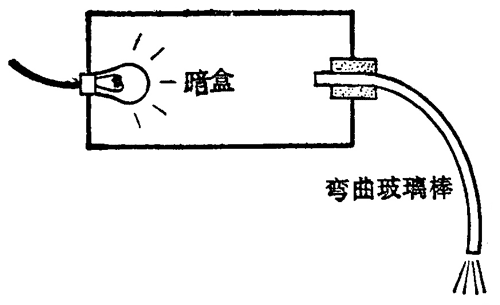
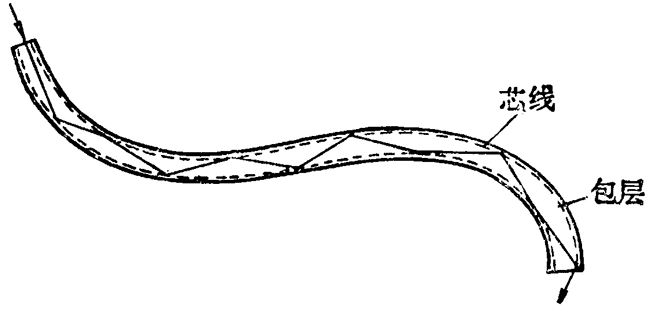
现代科学技术中用的光导纤维，就是利用上述现象制成的，光导纤维简称光纤，是一种比头发还细的玻璃丝，这种玻璃丝分为内外两层（芯线和包层），芯线的折射率比包层的折射率大，光从芯线射向包层时能发生全反射，这样光就在芯线内从光纤的一端传输到另一端（图 5–25）。

如果把许多光纤并成束，并使束中各条光纤的相对位置保持不变，就可以用来传递图像（图 5–26）。医学上用光纤来观察人体内脏的内窥镜，例如胃镜，就是用这个道理制作的。

光导纤维在现代科学技术中有重要的应用，就象无线电技术中把信号调制到无线电波上一样，把要传送的信号调制到光波上，让光载着信号沿光导纤维传送出去，就可以实现光纤通讯。光纤通讯能够同时传送大量信号，对信息的传输能力很大，这是它的突出优点。采用光纤通讯将会引起通讯技术的重大变革，光纤通讯在一些先进国家正在进入实用阶段。我国也在努力提高光纤技术的水平，积极进行光纤通讯试验，以适应现代科学技术革命的需要，这方面有许多工作等待人们去做。

阅读材料：海市蜃楼

夏天，在平静无风的海面上，向远方望去，有时能看到山峰、船舶、楼台、亭阁、集市、庙宇等出现在远方的空中，古人不明白产生这种景象的原因，对它作了不科学的解释，认为是海中蛟龙（即蜃）吐出的气结成的，因而叫做“海市蜃楼”。1981 年 8 月 19 日文汇报曾以《蓬莱阁上观胜景，庙岛海面出蜃楼》为题，登载了这年 7 月 10 日下午在山东省蓬莱市海面上出现海市蜃楼的消息，当时有四、五百游人观赏了这一奇异景象。

海市蜃楼是光在密度分布不均匀的空气中传播时发生全反射而产生的，夏天，海面上的下层空气，温度比上层低，密度比上层大，折射率也比上层大。我们可以把海面上的空气看作是由折射率不同的许多层气体组成的，远处的山峰、船舶、楼房、人等反射出来的光线射向空中时，由于不断被折射，越来越偏离法线方向，进入上层空气的入射角不断增大，以致发生全反射，光线反射回地面，人们逆着光线看去，就会看到远方的景物悬在空中（图 5–27）。

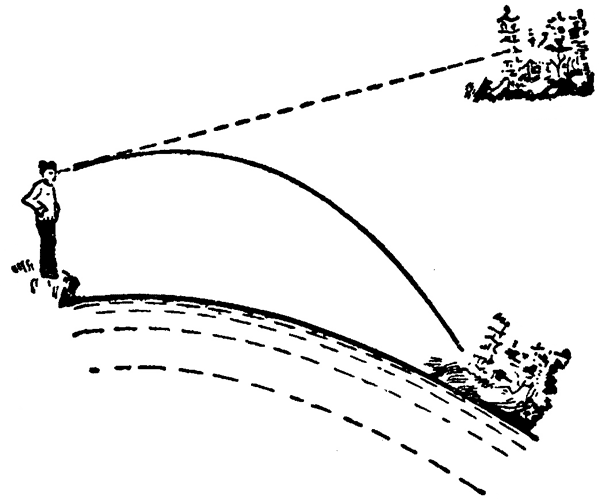
在沙漠里也会看到海市蜃楼现象，太阳照到沙地上，接近沙面的热空气层比上层空气的密度小，折射率也小。从远处物体射向地面的光线，进入折射率小的热空气层时被折射，入射角逐渐增大，也可能发生全反射，人们逆着反射光线看去，就会看到远处物体的倒影（图 5–28），仿佛是从水面反射出来的一样，沙漠里的行人常被这种景象所迷惑，以为前方有水源而奔向前去，但总是可望而不可及。

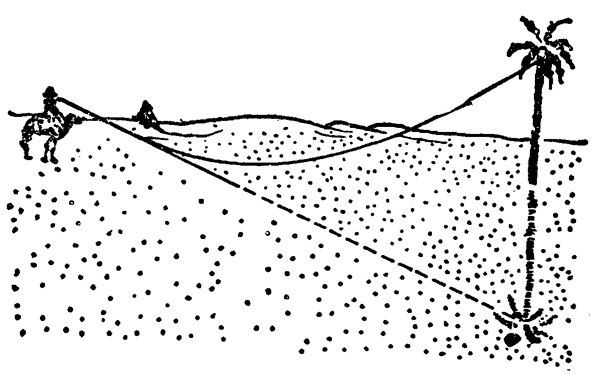
在炎热夏天的柏油马路上，有时也能看到上述现象。光线被贴近路面的热空气全反射，从远处看去，路面显得格外明亮光滑，就象用水淋过一样。

练习五

（1）水和金刚石的临界角各是多大？

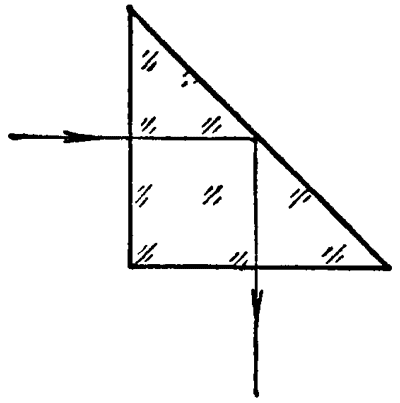
（2）图 5–29 表示一个横截面为等腰直角三角形的玻璃棱镜。当光从它的一个直角边垂直射入时，就从另一个直角边垂直射出来，而没有光从斜边射出，这种棱镜可以使光的传播方向改变 90°。说明它的道理。

（3）光线从空气射入水中时，光线在水中的折射角最大为多少度？

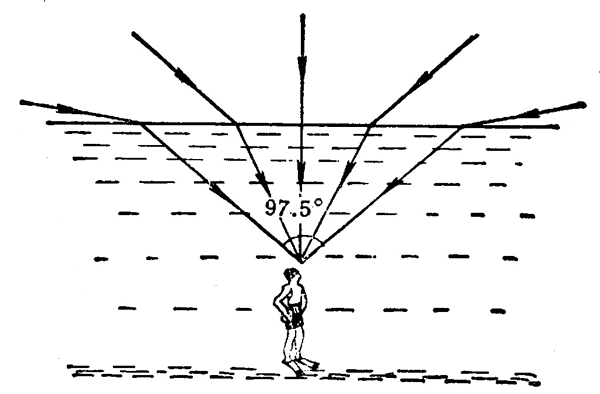
（4）潜水的人在水面下能看到水面上的全部景象，因为水面上 180° 范围内射入水中的光线全部集中在水下 97.5° 的视野内（图 5–30），试说明它的道理。

发布时间：2025/5/11 上午8:16:07  阅读次数：726