第五节、光的折射

光从空气斜射到玻璃上，在界面上一部分光线发生反射，回到空气中；另一部分光线射入玻璃中，并改变了原来的传播方向（图 5–19）。光从一种媒质射入另一种媒质时，传播方向发生改变的现象，叫做光的折射。

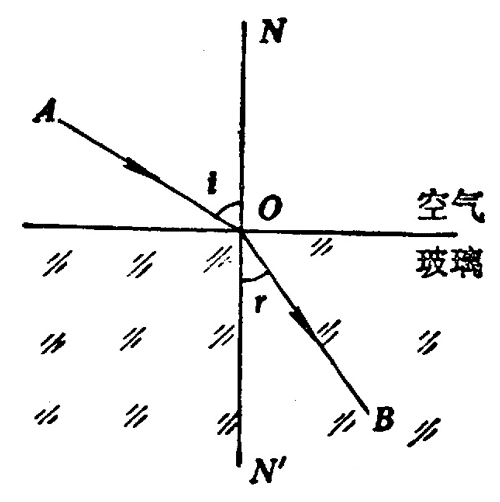
改变入射光线的方向，折射光线的方向也随着改变。折射光线与法线间的夹角叫做折射角。折射角与入射角之间有什么关系呢？这个问题，历史上经过一千多年才研究清楚，公元二世纪，希腊天文学家托勒密（100—170）测量了折射角与入射角，积累了大量的数据。根据测量结果，托勒密认为折射角与入射角成正比。这个结论在入射角较小时大体上是正确的，入射角较大时就不成立了。下表是实验测得的光从空气射入玻璃时一组入射角与折射角的数据。从表中可以看出，当入射角大于 20° 时，入射角 i 与折射角 r 的比值 \(\frac{i}{r}\) 随着入射角的增大有较大的变化，不是恒量。

为了研究折射角与入射角之间的数量关系，在很长的一段时间里，许多科学家作了多方面的尝试，直到 1621 年才由荷兰科学家斯涅耳（1580—1626）发现了这个关系：入射角的正弦跟折射角的正弦之比是个常数，即 \(\frac{{\sin i}}{{\sin r}}\) = 常数。

人们在研究折射现象时早已发现，折射光线位于入射光线和法线所在的平面上，折射光线和入射光线分居在法线的两侧，结合斯涅耳的发现，我们可以把光的折射定律表述如下：

（1）折射线在入射光线和法线所在的平面上，折射光线和入射光线分居在法线的两侧；

（2）入射角的正弦跟折射角的正弦之比为一常数，即

\[\frac{{\sin i}}{{\sin r}} = 常数\]

在折射现象中，光路也是可逆的。在图 5–19 中，如果光线沿 BO 从玻璃射入空气中，即入射角为 r，空气中的折射光线将沿 OA 前进，即折射角为 i。这样，光线由其他媒质射入空气中时，折射角大于入射角。

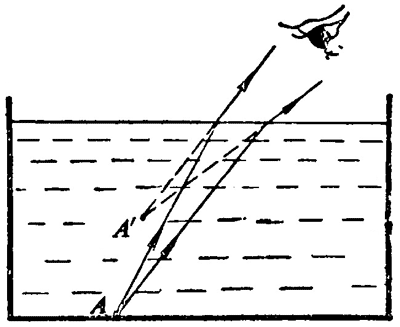
利用光的折射，可以解释水的视深比实深浅的现象。图 5–20 表示一个装有水的容器，A 是容器底上的一点，从 A 点发出的光线由水中射入空气时，折射角比入射角大，折射光线远离法线。折射光线进入眼中后，我们根据光沿直线传播的经验，就觉得它们是从 Aʹ 点发出的。Aʹ 在 A 的上方，所以看到容器的底部上升，水变浅了。

发布时间：2025/5/7 下午8:12:14  阅读次数：231