4.3 性能优化

因为是硬件处理三角形，所以无法回避表面镶嵌。真正的水面是持续不断的，但电脑绘图使用的是多边形，所以需要使表面离散。更多三角形可以描述更详细的虚拟世界，但也需要更多顶点。每个图形程序员都要在复杂性和性能之间找到平衡，即在真实度和速度之间找到平衡。

4.3.1 经典LOD算法

根据Level Of Detail（ LOD值）的概念，一个复杂的对象可以简化为不同程度的细节。屏幕上的物体越小，细节越少以获得更好的性能。图4－2展示了LOD：

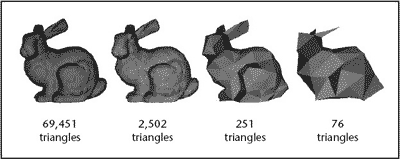
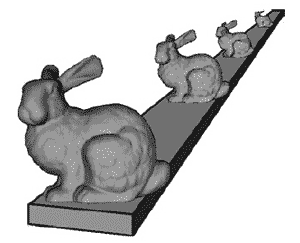
如果兔子很小或距离较远，我们无法分辨高精度模型和低精度模型之间的区别，如果视觉上没有差别，要提高性能，我们可以只绘制较少三角形的兔子模型，如图4－3：

还有一种LOD是连续LOD。这种LOD不是在运行前创建不同细节的模型，而是实时将模型简化到想要的细节。我们只需存储最高细节的兔子，应用程序会删除不必要的多边形以提升性能。这样一来， LOD值粒度好得多，还可以使用前面生成的模型层次，但应用程序变得更加复杂。细节可参考[LODf3DG] - Morgan Kaufmann: Level of Detail for 3D Graphics 。

4.3.2水面的LOD算法

LOD技术也可用于水面渲染。如果水面是由大量三角形构成的，例如，一个三角形带，这一三角形带可以比使用同等大小的三角形获得更加真实的优化结果。使用这一方法最主要的问题是应该如何排列三角形。

下面的方法是在[BMELAB2] - Game development laboratory material 2, BME, AUT中提出的。使用30 × 30大小的网格（三角带）模拟水面的可见部分，这意味着总是在相机前方进行转换。可以在其他坐标(z = f(x,y))的连续函数的帮助下计算高度，这样顶点位置的放置可以没有任何限制。如果我们使用同等大小的三角形带，距离远的三角形会变得很小。

可以通过顶点置换优化性能。遥远的三角形太小，他们应转换为对相机来说大致相同的面积。还必须考虑近裁和远裁平面及三角形带的宽度使在相机中看见到整个水面。还有一个问题是将三角带的高度变成相同高度。下面的双曲函数给出了取决于行数的水平位置：

\[f(k) = \frac{1}{{1 - \frac{k}{{{k_{\max }}}}}}\]

公式中的k是第几行，kmax是总行数。三角形的第一行（k＝0）水平距离是0，最后一行(k＝ k_max －1) 收敛至无穷大。

因为我们不会在无穷远处绘制物体，上面的方程需要进行缩放。在渲染前我们应该已经有了近裁和远裁平面，这意味着，只有在这两个平面之间的三角形才会被渲染。如果D_max是远裁平面距离，D_min是近裁平面距离，下列方程可以置换和缩放点的坐标：

\[f(k) = \frac{{{D_{\max }}}}{{{k_{\max }} - 1}}(\frac{1}{{1 - \frac{k}{{{k_{\max }}}}}} - 1 - {D_{\min }})\]

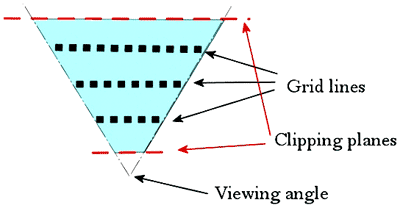
例如，如果在0至1000范围之内的物体要渲染，水面可以缩放到同样大小，只需把Dmax设置成1000，Dmin设置成0。网格行必须比从相机可见的相同大小宽得多。如图4－4所示：

在[BMELAB2] - Game development laboratory material 2, BME, AUT一文中，使用如下公式让三角边可以缩放以匹配视角的两边：

\[f(i) = \frac{{i - \frac{{{i_{\max }} - 1}}{2}}}{{{i_{\max }}}} \cdot d \cdot r\]

公式中的i是实际列序号，i_max是列总数，d是行间距（之前以计算），r是视角比例（例如4：3或16：9）有用链接： Terrain LOD: Runtime Regular-Grid Algorithms

4.3.3 使用投影网格（Projected grid）

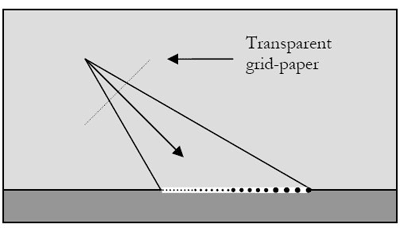
LOD算法判断哪些顶点使用得更频繁，哪些应忽略，实现了很漂亮的实时水面渲染。但如果相机移动，那么屏幕上的顶点位置也会发生变化。Projected grid算法通过以下几步让顶点在相机空间中更加平滑： 在相机空间创建一个规则网格与相机正交。 将这个网格投影到对应平面。 将网格转换到世界空间。 设置偏移，波浪等。 渲染网格例如，如果你将一张带网点的纸放在投影灯的前面，网格会投影到桌面上，如图4－5所示：

这些网格是规则和光滑的，这也是我们处理水面顶点想要达到的目标。

在[ IAoOW ] （译者：不知是哪篇文章）一文中还提到了自适应水面网格的使用。包含水面网格切换的相机移动让每个顶点都有近似相同的投影。但也带来了新的问题，因为不正确的表面近似，表面的法线无法利用有限差分技术估计。要确定法线需要 使用分析方法。如图4－6所示 ：

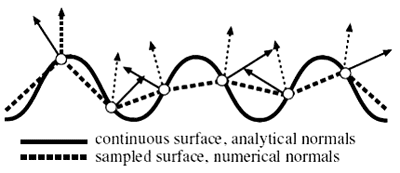
如图所示，取决于顶点的细节程度，分析方法比有限差分方法能计算出 更准确的法线。

自适应水面网格是优化水的渲染的一个好办法，但它们是复杂的，应用时需要认真考虑。

发布时间：2009/4/21 下午4:47:00  阅读次数：7610