第十节  磁场对运动电荷的作用力

我们知道，磁场对电流有作用力，既然电流是电荷的运动产生的，我们自然会想到，磁场力可能是直接作用在运动电上的。作用在整个导线上的安培力，不过是作用在运动电荷上的力的宏观表现。

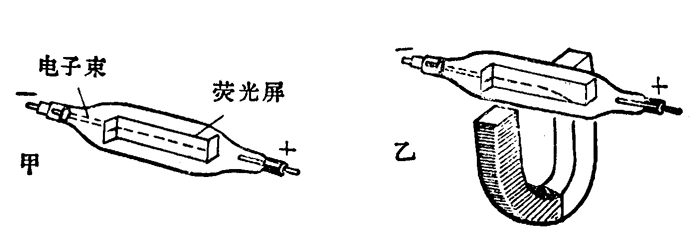
现在用实验来检验这个想法。图 1–34 是一个电子射线管，从阴极发射出来的电子束，在阴极和阳极间的高电压作用下，轰击到荧光屏上激发出荧光，我们就可以看到电子束运动的径迹。实验表明，在没有外磁场时电子束是沿直线前进的（图甲），如果把射线管放在蹄形磁铁的两极间，从荧光屏上可以看到电子束运动的径迹发生了弯曲（图乙）。这表明运动电荷确实受到了磁场的作用力，磁场对运动电荷的作用力通常叫做洛仑兹力。

洛仑兹力的方向也可以用左手定则来判定：伸开左手，让磁力线进入手心，四指指向正电荷运动的方向，那么拇指所指的方向就是正电荷所受的洛仑兹力的方向，运动的负电荷在磁场中所受的洛仑兹力，方向跟正电荷相反。洛仑兹力的大小可以从磁场对电流的作用力计算出来。设导线中单位体积内含有的运动电荷数是 n，每个电荷的电量是 q，电荷的平均定向移动速率是 v，导线的横截面积是 S，那么，通过导线的电流强度就是

I = nqvS

磁场对电流的作用力是 F = IlB sinθ。这个力可以看作是作用在每个运动电荷上的洛仑兹力的合力。设洛仑兹力为 f，这段导线内运动电荷的总数为 N，则 Nf = F，即 Nf = IlB sinθ，代入 I = nqvS，得到

Nf = nqvSlB sinθ

导线中运动电荷总数 N，等于单位体积内的运动电荷数 n 跟体积 Sl 的乘积，即 N = nSl，因此上式简化为

f = qvB sinθ

这就是说，洛仑兹力的大小等于电荷的电量 q、电荷的速率 v，磁感应强度 B 以及 v 和 B 间的夹角 θ 的正弦 sinθ 的乘积。在国际单位制中，上式中的各个物理量分别用牛顿、库仑、米／秒、特斯拉作单位。

当 θ = 90° 时，即电荷的运动方向跟磁场方向垂直时，电荷所受的洛仑兹力最大，等于 qvB。当 θ = 0 时，即电荷的运动方向跟磁场方向一致时，电荷所受的洛仑兹力最小，等于零。当 θ 角为其他数值时，洛仑兹力的大小在最大值和最小值之间。

练习六

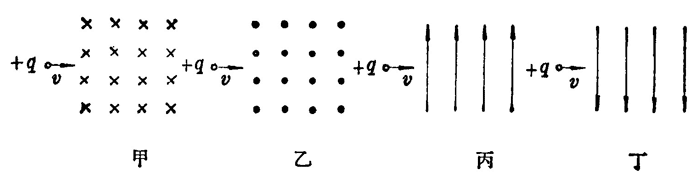
（1）如图 1–35 所示，带电粒子以速率 v 射入匀强磁场。分别标出带电粒子所受洛仑兹力的方向。

（2）一个带电粒子在空间中运动时没有发生偏转，能不能说明这个空间中没有磁场？为什么？

（3）一个电子以速率 v 射入磁感应强度为 B 的匀强磁场中，电子沿什么方向射入，受到的洛仑兹力最大？最大值是多大？沿什么方向射入，不受洛仑兹力作用？

（4）电子的速率 v = 3.0×10⁸ m/s，垂直射入 B = 0.1 特的磁场中，它受到的洛仑兹力是多大？

（5）一个电子以 1.2×10⁷ m/s 的速率射入磁感应强度为 0.02 特的匀强磁场中。当速率 v 与磁感应强度 B 的夹角 θ 为 30° 和 60° 时，电子所受洛仑兹力分别是多大？

（6）一电荷 q 在某一匀强磁场中运动，判断下面几种说法是否正确，并说明理由。

①只要速度的大小相同，所受的洛仑兹力就相同。

②如果速度不变，把电荷 q 改为 − q，洛仑兹力的方向将反向，但大小不变。

③如果速度不变，把 B 改为反向，洛仑兹力的方向将反向，但大小不变。

发布时间：2024/7/26 上午11:10:22  阅读次数：189