力的分解应根据实际产生的效果进行

有这样一个问题：用绳子悬挂着的物体，在水平面内作匀速圆周运动，问绳的张力有多大？解答有两种不同的结果。一种是：

Tcosθ－P＝0

T＝P/cosθ

另一种是：

Pcosθ－T＝0

T＝Pcosθ

前者认为物体在重力方向上是平衡的，所以该方向上的合力等于零；后者则认为物体在悬绳方向上是平衡的，所以该方向的合力也等于零。哪一种解答是正确的？怎样去分析呢？

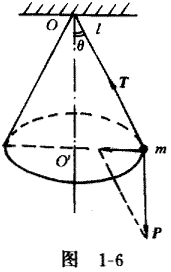首先分析物体的运动状态，因为物体是在水平面内作匀速圆周运动，所以它有一个向着中心O′的加速度，产生此加速度的力（向心力）显然只能是T和P的合力。从图1－6上不难看出合力的大小等于 Tsinθ＝Ptgθ，由此，可得到 T＝P/cosθ 的结果。

其次从力的分解方面去考虑，一般来说，求已知力的两个分力问题，如果没有附加条件，解答是不定的。在所讨论的圆锥摆中，重力P是已知的，求P的两个分力可有两种分解法：

一种是把重力P分解为沿悬线方向和垂直重力方向的两个分力如图1－7；另一种是把重力分解为沿悬线方向和垂直悬线方向的两个分力如图1－8。

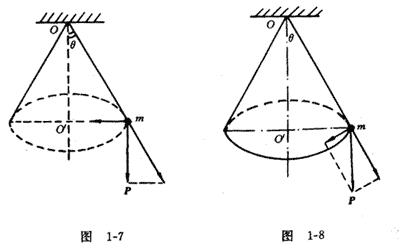
哪一种分解法符合实际呢？这就要从重力P产生的实际效果去分析了。题目明确指出，物体在水平面内作匀速圆周运动，那么重力P就只能产生两种效果：使悬线张紧和使物体在水平面作变加速运动，因而前一种分解是符合实际的。由此也可以得到T＝P/cosθ的正确结果。而第二种分解法，实际上是把圆锥摆的问题误解为单摆的问题了，这是经常容易混淆的问题。

2024 年按：此观点现在已经有点过时了。

发布时间：2009/4/13 下午1:56:58  阅读次数：9600