第二章 数学知识

2.1 简介

在生活中你可以看到许多不同种类的水并希望它们足够真实。自然界中不同类型的水有几个共同的特性，但有些特性截然不同。水的主要特性是：

• 水表面的反射
• 水面下的折射
• 多次反射和折射
• 反射和折射的比例：菲涅尔公式
• 一些颜色的小变化（脏水），水雾
• 水面的移动
• 镜面反射
• 深层水现象

2.2 水面的光学效果

2.2.1 反射

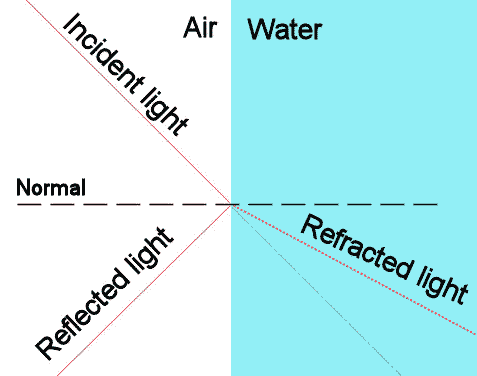
根据维基百科的定义：“反射是指波在两个不同介质之间发生的方向改变。常见的例子包括光线，声音和波浪的反射。”从某种程度上说水面就像一面镜子。光会在水面发生反射。物理规律是：反射角等于入射角，我们根据表面的法线测量这两个角度，即α＝β：

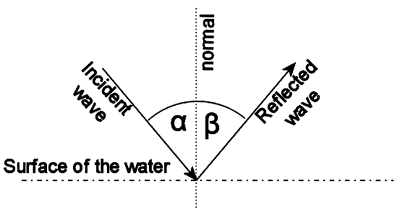
只考虑水面的反射很容易计算水面像素的颜色。将相机的位置关于水表面镜像：只需确定通过水面的每个像素的物体颜色就可以了，原理如图2-2所示：

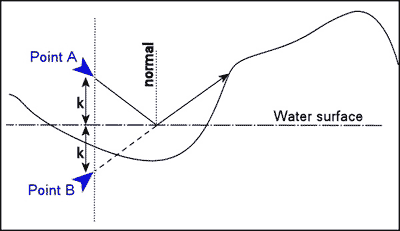
如果相机在A点，水面的颜色就是物体通过B点的交点的颜色。B点离开水面的距离与A点相同，这两个距离用图中的字母“k”表示。

2.2.2 折射

电磁波的速度在不同媒质中是不同的。光从一个介质通过另一个介质时速度会发生改变，这时会发生折射现象。根据斯涅耳定律（得名于荷兰数学家Willebrord Snellius），入射角和折射角之间的关系是：它们的比值是一个常数，取决于介质，更确切地说两者的正弦之比等于两介质中的波速之比：

sinθ₁/sinθ₂ ＝v₁/v₂ ＝n₂/n₁

或

n₁sinθ₁＝n₂sinθ₂

这两个角度是相对于界面法线的说的。根据这个规律，入射光会发生偏折，偏折程度由两介质的相对折射率决定。如图2－3所示：

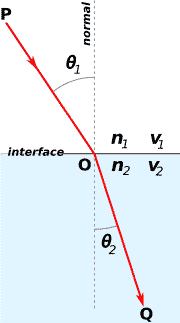
空气中的折射率为1，而水中为4/3。

2.2.3 三维空间

前面讨论的规律和例子只在2维平面中，但要描述现实世界，一切都需要三维。 [ MFGD ]提出了下列方程。s为入射光（向量），t是经过变换的光线，n为表面法线。转换的向量t有两个分量：一个平行于法线，另一个垂直于法线，可写成下列形式：

t = -n cosθ₂ + msinθ₂

要计算两个系数，我们需要用到这样一个关系：即只有沿表面的角会发生变化而不是整个方向都变化。m可以定义如下：

m = perp_ns / sinθ₁ = s - (n·s) n / sinθ₁

由前面的方程[ MFGD ]结果如下：

\[{\bf{t}} = - {\bf{n}}\left( {\sqrt {1 - \frac{{\eta _1^2}}{{\eta _2^2}}(1 - {{({\bf{n}} \cdot {\bf{s}})}^2})} + \frac{{{\eta _1}}}{{{\eta _2}}}({\bf{n}} \cdot {\bf{s}})} \right) - {\bf{s}}\frac{{{\eta _1}}}{{{\eta _2}}}\]

该方程中有可能包含负的平方根，这意味着方程的每个系数并不确定，物理原因如下描述。

2.3.4 临界角

我要提及的一个重要现象与折射有关。如果光线从光密媒质射向光疏媒质，折射角会变大，当入射角增至某一数值时，折射角等于90度，这时，折射光线消失，这种现象称为全反射，对应的这个入射角叫做全反射临界角，水射向空气的临界角约为50度。见图2－4：

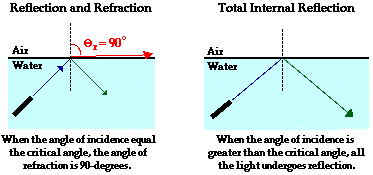
上面的图片来着维基百科和和

http://www.glenbrook.k12.il.us。

还有一个的Flash游戏可以理解反射和折射，在这个网址：

http://www.ps.missouri.edu/rickspage/refract/refraction.html

译者：以上知识可参见《新概念物理－光学》6至14页

2.2.5 多次反射和折射

光线在水面会发生反射和折射，但一定程度上光线会在表面再次反射和折射，图2－5说明了这种情况：

图像来自于[ TEoNIaRT ]。

2.2.6 反射和折射的比例：菲涅尔效果

译者注：对水面来说，当观察者和水面的角度越小时，反射效果越明显，角度越大时，折射效果越明显，称为菲涅尔效果。

本章的前两节介绍了反射和折射，它们在界面上是同时发生的，如图2-6所示：

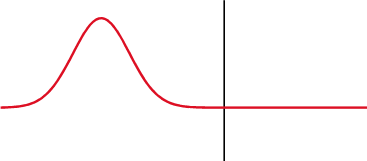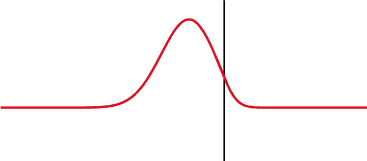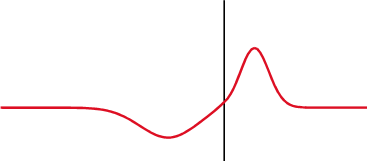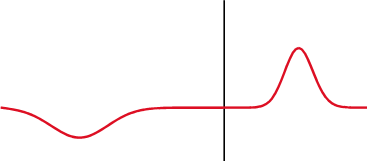
但是，如何获取准确的反射和折射的比例？Augustin-Jean Fresnel 在19世纪初得出了规律。他的方程用不同的强度定义了反射角和边界上的透光率，方程的导出过程已经超出本教程的范围。波有两个偏振分量：一个平行一个垂直。E_i是入射波振幅，E_r和E_t 是反射波的振幅和透射波的振幅。

r = E_r/E_i

t = E_t/E_i

垂直部分的方程如下：

r = (n_icosθ_i− n_tcosθ_t)/(n_icosθ_i + n_tcosθ_t)

t =2n_icosθ_i)/(n_icosθ_i+ n_tcosθ_t)

下一个方程显示的平行部分：

r = (n_icosθ_i− n_tcosθ_i)/(n_icosθ_t + n_tcosθ_i)

t = 2n_icosθi/(n_icosθ_t + n_tcosθ_i)

更优雅的版本有：

perpendicular r = −(sinθ_i−sinθ_t)/(sinθ_i+sinθ_t)

和

parallel r =(tanθ_i−tanθ_t)/(tanθ_i+tanθ_t)

如果光的偏振只有垂直部分，我们称之为S 极化。同样地，如果只有平行部分，称之为P极化。图2－7展示了取决于角度的系数在同时存在S 极化和P极化下的情况：

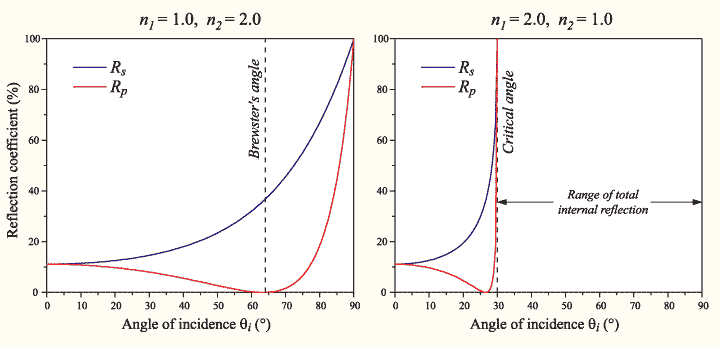
http://en.wikipedia.org/wiki/Fresnel_term

http://hyperphysics.phy-astr.gsu.edu/Hbase/phyopt/freseq.html

http://www.inyourfacefotos.com/fresnel.htm

译者：以上知识可参见《新概念物理－光学》276至288页

2．3水的移动

2.3.1 波

描述海浪是一个巨大的挑战。它有几个不同的部分并组合在一起形成一个非常复杂的系统。有两种不同类型的机械波：横波和和纵波。横波的中质点的振动方向与波的传播方向垂直，如图2－8所示：

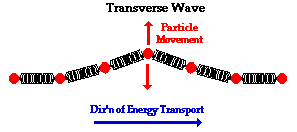
而纵波中质点的振动方向与波的传播方向在一直线，如图2－9所示：

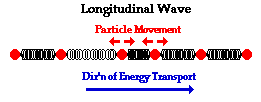
例如，声波在空气中的传播是纵波而弹吉他弦是横波。对于两种波来说，振幅是偏离平衡位置的最大位移，而波长是运动情况总相同的两质点间的最短距离。频率表示一秒内质点的振动次数，从以上数据很容易计算波速：波速等于频率乘以波长。

风和重力的共同作用构成了海浪沿表面的传播。这个复合系统既有横波又有纵波，使水粒子沿着一个圆形路径运动。越接近表面的粒子运动半径越大。这种波称为表面波，可用图2－10表示：

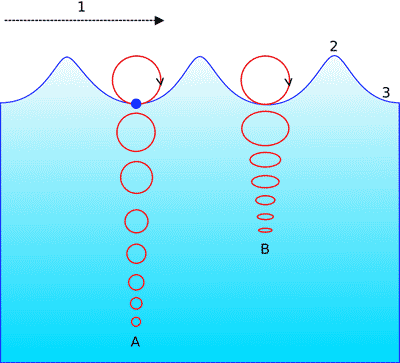
A点水较深，是圆形路径，B点水较浅，运动路径随着深度的增大变成椭圆并越来越扁。箭头＃1表示波的传播方向。＃2表示波峰，＃3表示波谷。下面的动画显示了这个过程：

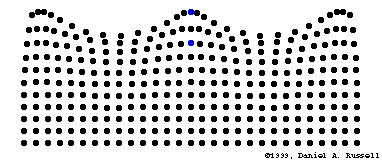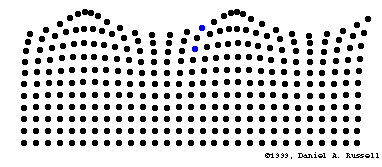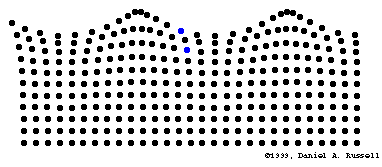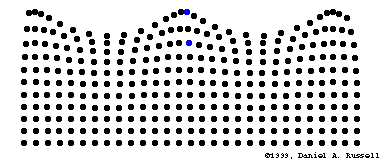
以下公式描述了表面波的散射关系（来自scienceworld homepage）：

\[{\omega ^2} = gk + \frac{{\gamma {k^3}}}{\rho }\]

ω是角频率，g是重力加速度，k是波数，γ是表面张力，ρ是密度。可用下式求ω：

\[\omega = \sqrt {gk + \frac{{\gamma {k^3}}}{\rho }} \]

2.3.2 复合系统－不同波的合成

先前讨论的理论足以描述海浪的运动，但我们需要使用更多具有不同振幅和波长的波获得更为真实的效果，如图2－11：

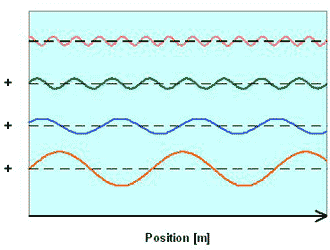
不同的波组合在一起形成如图2－12所示的波：

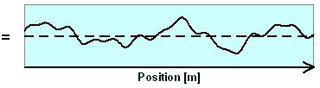
在三维世界中波的不同组成部分不仅有不同的振幅和波长，还有不同的传播方向。占主导地位的方向是最大幅度和最长周期的那个波。图2－13展示了三个组成部分：

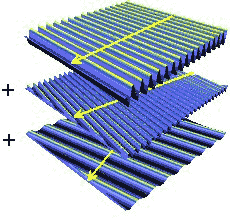
三者的组合可以近似的模拟真实的海表，如图2－14：

图片来自于 http://www.glenbrook.k12.il.us/gbssci/phys/Class/waves/u10l1c.html

和

http://www.carbontrust.co.uk/technology/technologyaccelerator/ME_guide2.htm

有用的链接：

http://oceanworld.tamu.edu/resources/ocng_textbook/chapter16/chapter16_01.htm

2.3.3 Gerstner波

捷克科学家Jozef Gerstner在1802年第一次提出了精确描述水波任意幅度的解决方法。他的模型还介绍了表面波的摆线运动。在这个模型中，水深比波长大。这个曲线也称为摆线。偏移量是由下列方程决定的：

x = X₀-(k/k₀) * A sin( k * X₀ - ωt)

y = A cos( k * X₀ - ωt)

公式中X₀是不受干扰的表面上的点，A是振幅，k是波矢，k₀是其大小。如果振幅很小，Gerstner波接近正弦，但如果振幅很大波会破碎，见图2－15：

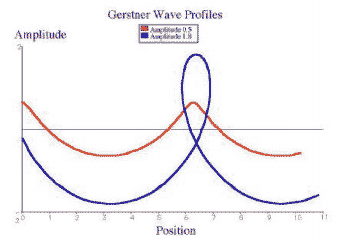
这些性质使Gerstner波可以用来描述不同情况下的波。更多细节可参见 [IAoOW] 或[GW]。

2.3.3 纳维－斯托克斯（Navier-Stokes）方程

Navier - Stokes方程（NSE）是非线性偏微分方程，用来描述的不可压缩的液体的运动。在NSE中有三个力：

• 重力：F_g＝ρG ，其中ρ是密度和G是引力（9.81 m/s²）。
• 压力：压力指向水面的法线。
• 粘滞力：水之间的摩擦力，作用在水的各个方向上。

公式中的时间t依赖于混沌，流体的随机行为称为动荡，Navier - Stokes方程用来描述这个现象，但现在还没有解决这个方程的求解。谁能作出初步的数学理论将有助于理解这种现象，奖金是100万美元。Navier - Stokes方程如下：

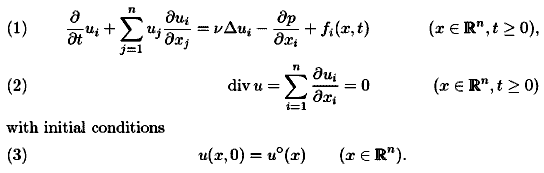
uº(x)给定，C∞divergence-free矢量场Rn上，fi(x, t)是给定的分量，外加力（如重力），ν是粘滞系数，

\[\Delta = \sum\limits_{i = 1}^n {\frac{{{\partial ^2}}}{{\partial x_i^2}}} \]

是拉普拉斯算符。欲了解详情，请参阅[ NSEP ]或[ GPUGEMS ]。

译者：这个公式十分眼熟，原来在几个月前看的一本名叫《千年难题》书中见过。此书描述了七大“悬赏一百万美元的难题”，从简到难分别是：黎曼假设，杨－米尔斯理论和质量缺口假设，P对NP问题，纳维－斯托克斯方程，庞加莱猜想，戴尔猜想，霍奇猜想。纳维－斯托克斯方程排第四，纳维是法国当时最著名的工程师之一，他的名字被刻在了埃菲尔铁塔上。纳维改进了欧拉的方程，使之能适用于有一定黏性的流体这一更为实际的情况。纳维的数学推理是有缺陷的。但由于运气好（或者说由于工程师的过人直觉），他最后得出的方程是正确的。几年之后，爱尔兰数学家斯托克斯（在月亮和火星上都有以他名字命名的环形山）作出了正确的推导。但没有人能够找出一个解纳维－斯托克斯方程的公式。确切地说，没有人能够在原则上证明这个方程是否有解！（当然，每当一种真实的流体作了一次流动，大自然就“解”了一次这个方程）

2.4各种水现象

2.4.1镜面反射

具有一个平面的材料（如：皮革，玻璃和水）有一个有趣的现象，这点我前面没有提及。有几种不同的反射模式，其中一些模式使图像更加逼真，同时也有助于改近小的细节。其中一个是镜面反射。像沙子之类的材料有不规则，不平坦的表面，这使得入射光在每一个方向都会反射。图2－16表示了这个现象：

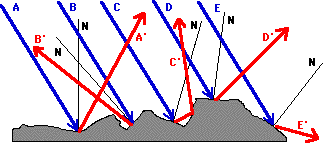
但是，如果材料具有光滑表面，入射光将会平行反射。由于这个性质，如果入射光从特定角度入射的话，会在皮革、不同的金属或水之类的物体上形成光泽和亮点。Phong光照模型是三维图形中最常用的方式。Phong Bui Tong在1975年提出了这个模型至今仍使用得很普遍。根据这个模型，点的亮度有三个组成部分：一个环境光，一个漫反射光和一个镜面反射光。如果观察者远离反射光的方向，那么镜面反射将变弱。图2－17显示了相关的矢量：

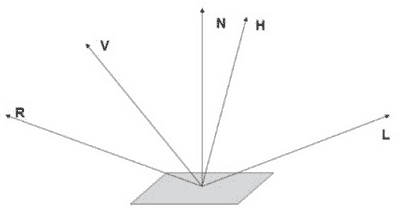
在Phong模型中，反射强度近似为角度余弦的幂，原始公式是：

k_spec cosⁿβ

其中β是R和V的夹角，k_spec是镜面反射系数。指数n可以影响锐度的大小，指数越大反射越强。两个向量的点乘等于它们之间的角度的余弦，所以公式可以写成：

k_spec (V•N)ⁿ

这里的“ • ”表示点乘。使用漫反射光照模型Phong光照模型如下表示（I是指强度）：

I = k_ambient * I_ambient + (Ip /(d)) [k_diffuse * (N•L) + k_specular * (V•R)ⁿ]

k是环境、漫反射、镜面反射系数，“ • ”指点乘，即点的光强等于三者的和。

http://www.dgp.toronto.edu/~karan/courses/csc418/fall_2002/notes/illum_local.html

http://www.mini.pw.edu.pl/~kotowski/Grafika/IlluminationModel/Index.html

2.4.2 刻蚀（Caustics）

水面还有刻蚀：光束从弯曲的表面反射或折射，因此只聚焦在受光面上的某些区域，于是就产生了刻蚀现象，如图2－18所示：

刻蚀的原理如图2－19所示

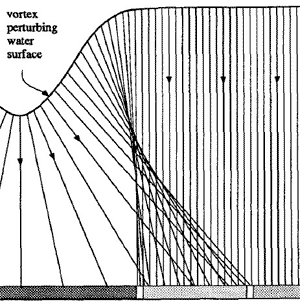
2.4.3 Godrays

引起刻蚀的相同物理效果也会形成Godrays（在[ DWAaR ]中提及）。不断变化的水面使光线不断聚焦和失焦。水中漂浮的小颗粒可以进入这些焦点中，并在短期内可见。由这些效果产生的光斑不断变化被称为Godrays，如果您从水下看光源就可以看到这种现象。图2－20是一个渲染的例子：

2.4.4 白浪和泡沫（Whitecaps and foam））

波浪的破碎会形成泡沫，堆积的部分叫做白浪。根据[ RNW ]，白浪取决于水的温度和水面上空气的化学性质。他们使用一个经验公式来近似覆盖泡沫的水的光学特性：

f = 1.59 * 10^-5 U^2.55 exp[0.086 * (T_w - T_a )]

其中f是小数部分，U是风速，T_W和T_a是水和空气摄氏温度。

2.4.5 开尔文水楔（The Kelvin Wedge）

在开放的水域，移动的船只会产生波浪。这些波浪不能视为纵波。这种现象，称之为水楔，首先是由开尔文勋爵提出的。一个理想化的例子可见图2－21

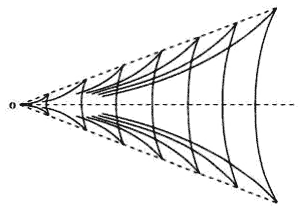
船只后面的复杂波形受到水的粘度、移动方向、重力的影响，如果振幅很大，还要产生非线性俄效果。Stern波和涡流互相叠加，and not infrequently, other wave systems may be discerned originating from somewhere between the bow and stern。事实上，与船的速度无关，该角有开尔文水楔封闭，解释这个超出了本文的范围。详细信息请参阅[ FDfP ]。

参考资料

[MFGD] - Mathematics for Game Developers - Christopher Tremblay - Thomson course technology.

[DWAaR] - http://www.gamasutra.com/gdce/2001/jensen/jensen_04.htm，Deep-Water Animation and Rendering

[TEoNIaRT] -http://delivery.acm.org/10.1145/1110000/1103932/cs31.pdf?key1=1103932&key2=1886155021&coll=GUIDE&dl=GUIDE&CFID=59177333&CFTOKEN=24688997，The elements of nature: interactive and realisic techniques

[RNW] - http://www.cs.utah.edu/vissim/papers/water/waterColorPG.pdf，Rendering Natural Waters - Simon Premoze, Michael Ashikhmin

[TYPHOON] - http://www.gameprog.it/hosted/typhoon/water.htm，Typhoon 3D engine

[NSEP] - http://www.claymath.org/millennium/Navier-Stokes_Equations/navierstokes.pdf，CHARLES L. FEFFERMAN: Existence and smoothness of the Navier-Stokes equation

[GPUGEMS] - http://developer.download.nvidia.com/books/HTML/gpugems/gpugems_ch38.html，Gpu Gems - Chapter 38. : Mark J. Harris: Fast Fluid Dynamics Simulation on the GPU

[FDfP] -http://books.google.hu/books?id=9LaWEx4XbvYC&pg=PA188&lpg=PA188&dq=kelvin+ship+waves&source=web&ots=-h_cO-AtAy&sig=7uoGo8atyiDN2V7XmsUUShJOmU8&hl=en#PPA188,M1"，T. E. Faber: Fluid Dynamics for Physicists

[IAoOW] -http://www-evasion.imag.fr/Publications/2002/HNC02/wavesSCA.pdf，Damien Hinsinger, Fabrice Neyret, Marie-Paule Cani: Interactive Animation of Ocean Waves

[GW] - Jefrey Alcantara ，http://www-viz.tamu.edu/students/jd/658/T_algorithms.html

发布时间：2009/4/9 下午4:33:08  阅读次数：12674