是合力为零还是没有合力？

在物体的受力分析中，常常会听到“合力为零”和“没有合力”这样的力学术语。“合力为零”与“没有合力”是否是一回事？下面我们就一具体例子来加以说明。

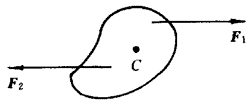
如图所示，一放在光滑水平面上的刚体受到了一力偶（F₁，F₂）的作用，刚体质心为C。试问，作用在刚体上的合力情况如何？

好多人认为，刚体在竖直方向处于平衡状态，水平方向又仅受一力偶作用，故作用在刚体上的合力为零。其实这样说法是不妥的，甚至是错误的。要说明此问题，只需让我们回忆一下合力的定义即可。定义说：“如果一个单力作用在物体上所产生的效果跟几个力同时作用的效果相同。这个单力就叫做那几个力的合力，而那几个力就叫做这个单力的分力”。

从上述定义可知，所谓“合力”完全是一个“等效”概念，即“合力”是以一个“等效”的单力来定义的。这里的等效实际上应包括受力对象不变，力的性质不变和力的作用效果不变，而其中以力的作用效果不变尤为重要。力的作用效果又应分为平动效果、转动效果和形变效果三种。对于刚体而言，第三种形变效果可不予考虑。

对照题设刚体，不难知道，在一力偶作用下，它将只作平面转动，或者说力偶对刚体只有转动的作用效果。那么，根据合力的定义，设想有哪一个单力作用在此刚体上而能使刚体只产生同样转动的效果呢？显然，此力是不存在的。原因是单个力作用在刚体（除质心外）上既要产生平动效果又要产生转动效果。力偶是一个特殊力系，在任何情况下，它都不能与一个单力等效，也不能被一个单力平衡。理论力学中，类似的问题也只是称“主矢量为零”，“主力矩不为零”，而决不是说“合力为零”的。认为“合力为零”，事实上已承认了合力的存在，因为如上所述，合力概念在实质上代表的是一个单力。既然是单力，它就应该满足力的三要素，即具有大小、方向和确定的作用点。“合力为零”实质上就是“等效单力”，只是大小为零、方向任意而作用点仍是确定的。然而，这里刚体所受力偶（F₁，F₂）的矢量和ΣF＝F₁＋F₂＝0，并不满足力的三要素，它只有大小和方向，是符合矢量运算规则的合矢量，但它没有确定的作用点 。所以对上例正确的说法是此时不存在合力或没有合力。

由此可见，“合力为零”与“没有合力”粗看起来是属于同一个力学术语，但实际上应属于两个不同的力学概念。没有合力（不存在合力）并非合力为零！

发布时间：2009/4/7 上午7:10:35  阅读次数：14929