7.11 康普顿效应

在 1923 年 5 月的《物理评论》上，A.H.康普顿发表了题为《X 射线受轻元素散射的量子理论》的论文，文中用光量子假说对后来以他的名字命名的效应作出解释。他写道：

“从量子论的观点看，可以假设：任一特殊的 X 射线量子不是被辐射器中所有电子散射，而是把它的全部能量耗于某个特殊的电子，这电子转过来又将射线向某一特殊的方向散射，这个方向与入射束成某个角度。辐射量子路径的弯折引起动量发生变化。结果，散射电子以一等于 X 射线动量变化的动量反冲。散射射线的能量等于入射射线的能量减去散射电子反冲的动能。由于散射射线应是一完整的量子，其频率也将和能量同比例地减小。因此，根据量子理论，我们可以期待散射射线的波长比入射射线大”，而“散射辐射的强度在原始 X 射线的前进方向要比反方向大，正如实验测得的那样。”[1]

康普顿用图 7 – 21 解释射线方向和强度的分布，根据能量守恒和动量守恒，考虑到相对论效应，得散射波长为

\[{\lambda _\theta } = {\lambda _0} + \left( {\frac{{2h}}{{mc}}} \right){\sin ^2}\frac{\theta }{2}\]

即波长的改变量

\[\Delta \lambda  = {\lambda _\theta } - {\lambda _0} = \left( {\frac{{2h}}{{mc}}} \right){\sin ^2}\frac{\theta }{2}\tag{7-8}\label{7-8}\]

Δλ 为入射波长 λ₀ 与散射波长 λ_θ 之差，h 为普朗克常数，c 为光速，m 为电子的静止质量，θ 为散射角。

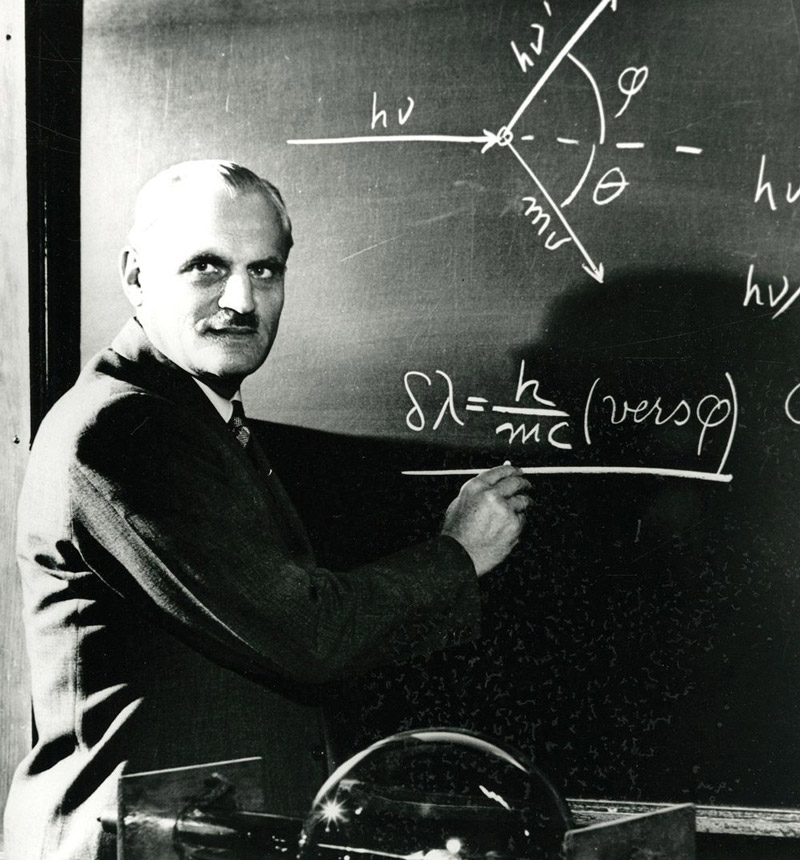
这一简单的推理对于现代物理学家来说早已成为普通常识，可是，康普顿却是得来不易的。这类现象的研究历经了一二十年才在 1923 年得出正确结果，而康普顿自己也走了 5 年的弯路，这段历史从一个侧面说明了现代物理学产生和发展的不平坦历程。

从式（7 – 8）可知，射线波长的改变决定于 θ，与 λ₀ 无关，即对于某一角度，波长改变的绝对值是一定的。入射射线的波长越小，波长变化的相对值就越大。所以，康普顿效应对 γ 射线要比 X 射线显著。历史正是这样，早在 1904 年，英国物理学家伊夫（A.S.Eve）就在研究 γ 射线的吸收和散射性质时，首先发现了康普顿效应的迹象。他的装置如图 7 – 22。图中辐射物和吸收物实际上是铁板、铝板之类的材料，镭管发出 γ 射线，经散射物散射后投向静电计。在入射射线或散射射线的途中插一吸收物以检验其穿透力。伊夫发现，散射后的射线往往比入射射线要“软”些。[2]

后来，γ 射线的散射问题经过多人研究，英国的弗罗兰斯（D.C.H.Florance）在 1910 年获得了明确结论，证明散射后的二次射线决定于散射角度，与散射物的材料无关，而且散射角越大，吸收系数也越大。所谓射线变软，实际上就是射线的波长变长，当时尚未判明 γ 射线的本质，只好根据实验现象来表示。

1913 年，麦克基尔大学的格雷（J.A.Gray）又重做 γ 射线实验，证实了弗罗兰斯的结论并进一步精确测量了射线强度。他发现：“单色的 γ 射线被散射后，性质会有所变化。散射角越大，散射射线就越软。”[3]

实验事实明确地摆在物理学家面前，可就是找不到正确的解释。

1919 年康普顿也接触到 γ 散射问题。他以精确的手段测定了 γ 射线的波长，确定了散射后波长变长的事实。后来，他又从 γ 射线散射转移到 X 射线散射。图 7 – 23 是康普顿自制的 X 射线分光计，钼的 K_α 线经石墨晶体散射后，用游离室测量不同方位的散射强度。

图 7 – 25 是康谱顿发表的部分曲线。从图中可以看出，X 射线散射曲线明显地有两个峰值，其中一个波长等于原始射线的波长（不变线），另一个波长变长（变线），变线对不变线的偏离随散射角变化，散射角越大，偏离也越大。

查外文资料发现原图中的横坐标单位可能标错了

遗憾的是，康普顿为了解释这一现象，也和其他人一样，走了不少弯路。

他开始是用 J.J.汤姆孙的电子散射理论解释 γ 射线和 X 射线的散射，后来又提出荧光辐射理论和大电子模型。他设想电子具有一定的大小和形状，认为只要“电子的电荷分布区域的半径与 γ 射线的波长大小可比拟”就可以“在经典电动力学的基础上解释高频辐射的散射。”他为了解释荧光辐射的频率变低，曾试图用多普勒效应进行计算，在计算中，他把 X 射线对散射物质中电子的作用看成是一个量子过程。开始他用能量 hν = \(\frac{1}{2}\)mv² 进行计算，结果与实际不符。后来，他终于采用了两个条件，在碰撞中既要遵守能量守恒，又要遵守动量守恒，从而，导致了 1923 年 5 月在《物理评论》上发表了那篇有历史意义的文献。

接着，德拜也发表了早已准备好的论文。他们两人的论文引起了强烈反响。然而，这一发现并没有立即被科学界普遍承认，一场激烈的争论迅即在学术界中展开。这件事发生在 1922 年以后，一份内有康普顿关于 X 射线散射的报告在交付出版之前，先要经美国研究委员会的物理科学部所属的一个委员会讨论。他是这个委员会的成员。可是，这个委员会的主席杜安（W.Duane）却极力反对把康普顿的工作写进去，认为实验结果不可靠。因为杜安的实验室也在做同样的实验，却得不到同样的结果。双方展开了激烈的论战。

康普顿的学生，从中国赴美留学的吴有训（1897—1977）对康普顿效应的进一步研究和检验作出过重大贡献，除了针对杜安的否定作了许多有说服力的实验外，还证实了康普顿效应的普遍性。他测试了多种元素对 X 射线的散射曲线，结果都满足康普顿的量子散射公式（7 – 8）。图 7 – 26 就是康普顿和吴有训 1924 年发表的曲线，他们的论文题目是：《被轻元素散射时钼 K_α 线的波长》。文中写道：“这张图的重要点在于：从各种材料所得之谱在性质上几乎完全一致。每种情况，不变线 P 都出现在与荧光 M₀K_α 线（钼的 K_α 谱线）相同之处，而变线的峰值，则在允许的实验误差范围内，出现在上述的波长变化量子公式所预计的位置 M 上。”[4]

爱因斯坦在肯定康普顿效应中起了特别重要的作用。前面已经提到，1916 年爱因斯坦进一步发展了光量子理论。根据他的建议，玻特和盖革（Geiger）也曾试图用实验检验经典理论和光量子理论谁对谁非，但没有成功。当 1923 年爱因斯坦得知康普顿的结果时，他热忱地宣传和赞扬康普顿的发现，多次在会议和报刊上提到它的重要意义。例如，1924 年 4 月 20 日在《柏林日报》副刊上发表题为“康普顿的实验”的文章，文中写道：

“我想在下面对涉及光或电磁辐射的一个重要实验的讨论中报导大约一年以前美国物理学家康普顿做的实验。为了全面认识这一实验的意义，我们必须了解此刻辐射理论正处于高度显要的地位。”

爱因斯坦全面论述了光的微粒理论和波动理论的发展历史。他从牛顿的微粒说或发射说一直讲到普朗克的量子假说。他讲到麦克斯韦的理论无法解决热辐射定律，然后写道：

“对普遍理论的失败所作的解答是提出光量子假说。尽管波动理论具有普遍性，这一工作假说还是有根据的，因为辐射是属于一种能量联系行为，就好像它是由能量投射体组成的，其能量仅仅决定于辐射的频率（颜色）并与频率成正比。牛顿的光的微粒理论又重新复活，尽管它在光的基本波动特性领域内完全是失败的。”

“所以，现在有两种关于光的理论，全都是不可缺少的，而且没有任何逻辑联系虽然经过理论物理学家们的二十年的巨大努力，我们今天还必须予以承认。量子理论还使玻尔的原子理论成为可能，并且解释那么多事实，以至于它包括了大量的真理。考虑到这些事实，思考把投射体的性质赋予光粒子或光量子究竟还应走多远，这该成为极其重要的问题了……”

“康普顿实验的正效果证明，辐射不但在能量传递方面，而且对于碰撞中的相互作用来说，辐射也表现得好像是由一些分立能量投射体所组成的一样。”[5]

正是由于爱因斯坦等人的努力，光的波粒二象性迅速获得了广泛的承认。

康普顿效应的历史意义可以从香克兰（R.S.Shankland）的评述得到说明：

“康普顿效应决定性地证明了，仅仅把经典的波动电动力学作某些修改，例如玻尔-克拉默斯-斯莱特建议的那样，是不能被人们接受的，而是辐射的波动性和粒子性两方面都必须得到承认。另一方面康普顿理论也是建立在旧量子论上的，它的预言也显示有重大的局限性，作为能量函数的总散射截面和作为角度函数的微分散射截面都不能精确地作出预言。还有其他的一些重要现象指引理论发生变革，不久新量子力学发展起来了，很快出现了许多新的结果。而康普顿效应确实在激励这一重大进展方面起了重要作用。因为它是辐射与物质相互间如此基本的相互作用，以至于任何可接受的理论都必须精密而正确地解释它的所有的特性。这一精密而正确的解释最终从新的量子力学获得的一些基本结果得到了。狄拉克的相对论性电子理论，包括了电子自旋效应，导出了康普顿散射截面的克莱因-仁科（Klein-Nishina）公式。更重要的是，狄拉克辐射场的量子化，对波动性和粒子性作了统一描述，这正是康普顿效应所要求的。再有，当温策尔（G.Wentzel）把这一理论用之于 X 射线受束缚电子散射时，就可以把变线和不变线全部解释清楚了。”[6]

光电效应和康普顿效应都为光的粒子性提供了令人信服的证据。然而，康普顿效应比光电效应更前进了一步，因为在解释康普顿效应时不但要考虑能量守恒，还要考虑动量守恒，由此为光的波粒二象性及德布罗意物质波假说提供了更完全的证据。美国科学史专家斯徒埃尔（Roger H.Stuewer）把康普顿效应与物理学的转折点联系在一起，是很有道理的。[7]

下面一章就来介绍从德布罗意物质波假说到量子力学的建立和发展的历史进程。

[1] Compton AH.Phys.Rev.，1923（21）：483

[2] Eve A S.Phil.Mag.，1904（8）：669

[3] Gray J A.Phil.Mag.，1913（26）：611

[4] Compton A H，Woo Y H.Proc.Nat，Acad.Sci，1924（10）：27

[5] Shankland R S，ed.Scientific Papers of A.H.Compton.Univ.of Chicago Press，1973

[6] 转引自：郭变玲，沈慧君.吴有训的科学贡献.鹭江出版社，1997.108

[7] Roger H Stuewer.The Compton Effect-Turning Point of Physies.NewYork:Science History Publications，1975

发布时间：2024/3/4 下午3:14:05  阅读次数：3796