6.5 广义相对论的建立

6.5.1 狭义相对论的局限性

狭义相对论建立以后，爱因斯坦并没有止步。他认为狭义相对论还有许多问题没有解决。例如：为什么惯性坐标系在物理学中比其他坐标系更为优越？（马赫最先提出这个问题）为什么惯性质量随能量变化？为什么一切物体在引力场中下落都具有同样的加速度？刚刚经受住考验的狭义相对论，为什么一用到引力场中就遇到了矛盾？爱因斯坦感到极大的疑惑。他坚信自然界的和谐与统一，认为要么对惯性坐标系为什么会特别优越作出解释，要么放弃惯性坐标系的特殊优越地位。

1922 年，爱因斯坦在京都大学访问期间所作的《我如何创立相对论》的讲演中，讲道：

“我对广义相对论的最初想法出现在两年之后的 1907 年。思想是突然产生的。我对狭义相对论并不满意，因为它被严格地限制在一个相互具有恒定速度的参照系中，它不适用于一个做任意运动的参照系，于是我努力地把这一限制取消，以使这一理论能在更为一般的情况下讨论。”[1]

爱因斯坦坚信世界的内在和谐，他追求的是理论的逻辑统一，不能容许惯性系与非惯性系之间这种内在不对称性情况的存在。如何来解决这个难题呢？惟一的途径就是把狭义相对性原理扩大到非惯性系统。

狭义相对论面临的另一严重困难来自引力，因为它与牛顿的引力公式和引力势方程不相容。

自狭义相对论提出后，许多人曾致力于检验各种物理定律在洛伦兹变换下的协变性，他们都获得了成功，但是包括爱因斯坦本人在内，都发现当把牛顿的引力理论纳入到相对论理论之中时，却遇到了明显的矛盾。起初，爱因斯坦认为寻找一个描述引力场变化的结构定律也许并不难。他试图在狭义相对论的框架内处理引力定律，推出引力的场定律。他在 1933 年的演讲《广义相对论的来源》中讲道：

“最简单的做法当然是保留拉普拉斯的引力标量势，并且用一个关于时间的微分项，以明显的方式来补足泊松方程，使狭义相对论得到满足。引力场中质点的运动定律也必须适应狭义相对论。”[2]

可是，研究得到的结果却是，落体的加速度与它的内能有关，这引起了爱因斯坦的强烈怀疑。因为这样的结果不符合众所周知的实验事实：在引力场中一切物体都具有同一加速度。这一尝试使爱因斯坦在 1907 年认识到：在狭义相对论的框子里，不可能有令人满意的引力理论。

爱因斯坦 1922 年回忆他创建广义相对论的过程时讲道：当他正在思考如何突破狭义相对论的框架，以解决惯性与重量之间的不协调时，一个突然的闪念出现了。他说：“有一天，突破口突然找到了。当时我正坐在伯尔尼专利局办公室的椅子上，脑子里突然闪现了一个念头：如果一个人正在自由下落，他决不会感到他的重量。我吃了一惊。这个简单的思想实验给我的印象太深了。它把我引向了引力理论。我继续想下去：下落的人正在作加速运动，可是在这个加速参照系中，他有什么感觉？他如何判断面前所发生的事情？于是我决定把相对性理论推广到加速参照系。”[3]

爱因斯坦 1933 年在《广义相对论的来源》一文中，这样写道：“在引力场中一切物体都具有同一加速度，这条定律也可以表述为惯性质量与引力质量相等的定律，它当时就使我认识到它的全部重要性。我为它的存在感到极为惊奇，并猜想其中必定有一把可以更加深入地了解惯性和引力的钥匙。”[4]

爱因斯坦从古老的实验事实寻找到了解决这一难题的钥匙。这就是惯性质量与引力质量等价的实验结果。

6.5.2 惯性质量与引力质量的等价

质量有两个定义，一个反映惯性的大小，叫惯性质量，以符号 m_惯 表示，根据的是牛顿第二定律

\[F = {m_惯} \cdot a\]

式中 a 为力 F 作用下物体的加速度；另一个反映引力的大小，叫引力质量，以符号 m_引 表示，根据的是万有引力定律

\[F = {m_引} \cdot \frac{{GM}}{{{R^2}}}\]

式中 G 为引力常数，M 与 R 为地球的质量与半径，F 为物体所受地球的引力。对于地面上的自由落体运动，应有

\[{m_惯} \cdot a = {m_引} \cdot \frac{{GM}}{{{R^2}}}\]

这两个定义不同的质量，是否有一定的比例关系，这个问题在经典理论中得不到解答，只能靠实验作出判断。实验证明，它们之间有严格的比例关系。

最早的证据就是自由落体实验。从伽利略时代就知道自由落体的加速度相同，与物体的成分及轻重无关。考虑两个物体 A 和 B 同时下落，

对于物体 A，有                             m_惯A·a_A = m_引A·\(\frac{{GM}}{{{R^2}}}\)，

对于物体 B，有                              m_惯B·a_B = m_引B·\(\frac{{GM}}{{{R^2}}}\)，

既然 a_A = a_B 必有

\[\frac{{{m_{惯A}}}}{{{m_{引A}}}} = \frac{{{m_{惯B}}}}{{{m_{引B}}}} = 常数 \]

可见，惯性质量与引力质量成正比。

牛顿提出运动定律和万有引力定律时必然要碰到两种质量的关系问题。他亲自做了实验，用不同材料充当单摆的摆锤，比较它们的摆动周期。

摆长为 l 的单摆，振动周期为

\[T = 2\pi \sqrt {\frac{l}{g}}  \cdot \sqrt {\frac{{{m_惯}}}{{{m_引}}}} \]

如果实验证明，当 l 一定时振动周期 T 确为常数，与摆锤的成分无关，则 m_惯/m_引 应为常数。

牛顿用空心容器当作摆锤，里面分别放进重量精确相等的各种不同物质，例如：金、银、铅、玻璃、砂、食盐、木料、水和麦子等物。他写道：

“我做了两个一样的木盒。一个装满木材，另一个在摆动中心处挂上等量的金（尽可能准确）。两个盒子用 11 英尺（1 英尺 = 0.304 8 m）长的同样的线挂起来成为一对摆，它们的重量和形状完全一样，并同样地受到空气阻力。把两者挨着放，我观察到，它们长久地以同一频率一起来回摆动。因此，金里的物质的量与木料里物质的量之比同作用在全部金上的力与作用在全部木料上的力之比是相同的。”[5]

用数学形式表示，正是

\[\frac{{{m_{惯(金)}}}}{{{m_{惯(木)}}}} = \frac{{{m_{引(金)}}}}{{{m_{引(木)}}}}\]

即

\[\frac{{{m_{惯(金)}}}}{{{m_{引(金)}}}} = \frac{{{m_{惯(木)}}}}{{{m_{引(木)}}}}\]

既然这两种质量之比是常数，适当调整引力常数的数值，就可使 m_惯 = m_引，所以牛顿在创建经典力学的理论体系时，就不再区分惯性质量和引力质量了。

从实验方法来说，不论是自由落体实验，还是单摆实验，测量精度都不高，因为这两种实验都是动态的，涉及位置和状态的变化，会受其他因素，例如空气阻力的干扰。根据牛顿的记述，他的实验精度为千分之一。

我们可以引用参数 η（A，B）来代表两种质量的差异，定义

\[\eta (A,B) = \frac{{{{\left( {\frac{{{m_引}}}{{{m_惯}}}} \right)}_A} - {{\left( {\frac{{{m_引}}}{{{m_惯}}}} \right)}_B}}}{{\frac{1}{2}\left[ {{{\left( {\frac{{{m_引}}}{{{m_惯}}}} \right)}_A} + {{\left( {\frac{{{m_引}}}{{{m_惯}}}} \right)}_B}} \right]}}\]

对于牛顿的实验来说，η（A，B）< 1×10⁻³。

更精确的质量等价实验是匈牙利物理学家厄缶（Loránd Eӧtvӧs，1848—1919）在 1889 年做的。他采用扭秤方法，把动态实验改为静态实验，直接比较两个物体的惯性质量和引力质量，从而大大地提高了实验精度。

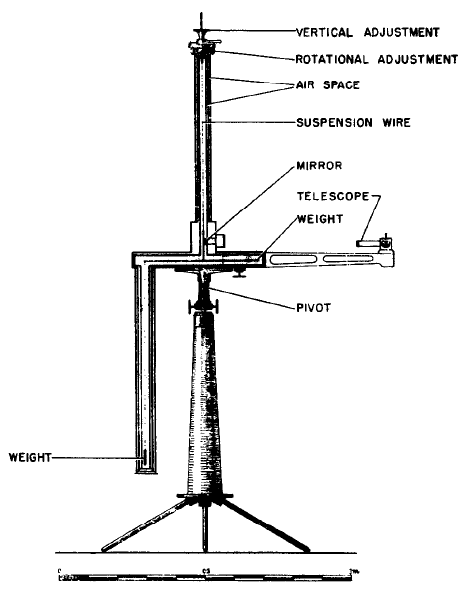
厄缶实验的原理如图 6 – 9 所示。

一根横杆悬挂在细线下，横杆两端对称地固定着不同材料但重量相同的重物 A 和 B。这两个重物都会受到重力 m_引·g 和地球自转造成的离心力 m_惯·ω²Rcosφ 的作用。其中 ω 是地球自转的角速度，φ 是地理纬度。如果惯性质量与引力质量等价，则两重物所受离心力相等，力矩互相抵消，扭秤维持平衡。如果惯性质量与引力质量不成正比，则扭秤失去平衡，而使悬丝扭转。

厄缶实验的原理虽然简单，但结果非常精确。和大多数精确的实验一样，这个实验也用示零法。装置如图 6 – 10，横杆长 40 cm，悬丝用铂铱合金。他用望远镜对准悬丝上挂着的小反射镜，观察望远镜上方的短刻度标尺，从而测量偏转角。从悬丝到刻度尺的距离为 62 cm。为了避免系统误差，厄缶还将横杆转 180°，换一个方向测量。1889 年得到第一次结果，平均为 η（A，B）< 5×10⁻⁸。1908 年得到第二次结果（直到 1922 年才正式发表，这时厄缶已经去世），实验精度达 η（A，B）< 2×10⁻⁹。这个实验是20世纪初最引人注目的经典实验之一。

6.5.3 作为广义相对论基础的两个基本公设

和构思狭义相对论构架的过程一样，爱因斯坦在构思广义相对论的基本公设时，也力图寻找已有的实验基础。他从这样一个基本事实出发，即在引力场中任一点，一切自由落体加速度相同，进而认识到引力场与参照系相当的加速度在物理上完全等效。

1907 年，爱因斯坦在他的《关于相对性原理和由此得出的结论》一文中首次提出两个基本原理。一个叫等效原理，或者叫等价原理，即：“引力场同参照系的相当的加速度在物理上完全等价。”另一个叫广义相对性原理，他写道：“迄今为止，我们只把相对性原理，即认为自然规律同参照系的状态无关这一假设应用于非加速参照系。是否可以设想，相对性运动原理对于相互作加速运动的参照系也依然成立？”[6]他假设可以用一个均匀加速的参照系来代替均匀引力场。值得注意的是，均匀加速的参照系并不是普遍的参照系。在 1913 年之前，爱因斯坦并没有明确地提出广义协变原理，而是认为应该有广义协变性。正是这种矛盾状态促使爱因斯坦做进一步深入的研究。到了 1916 年，爱因斯坦发表《广义相对论的基础》，这是关于广义相对论的第一篇完整的总结性论文，他明确提出：“物理学的定律必须具有这样的性质，它们对于以无论哪种方式运动着的参照系都是成立的。”[7]这就是推广了的相对性公设：“普遍的自然规律是由那些对一切坐标系都有效的方程来表示的，也就是说，它们对于无论哪种代换都是协变的（广义协变）。”[8]

两个基本原理：一个是等效原理，一个是广义协变原理，就成了爱因斯坦推广相对性理论的基本出发点。

6.5.4 时空柔性度规的创建

然而，跟狭义相对论的两条看来似乎矛盾的基本公设一样，广义相对论的两条基本原理也存在一定的矛盾。爱因斯坦为了克服这一困难，花了好几年的时间，希望寻到满意的解决办法。正如他在《自述》中说的：“其主要原因在于；要使人们从坐标必须具有直接度规意义这一观念中解放出来，可不是那么容易。”[9]

所谓直接度规，指的是坐标差等于可量度的长度或时间。这是一条自古以来的传统观念。多少年来，人们都是把时间看成是均匀流逝的时间，把空间看成是平直的空间，从来没有人怀疑，认为是理所当然的。也就是说，空间是欧几里得几何学的空间，可以用一组正交坐标系来表示。在同一参照系中有统一的时间、空间的测量标准，具有“刚性”的尺和“同步”的钟。

爱因斯坦认识到，洛伦兹变换的协变性对应于速度的相对性，因此对应于加速度的相对性以及加速度与引力场之间的等效性，就应该扩大为更普遍的非线性变换的协变性。1909—1912 年，他一直在思考这个问题，这时他正在苏黎世和布拉格大学讲授理论物理学。闵科夫斯基四维时空的数学表示形式，对爱因斯坦起到了很好的启发作用。他后来写道：“用了闵科夫斯基所给予狭义相对论的形式，相对论的这种推广就变得很容易；这位数学家首先清楚地认识到空间坐标和时间坐标形式上的等价性，并把它应用在建立这一理论方面。广义相对论所需要的数学工具已经在‘绝对微分学’（按：即张量分析）中完全具备”。[10]

在闵科夫斯基的四维时空几何学中的线元 ds 的平方表示为

\[{\rm{d}}{s^2} = {c^2}{\rm{d}}{t^2} - ({\rm{d}}{x^2} + {\rm{d}}{y^2} + {\rm{d}}{z^2})\]

其中（x，y，z，t）表示的是时空的四个坐标。在这一准欧几里得空间里，存在着一个不依赖于坐标的“刚性”度规，从而使坐标差直接与可量度的空间间隔、时间间隔联系起来；它对应于线性洛伦兹变换。对于爱因斯坦来说，要把线性洛伦兹变换推广到非线性变换，以适应于非惯性系或引力场中的物理现象，就应该把四维时空中两相邻事件的四维间隔（线元 ds）的平方表示成

\[{\rm{d}}{s^2} = \sum\limits_{\mu \nu } {{g_{\mu \nu }}{\rm{d}}{x_\mu }{\rm{d}}{x_\nu }} \]

式中 μ 和 ν 代表 1，2，3，4，g_μν 代表四维度规张量，是四个坐标的函数。这样一来，引力问题就归结为一个纯粹的数学问题了。要解决引力问题，建立普遍的新理论，研究 g_μν 的数学性质和物理意义就可以了。

1912 年初，爱因斯坦曾经分析过刚性转动圆盘，意识到在引力场中欧几里得几何并不严格有效。同时他还发现：洛伦兹变换不是普适的，需要寻求更普遍的变换关系；为了保证能量一动量守恒，引力场方程必须是非线性的；等效原理只对无限小区域有效。他意识到大学时学过的高斯曲面理论对建立引力场方程该会有用。

但是，爱因斯坦对这样的数学问题并不熟悉，于是，1912 年他找到老同学、苏黎世联邦工业大学数学教授格罗斯曼（M.Grossman，1878—1936），这立即引起了格罗斯曼的兴趣，爱因斯坦回忆道：“他查阅了文献并且很快发现，上面所提的数学问题早已由黎曼、里奇（Ricci）和勒维-契维塔（Levi-Civita）解决了。全部发展是同高斯的曲面理论有关的，在这一理论中第一次系统地使用了广义坐标系。”[11]

格罗斯曼帮助爱因斯坦引入黎曼张量运算，把平直空间的张量运算推广到弯曲的黎曼空间。1913 年，二人联名发表了《广义相对论和引力理论纲要》[12]一文，提出了引力的度规场理论。爱因斯坦负责物理学部分，格罗斯曼负责数学部分，文中第一次提出了引力场方程。他们把牛顿引力理论中的标量引力势 φ 的泊松方程

\[\Delta \varphi  = 4\pi \kappa \rho \]

推广为

\[\kappa {\Theta _{\mu \nu }} = {\Gamma _{\mu \nu }}\]

其中 κ 是引力常数，不变；质量密度 ρ 推广为物质系的能量张量 Θ_μν；Γ_μν 是由基本张量 g_μν 的导数构成的二秩抗变张量。在这里，用来描述引力场的不是标量 φ，而是度规张量 Γ_μν，即要用 10 个引力势函数来确定引力场。这是首次把引力和度规结合起来，使黎曼几何获得实在的物理意义。可是他们当时得到的引力场方程只对线性变换是协变的，还不具有广义相对性原理所要求的任意坐标变换下的协变性。这是由于爱因斯坦当时不熟悉张量运算，错误地认为，只要坚持守恒定律，就必须限制坐标系的选择，为了维护因果性原理，不得不放弃普遍协变的要求。

1915 年到 1917 年的 3 年是爱因斯坦科学成就的第二个高峰期。他在 1915 年最后建成了被公认为人类思想史中最伟大的成就之一的广义相对论，1916 年在辐射量子论方面作出了重大突破（详见第 11 章），1917 年又开创了现代科学的宇宙学。

1915 年的 10 月，爱因斯坦在经过了两年多的弯路之后，终于建成了广义相对论。这时他认识到放弃普遍协变要求的失误，回到普遍协变的要求，集中精力探索新的引力场方程，于 1915 年 11 月 4 日、11 日、18 日和 25 日一连向普鲁士科学院提交了 4 篇论文。在第一篇和第二篇论文《关于广义相对论》中他得到了满足守恒定律的普遍协变的引力场方程，但加了一个不必要的限制，那就是只允许幺模变换。第三篇论文《用广义相对论解释水星近日点运动》第一次用广义相对论计算出了水星的剩余进动，完满地解决了 60 多年来天文学一大难题，这给爱因斯坦以极大的鼓舞。他郑重声明：“在本文中我找到了这种最彻底和最完全的相对论的一个重要证明。”[13]。第四篇论文《引力的场方程》宣告广义相对论作为一种逻辑结构终于完成，在这里，他放弃了对变换群的不必要限制，建立了真正普遍协变的引力场方程。1916 年春天，爱因斯坦写了一篇总结性的论文《广义相对论的基础》；同年底，又写了一本普及性小册子《狭义与广义相对论浅说》。

爱因斯坦研究广义相对论，经历了一条比建立狭义相对论更漫长，也更艰难的探索道路。从 1907 年到 1916 年的九年时间，他的思想发展过程可划分为三个阶段：从 1907 年冬到 1912 年春的 4 年多时间里，他确立了广义相对论的两个基本原理；从 1912 年夏到 1915 年夏解决了广义相对论的数学表述；1915 年完成了普遍协变的引力场方程。

广义相对论的结构体系可以表示为如图 6 – 13。

迄今为止，广义相对论的应用主要是在宇观领域，即宇宙学和天体物理学方面。从广义相对论出发建立起来的引力理论是目前最好的一种引力理论。在现有的几种与广义相对论竞争的理论中，广义相对论占有明显的优势，不过它是不是惟一可能的正确理论，尚未有定论。所以人们非常关心对广义相对论的实验检验，并且期望通过各种实验检验，进一步丰富和发展这一理论。

[1] Einstein A.How I Created the Theory of Relativity.Phys.Today，1982，Aug：47

[2] 爱因斯坦文集，第一卷.商务印书馆，1977.320

[3] Einstein A.How I Created the Theory of Relativity.Phys.Today，1982，Aug：45

[4] 爱因斯坦文集，第一卷.商务印书馆，1977.320

[5] Newton I.Mathematical Principles of Natural Philosophy.University of California Press，1946.568

[6] 爱因斯坦全集，第二卷.湖南科技出版社，2002.407

[7] 爱因斯坦文集，第二卷.商务印书馆，1979.281

[8] 同上注，第284页。

[9] 爱因斯坦文集，第一卷.商务印书馆，1977.30

[10] 爱因斯坦文集，第二卷.商务印书馆，1979.278

[11] 爱因斯坦文集，第一卷.商务印书馆，1977.49

[12] 爱因斯坦全集，第四卷.湖南科技出版社，2002.258

[13] 爱因斯坦文集，第二卷.商务印书馆，1979.268

发布时间：2024/2/29 下午7:18:09  阅读次数：647