4.4 光的微粒说和波动说

什么是光？光的本性是什么？它由什么组成？每一位研究光学现象的物理学家都必然会涉及这些问题。从折射定律和色散现象的研究也可看出这一点。

笛卡儿主张波动说，认为光本质上是一种压力，在完全弹性的、充满一切空间的媒质（以太）中传递，传递的速度无限大。但他却又用小球的运动来解释光的反射和折射。牛顿倾向于微粒说，认为光可能是微粒流，这些微粒从光源飞出，在真空或均匀媒质中做惯性运动，但他在研究牛顿环时，却认识到了光的周期性，使他把微粒说和以太振动的思想结合起来，对干涉条纹作出了自己的解释。可见，不论是笛卡儿还是牛顿，都没有对光的本性作出肯定的判断。

4.4.1 早期的波动说

胡克明确主张光是一种振动，并根据云母片的薄膜干涉现象作出判断，认为光是类似水波的某种快速脉冲。在 1667 年出版的《显微术》一书中，他写道：

“在均匀媒质中，这种运动在各个方向都以同一速度传播，所以发光体的每个脉冲或振动都必然会形成一个球面。这个球面不断扩大，就如同把石块投进水中在水面一点周围的波或环，膨胀为越来越大的圆环一样（尽管要快得多）。由此可见，在均匀媒质中激起的这些球面的所有部分都与射线以直角相交。”

荷兰物理学家惠更斯发展了胡克的思想。他进一步提出光是发光体中微小粒子的振动在弥漫于宇宙空间的以太中的传播过程。光的传播方式与声音类似，而不是微粒说所设想的像子弹或箭那样的运动。1678 年他向巴黎的法国科学院报告了自己的论点（当时惠更斯正留居巴黎），并于 1690 年取名《光论》（Traite de la Lumiere）正式发表。他写道：

“假如注意到光线向各个方向以极高的速度传播，以及光线从不同的地点甚至是完全相反的地方发出时，其射线在传播中一条穿过另一条而互相毫无影响，就完全可以明白：当我们看到发光的物体时，决不会是由于这个物体发出的物质迁移所引起，就像穿过空气的子弹或箭那样。”[1]

罗默（Ole Rӧmer，1644—1710）在 1676 年根据木星卫蚀的推迟得到光速有限的结论（参看下节），使惠更斯大受启发。惠更斯根据罗默的数据和地球轨道直径计算出光速 c = 2×10⁸ 米/秒。这个结果虽然尚欠精确，却是第一次得到的光速值。于是惠更斯设想传播光的以太粒子非常之硬，有极好的弹性，光的传播就像振动沿着一排互相衔接的钢球传递一样，当第一个球受到碰撞，碰撞运动就会以极快的速度传到最后一个球。图 4 – 17 就是惠更斯自己画的一幅示意图。他认为，以太波的传播不是以太粒子本身的远距离移动，而是振动的传播。惠更斯接着写道：

“我们可以设想，以太物质具有弹性，以太粒子不论受到推斥是强还是弱都有相同的快速恢复的性能，所以光总以相同的速度传播。”[2]

图 4 – 18 是惠更斯描绘光波的示意图。这样，惠更斯就明确地论证了光是波动（他认为是以太纵波），进而以光速的有限性推断光和声波一样必以球面波传播。接着，惠更斯运用子波和波阵面的概念，引进了一个重要原理，这就是著名的惠更斯原理。他写道：

“关于波的辐射，还要作进一步考虑，即传递波的每一个物质粒子，不仅将运动传给从发光点开始所画直线上的下一个粒子，而且还要传给与之接触的并与其运动相对抗的其他一切粒子。结果是，在每个粒子的周围，兴起了以该粒子为中心的波。所以（如图 4 – 19），设 DCF 是从发光点 A 发出的并以该点为中心的波，则在球面 DCF 内的一个粒子 B，将产生自己独有的波（按：即子波）KCL，与这个波在 C 点触及波 DCF 的同时，从 A 点发出的主波也到达 DCF。显然，波 KCL 与波 DCF 的惟一接触点是在 AB 直线上，即 C 点。球面 DCF 内的其他点 bb、dd 等等也将类似地产生各自的波。每个这样的波与波 DCF 相比虽然都无限微弱，但所有这些波距 A 点最远的那部分表面却组成了波 DCF（按：即波阵面）。”

接着，惠更斯用他的原理说明了光的反射和折射。从他的理论可以推出与笛卡儿不同的折射公式：

\[\frac{{\sin i}}{{\sin r}} = \frac{{{v_i}}}{{{v_r}}}\]

1669 年丹麦的巴塞林纳斯（Erasmus Bartholinus，1625—1698）发现了双折射现象。当他用方解石（也叫冰洲石）观察物体时，注意到有双像显示。经过反复试验，他确定是这种晶体对光有两种折射：寻常折射和非寻常折射。

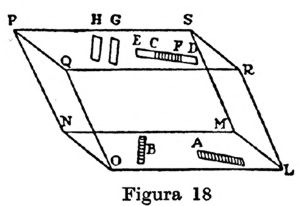
这是继干涉、衍射之后发现的又一光学新现象。对于这种新现象，是否能作出合理的解释，自然是微粒理论和波动理论面临的考验。惠更斯在得知巴塞林纳斯的发现后，立即重复进行了实验。他证实了这一现象，并且观察到在其他晶体，例如石英，也有类似效应，只是效果差些。进一步他还确定寻常折射仍然遵守折射定律，非寻常折射则不遵守折射定律。至于双折射现象的解释，惠更斯很巧妙地提出了椭球波的设想，认为方解石等晶体的颗粒可能具有特殊形状，以至光波通过时，在某一方向比在另一方向传播得更快一些，于是就出现了不同的折射。图 4 – 21 是惠更斯解释双折射的手稿：

惠更斯发展了波动理论。但是由于他把光看成像声波一类的纵波，因此不能解释偏振现象。他的波动理论也不能解释干涉和衍射现象，因为那时还没有建立周期性和位相等概念。早期的波动理论缺乏数学基础，还很不完善，而牛顿力学正节节胜利。以符合力学规律的粒子行为来描述光学现象，被认为是惟一合理的理论，因此，直到 18 世纪末，占统治地位的依然是微粒学说。

4.4.2 托马斯·杨的研究

托马斯·杨（ThomasYoung，1773—1829）是英国人，从小聪慧过人，博览群书，多才多艺，17 岁时就已精读过牛顿的力学和光学著作。他是医生，但对物理学也有很深造诣，在学医时，研究过眼睛的构造和其光学特性。就是在涉及眼睛接受不同颜色的光这一类问题时，对光的波动性有了进一步认识，导致他对牛顿做过的光学实验和有关学说进行深入的思考和审查。1801 年，托马斯·杨发展了惠更斯的波动理论，成功地解释了干涉现象。图 4 – 23 是他在论文中用于说明干涉现象的插图。他是这样阐述他的干涉原理的：

“当同一束光的两部分从不同的路径，精确地或者非常接近地沿同一方向进入人眼，则在光线的路程差是某一长度的整数倍处，光将最强，而在干涉区之间的中间带则最弱，这一长度对于不同颜色的光是不同的。”[3]

托马斯·杨明确指出，要使两部分光的作用叠加，必须是发自同一光源。这是他用实验成功地演示干涉现象的关键。许多人想尝试这类实验往往都因用的是两个不同的光源而失败。

在 1807 年的论文中托马斯·杨描述了他的双缝实验，他写道：

“使一束单色光照射一块屏，屏上面开有两个小洞或狭缝，可认为这两个洞或缝就是光的发散中心，光通过它们向各个方向绕射。在这种情况下，当新形成的两束光射到一个放置在它们前进方向上的屏上时，就会形成宽度近于相等的若干条暗带。……图形的中心则总是亮的。”

“比较各次实验，看来空气中极红端的波的宽度约为三万六千分之一英寸，而极紫端则为六万分之一英寸。”[4]

托马斯·杨所谓的“波的宽度”，就是波长。他得到的这些结果与近代的精确值近似相等。

双缝干涉实验为托马斯·杨的波动学说提供了很好的证据，这对长期与牛顿的名字连在一起的微粒说是严重的挑战。托马斯·杨说得好："尽管我仰慕牛顿的大名，但我并不因此非得认为他是百无一失的。我……遗憾地看到他也会弄错，而他的权威也许有时甚至阻碍了科学的进步。”[5]

果然，托马斯·杨由于提出干涉原理受到了一些权威学者的围攻，其中有一位以牛顿学术权威自居的布劳安（Henry Brougham）攻击得最为刻薄，说托马斯·杨的文章“没有任何价值"，“称不上是实验”，干涉原理是“荒唐”和“不合逻辑”的，等等。一二十年间，竟没有人理解托马斯·杨的工作。据说，托马斯·杨为回驳布劳安专门撰写的论文竟无处发表，只好印成小册子。小册子出版后，“只卖出了一本”。

1808 年，法国的马吕斯（Etienne Louis Malus，1775—1812）发现偏振现象，并认为找到了决定性的证据，证明光的波动理论与事实矛盾。然而，托马斯·杨面对困难并没有动摇自己的科学信念，他写信给马吕斯说：“您的实验证明了我采用的理论（即干涉理论）有不足之处，但是这些实验并没有证明它是虚伪的。”[6]经过几年的研究，托马斯·杨逐渐领悟到要用横波的概念来代替纵波，而这正是菲涅耳（Augustin Jean Fresnel，1788—1827）继续发展波动理论的出发点。

4.4.3 菲涅耳的贡献

菲涅耳是法国的一位工程师，对光学很感兴趣，曾发明一种用于灯塔的螺纹透镜，人称菲涅耳透镜。他精通数学，因此有条件在光学的数学理论方面作出特殊的贡献。1817 年 1 月 12 日，托马斯·杨写信给阿拉果，告诉他已找到了用波动理论解释偏振的线索，说：“用这个理论也可以解释沿半径方向以相等速度传播的横向振动，其粒子的运动是在相对于半径的某个恒定的方向。这就是偏振。”[7]1818年4月29日，托马斯·杨再次写信给阿拉果，又提到偏振问题，他把光比之于绳索的振动。阿拉果把这封信给菲涅耳看，菲涅耳立即看出这一比喻为互相垂直的两束偏振光之所以不能相干提供了真正的解释，而这一不相干性正可作为杨氏假说的极好佐证。

阿拉果和菲涅耳合作研究光学多年，互相垂直的两束偏振光的相干性是他们共同研究的课题，就这个课题已进行了多次实验，得到了重要成果。1819 年，他们联名发表了《关于偏振光线的相互作用》。但是当菲涅耳指出，只有横向振动才有可能把这个事实纳入波动理论时，阿拉果表示自己没有勇气发表这类观点，于是论文的第二部分乃以菲涅耳一人的名义发表。阿拉果在光学方面做出了许多贡献，但在关键问题上却令人遗憾地采取了暧味态度。菲涅耳的光学研究和法国科学院 1818 年的悬奖征文活动有一些联系。这次竞赛的题目是：

“①……利用精密的实验确定光线的衍射效应。

②根据实验用数学归纳法推导出光线通过物体附近时的运动情况。”[8]

竞赛的评奖委员会的本意是希望通过这次征文，鼓励用微粒理论解释衍射现象，以期取得微粒理论的决定性胜利。主持这项活动的著名科学家，例如：毕奥（J.B.Biot）、拉普拉斯和泊松（S.D.Poission）都是微粒说的积极拥护者。

然而，出乎意料的是，不知名的学者菲涅耳（当时只有 30 岁）以严密的数学推理，从横波观点出发，圆满地解释了光的偏振，并用半波带法定量地计算了圆孔、圆板等形状的障碍物所产生的衍射花纹，推出的结果与实验符合得很好，使评奖委员会大为惊讶。毕奥叹服菲涅耳的才能，写道：“菲涅耳从这个观点出发，严格地把所有衍射现象归于统一的观点，并用公式予以概括，从而永恒地确定了它们之间的相互关系。”[9]评奖委员泊松在审查菲涅耳的理论时，运用菲涅耳的方程推导圆盘衍射，得到了一个令人稀奇的结果：在盘后方一定距离的屏幕上影子的中心应出现亮点，如图 4 – 27。泊松认为这是荒谬的，在影子的中心怎么可能出现亮点呢？于是就声称这个理论已被驳倒。在这个关键时刻，阿拉果向菲涅耳伸出了友谊之手，他用实验对泊松提出的问题进行了检验。实验非常精彩地证实了菲涅耳理论的结论，影子中心果然出现了一个亮点。这一事实轰动了巴黎的法国科学院。

菲涅耳于是就荣获了这一届的科学奖，而后人却戏剧性地称这个亮点为泊松亮点。[10]

菲涅耳开创了光学研究的新阶段。他发展了惠更斯和托马斯·杨的波动理论，成为“物理光学的缔造者”。

[1] 转引自：Кубрявцев П С. История Физики，Т.1.Учпедгиз，1956.220 ~ 221

[2] 同上注。

[3] 转引自：Concise Dictionary of Scientific Biography.Charles Scribner’s Sons，1981.744

[4] 转引自：Magie W F.A Source Book in Physics.MeGraw-Hill，1935.310～311

[5] 梅森著，周煦良等译.自然科学史，上海译文出版社，1980.441

[6] Cajori F.A History of Physics.MacMillan，1933.154

[7] Cajori F.A History of Physics.MacMillan，1933.154

[8] Ъ.И.斯杰潘诺夫著，尚惠春译.光学三百年，科学普及出版社，1981.21

[9] Ъ.И.斯杰潘诺夫著，尚惠春译.光学三百年，科学普及出版社，1981.22

[10] 有人指出，这个故事可能夸大了亮点实验的作用。详情可阅：Worrall J.Fresnel,Poisson and the White Spot.In：Gooding D,et al,ed.The Uses of Experiment，Cambrigde Univ.Press,1989.137

发布时间：2024/2/14 下午3:06:18  阅读次数：4190