3.10 麦克斯韦电磁场理论的建立

3.10.1 法拉第的力线思想

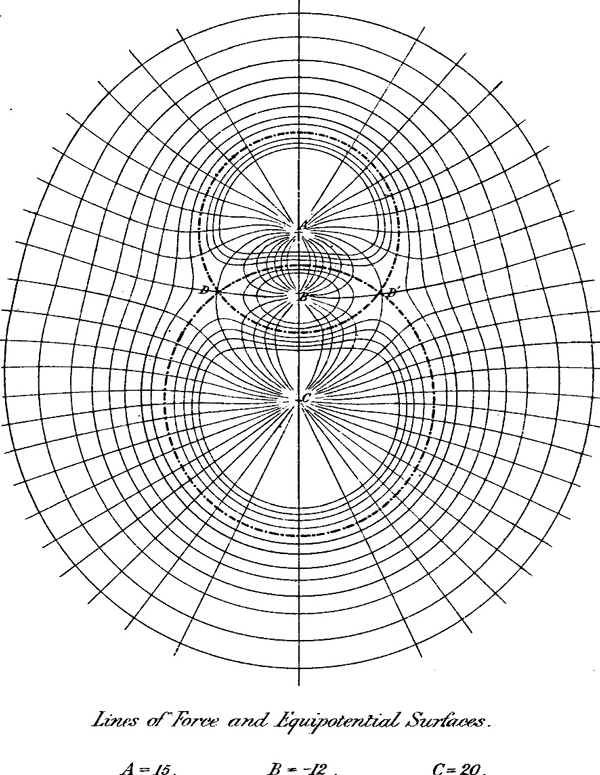
法拉第从广泛的实验研究中构想出描绘电磁作用的“力线”图像。他认为电荷和磁极周围的空间充满了力线，靠力线（包括电力线和磁力线）将电荷（或磁极）联系在一起。力线就像是从电荷（或磁极）发出、又落到电荷（或磁极）的一根根皮筋一样，具有在长度方向力图收缩，在侧向力图扩张的趋势。他以丰富的想象力阐述电磁作用的本质。

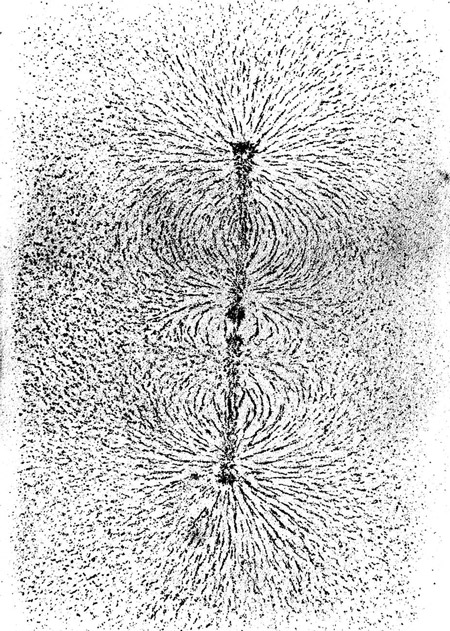
法拉第研究了电介质对电力作用的影响，认识到这一影响表明电力不可能是超距作用，而是通过电介质状态的变化；即使没有电介质，空间也会产生某种变化，布满了力线。后来，法拉第又进一步研究了磁介质，解释了顺磁性和反磁性。电磁感应现象则解释为磁铁周围存在某种“电应力状态"（electro-tonicstate），当导线在其附近运动时，受到应力作用而有电荷做定向运动；回路中产生电动势则是由于穿过回路的磁力线数目发生了变化。

法拉第的力线思想实际上就是场的观念，这是近距理论的核心内容。

3.10.2 W.汤姆孙的类比研究

在法拉第力线思想的激励下，W.汤姆孙对电磁作用的规律也进行过有益的研究。他从法国科学家傅里叶的热传导理论得到启示。傅里叶在 1824 年发表《热的分析理论》（Theorie analytique de la chaleur）一书，详细地研究了在介质中热流的传播问题，建立了热传导方程。这本书对 W.汤姆孙有很深的影响。

1842 年，W.汤姆孙发表了第一篇关于热和电的数学论文，题为：《论热在均匀固体中的均匀运动及其与电的数学理论的联系》，他论述了热在均匀固体中的传导和法拉第电应力在均匀介质中传递这两种现象之间的相似性。他指出电的等势面对应于热的等温面，而电荷对应于热源。利用傅里叶的热分析方法，他把法拉第的力线思想和拉普拉斯、泊松等人已经建立的完整的静电理论结合在一起，初步形成了电磁作用的统一理论。

1847 年，W.汤姆孙进一步研究了电磁现象与弹性现象的相似性，在题为《论电力、磁力和伽伐尼力的力学表征》一文中，以不可压缩流体的流线连续性为基础，论述了电磁现象和流体力学现象的共性。1851 年，他给出了磁场的定义，1856 年，根据磁致旋光效应提出磁具有旋转的特性，这样就为进一步借用流体力学中关于涡旋运动的理论，做好了准备。

W.汤姆孙运用类比方法，把法拉第的力线思想转变为定量的表述，为麦克斯韦的工作提供了十分有益的经验。

3.10.3 麦克斯韦建立电磁场理论的第一步

麦克斯韦在电磁理论方面的工作可以和牛顿在力学理论方面的工作相媲美。他和牛顿一样，是“站在巨人的肩上”，看得更深更远，作出了伟大的历史综合；他也和牛顿一样，其丰硕的成果是一步一步提炼出来的。

对于麦克斯韦来说，他是站在法拉第和 W.汤姆孙这两位巨人的肩上。他面对众说纷纭的电磁理论，以深邃的洞察力开创了物理学的新领域。然而，他也不是一蹴而就的。他在创建电磁场理论的奋斗中作了三次飞跃，前后历程达十余年。

麦克斯韦是英国人，1831 年生于爱丁堡，自幼聪慧过人，得到了精心培养。10 岁进爱丁堡书院（Edinburgh Academy）学习。15 岁就有几何学论文发表。1850 年入剑桥大学；这时 W.汤姆孙已是那里的研究员（fellow）。W.汤姆孙比麦克斯韦大 7 岁，他们先后荣获数学竟赛优胜者称号。W.汤姆孙对电磁理论的看法，麦克斯韦早有了解。在 W.汤姆孙的影响下，麦克斯韦特别注意斯托克斯的工作，这为以后的研究做了准备。从 1855 年起，麦克斯韦学习电学，认真阅读了法拉第的著作，特别是《电学实验研究》一书。他大学刚毕业，就着手把法拉第的力线思想用数学分析方法进行表述。

W.汤姆孙那两篇关于电磁现象与力、热现象相似性的论文对他很有影响。不但使他认识到类比方法的重要性，而且体验到法拉第的思想与传统的静电理论是协调的，有可能进一步建立统一的电磁理论。

1856 年，麦克斯韦发表了第一篇关于电磁理论的论文，题为：《论法拉第力线》。在这篇论文中，他发展了 W.汤姆孙的类比方法，用不可压缩的流体的流线类比于法拉第的力线，把流线的数学表达式用到静电理论中。流线不会中断，力线也不会中断，只能发源于电荷或磁极，或者形成闭合曲线。麦克斯韦通过类比，明确了两类不同的概念，一类相当于流体中的力，E 和 H 就是；另一类相当于流体的流量，D 和 B 属于这一类。麦克斯韦进一步讨论了这两类量的性质。流量遵从连续性方程，可以沿曲面积分，而力则应沿线段积分。

关于类比方法，麦克斯韦写道：

“为了采用某种物理理论而获得物理思想，我们应当了解物理相似性的存在。所谓物理相似性，我指的是在一门科学的定律和另一门科学的定律之间的局部类似。利用这种局部类似可以用其中之一说明其中之二。”麦克斯韦还特别注意到数学公式的类比。“精确科学的宗旨就是要把自然界的问题归结为通过数学计算来确定各个量。”[1]

这篇论文的第二部分专门讨论法拉第的“电应力状态”，对电磁感应作了理论解释。麦克斯韦指出，纽曼的矢势 A 正是表示“电应力状态”的一个函数，两者是一致的。不过，纽曼的矢势是建立在超距作用上的数学函数，缺乏实际含义，而法拉第的“电应力状态”则是根据大量实验发现并认真作出的精湛假设。麦克斯韦写道：

“也许有人会认为，多种现象的定量观测还未严密到足以形成数学理论的基础，但是法拉第并不满足于简单地叙述其实验的数学结果，也不希望靠计算来发现定律。当他掌握住一个定律时，他立即像对纯粹数学的定律一样，毫不含糊地讲出来；如果数学家把这个定律当作物理真理接受下来，从它推出其他可以用实验检验的定律，这位数学家只不过起了帮助物理学家整理自己思想的作用。当然，也要承认这是科学推理的必要步骤。”这里麦克斯韦提到的数学家实际上就是指他自己。

接着，麦克斯韦推出了 6 个定律：

“定律 Ⅰ  沿面积元边界电应力强度的总和等于穿过该面积的磁感应或等于穿过该面积的磁力线总数，”用现代的符号表示，就是

\[\oint {A \cdot dl = \Phi } \]

“定律 Ⅱ  任一点的磁（场）强度经一组叫做传导方程的线性方程与磁感应相联系，”即

\[B = \mu H\]

“定律 Ⅲ  沿任一面积边界的磁（场）强度等于穿过该面积的电流”，即

\[\oint {H \cdot dl = \sum I } \]

“定律 Ⅳ  电流的量与强度由一系列传导方程联系”，即

\[j = \sigma E\]

“定律 Ⅴ  闭合电流的总电磁势等于电流之量与沿同一方向围绕电路的电应力强度的乘积”，即：电磁能等于电路中电流与感应所生磁通的乘积，

\[W = \oint {j \cdot Adl} \]

“定律 Ⅵ  任一导体元中的电动势等于该导体元上电应力强度的瞬时变化率”，即

\[E =  - \frac{{{\rm{d}}A}}{{{\rm{d}}t}}\]

对于这 6 个定律，麦克斯韦写道：“在这 6 个定律中，我要表达的思想，我相信是（法拉第的）《电学实验研究》中所提示的思想模式的数学基础。”

3.10.4 麦克斯韦建立电磁场理论的第二步

隔了 5 年以后，麦克斯韦又回过来研究电磁理论，写了第二篇论文，题为《论物理力线》。其中分四个部分，分别载于 1861 年和 1862 年的《哲学杂志》上。他的“目的是研究介质中的应力和运动的某些状态的力学效果，并将它们与观察到的电磁现象加以比较，从而为了解力线的实质做准备。”[2]

两件事使麦克斯韦重新考虑他的研究方法：

一件是根据伯努利的流体力学，流线越密的地方压力越小，流速越快，而根据法拉第的力线思想，力线有纵向收缩、横向扩张的趋势，力线越密，应力越大，两者不宜类比。

另一件是电的运动和磁的运动也无法简单类比。从电解质现象中知道电的运动是平移运动，而从偏振光在透明晶体中旋转的现象看，磁的运动好像是介质中分子的旋转运动。

可见，电磁现象与流体力学现象有很大差别，电现象与磁现象不尽相同，靠几何上的类比无法洞察事物的本质。

于是麦克斯韦转向运用模型来建立假说。他借用兰金（W.J.M.Rankine）的“分子涡流”假设，提出自己的模型。他假设在磁场作用下的介质中，有规则地排列着许多分子涡旋，绕磁力线旋转，旋转角速度与磁场强度成正比，涡旋物质的密度正比于介质的磁导率。这个模型很容易解释电荷间或磁场间的相互作用，并清晰地体现了近距作用。

但是在进一步解释变化电场或变化磁场之间的关系时又遇到了困难。分子涡旋在旋转中相邻的边界沿相反的方向运动，这怎么可能呢？麦克斯韦从一种惰轮机构（如图 3 – 55）中想出了解决方案。他假设在涡旋之间有一层细微的带电粒子，将各涡旋隔开。带电粒子非常小，可在原地滚动（图 3 – 56），电流就相当于带电粒子的移动。图中六角形代表分子涡旋，小圆圈代表带电粒子。当电流流过 AB 时，AB 上面一排涡旋 gh 按逆时针方向旋转，通过中间粒子的啮合作用，逐一地传到各层涡旋，使它们都按逆时针方向旋转。AB 下面的涡旋则按顺时针方向旋转。当 AB 中电流发生变化，例如突然停止时，gh 中的涡旋旋转受到障碍，如果这时 kl 排的涡旋仍维持原来的运转速度，则 pq 中的粒子层就会从 p 向 q 运动，也就是在 pq 中产生同向感应电流。这样就很好地解释了电磁感应。

就在讨论“应用于静电的分子涡旋理论”这个问题时，麦克斯韦抓住了要害。他假设分子涡旋具有弹性。当分子涡旋之间的粒子受电力作用产生位移时，给涡旋以切向力，使涡旋发生形变，反过来涡旋又给粒子以弹性力。当激发粒子的力撒去后，涡旋恢复原来的形状，粒子也返回原位。这样，带电体之间的力就归结为弹性形变在介质中储存的势能，而磁力则归结为储存的转动能。位移的变化形成了电流。麦克斯韦称之为“位移电流”，他写道：

“只要导体上有电动势作用，就会产生电流，电流遇到电阻，就会将电能转化为热。这一过程的逆向却不可能将热重新储存为电能。

电动势作用于电介质，会使电介质的一部分产生一种极化状态，有如铁的颗粒在磁体的影响下极化一样分布，并且和磁极化一样，可以看成是每个粒子以对立状态产生（电）极。

在一个受到感应的电介质中，我们可以想象每个分子中的电都发生这样的位移，一端为正电，另一端为负电，而这些电仍然完全同分子联系在一起，不会从一个分子转移到另一个分子。

这种作用对于整个电介质是沿某一方面产生了总的位移。这一位移并不形成电流，因为它达到一定值时就保持不变了。但当电流开始时，和当位移时增时减因而形成不断变化时，就会根据位移的增加或减少，形成沿正方向或负方向的电流。”[3]

以 r 表示由于位移产生的电流值，h 表示位移值，麦克斯韦得出

\[r =  - \frac{{{\rm{d}}h}}{{{\rm{d}}t}},\;即\;{i_{位移}} = \frac{{{\rm{d}}D}}{{{\rm{d}}t}}\]

麦克斯韦提出的“位移电流”的假设在电磁场理论中具有非常重要的地位。这是一个重大的突破，在这以前，甚至在麦克斯韦去世时（1879 年）还没有人做出过可靠的实验，证明位移电流的存在。这说明了麦克斯韦具有何等的理论胆略！

还有一件事表明了麦克斯韦的理论威力，就是他预见到光是起源于电磁现象的一种横波。

既然电介质中的粒子位移可以看成是电流，就可以把电流与磁力线的相互作用推广到绝缘体，甚至是充填于真空的以太。在这些介质中任一点产生的电粒子的振动，就可以通过相互作用在介质中扩展开去。

设弹性介质密度为 ρ，切变模量为 m，这种介质可以传播速度为 v = \(\sqrt {\frac{m}{\rho }} \) 的横波。根据分子涡旋假设，麦克斯韦得到 v = \(\frac{E}{{\sqrt \mu  }}\)，其中 E 是取决于介质性质的一个特殊系数，μ 为磁导率，对于真空或空气，μ = 1。

柯尔劳胥（R.H.A.Kohlrausch，1809—1858）和 W.韦伯在 1857 年从莱顿瓶上测量电荷，根据静电单位和绝对单位的比值求出 E 值为：310740 千米/秒。麦克斯韦以之与斐索（Fizeau）1849 年用齿轮法测到的光速 c = 315 000 千米/秒比较，认为相符甚好。于是，麦克斯韦在论文中用斜体字写道：

“我们难以排除如下的推论：光是由引起电现象和磁现象的同一介质中的横波组成的。”[4]

3.10.5 麦克斯韦建立电磁场理论的第三步

1865 年麦克斯韦发表了关于电磁场理论的第三篇论文：《电磁场的动力学理论》（A dynamical theory of the electromagnetic field），全面地论述了电磁场理论。这时他已放弃分子涡旋的假设，然而他并没有放弃近距作用，而是把近距作用理论引向深入。

在这篇论文的引言中，他再次强调超距作用理论的困难，坚持假设电磁作用是由物体周围介质引起的。他明确地说：

“我提出的理论可以称为电磁场理论，因为它必须涉及电体和磁体附近的空间；它也可以称为动力理论，因为它假设在这一空间存在着运动的物质，观测到的电磁现象正是这一运动物质引起的。”

接着，麦克斯韦全面阐述了电磁场的含义，他指出：“电磁场是包含和围绕着处于电或磁状态的物体的那部分空间，它可能充有任何一种物质”，“介质可以接收和贮存两类能量，即由于各部分运动的‘实际能’（按：即动能）和介质因弹性从位移恢复时要作功的‘势能’。”[5]

然后，麦克斯韦讨论了电磁感应。他再次运用类比方法来说明电流的电磁动量（electromagnetic momentum），这个量代表了“电应力状态”，就是先前用过的矢势 A。在这篇论文中，麦克斯韦提出了电磁场的普遍方程组，共 20 个方程，包括 20 个变量。这 20 个变量是：电磁动量 F，G，H；磁力（即磁场强度）α，β，γ；电动热 P，Q，R；传导电流 p，q，r；电位移 f，g，h；全电流（包括位移的变化）pʹ，qʹ，rʹ；自由电荷电量 e；以及电势 ψ。

20 个方程是：

电位移方程：

\[\left. \begin{array}{l}p' = p + \frac{{{\rm{d}}f}}{{{\rm{d}}t}}\\q' = q + \frac{{{\rm{d}}g}}{{{\rm{d}}t}}\\r' = r + \frac{{{\rm{d}}h}}{{{\rm{d}}t}}\end{array} \right\}\]

磁场力方程：

\[\left. \begin{array}{l}\mu \alpha  = \frac{{{\rm{d}}H}}{{{\rm{d}}y}} - \frac{{{\rm{d}}G}}{{{\rm{d}}z}}\\\mu \beta  = \frac{{{\rm{d}}F}}{{{\rm{d}}z}} - \frac{{{\rm{d}}H}}{{{\rm{d}}x}}\\\mu \gamma  = \frac{{{\rm{d}}G}}{{{\rm{d}}x}} - \frac{{{\rm{d}}F}}{{{\rm{d}}y}}\end{array} \right\}\]

电流方程：

\[\left. \begin{array}{l}\frac{{{\rm{d}}\gamma }}{{{\rm{d}}y}} - \frac{{{\rm{d}}\beta }}{{{\rm{d}}z}} = 4\pi p'\\\frac{{{\rm{d}}\alpha }}{{{\rm{d}}z}} - \frac{{{\rm{d}}\gamma }}{{{\rm{d}}x}} = 4\pi q'\\\frac{{{\rm{d}}\beta }}{{{\rm{d}}x}} - \frac{{{\rm{d}}\alpha }}{{{\rm{d}}y}} = 4\pi r'\end{array} \right\}\]

电动势方程：

\[\left. \begin{array}{l}P = \mu \left( {\gamma \frac{{{\rm{d}}y}}{{{\rm{d}}t}} - \beta \frac{{{\rm{d}}z}}{{{\rm{d}}t}}} \right) - \frac{{{\rm{d}}F}}{{{\rm{d}}t}} - \frac{{{\rm{d}}\varphi }}{{{\rm{d}}x}}\\Q = \mu \left( {\alpha \frac{{{\rm{d}}z}}{{{\rm{d}}t}} - \gamma \frac{{{\rm{d}}x}}{{{\rm{d}}t}}} \right) - \frac{{{\rm{d}}G}}{{{\rm{d}}t}} - \frac{{{\rm{d}}\varphi }}{{{\rm{d}}y}}\\R = \mu \left( {\beta \frac{{{\rm{d}}x}}{{{\rm{d}}t}} - \alpha \frac{{{\rm{d}}y}}{{{\rm{d}}t}}} \right) - \frac{{{\rm{dH}}}}{{{\rm{d}}t}} - \frac{{{\rm{d}}\varphi }}{{{\rm{d}}z}}\end{array} \right\}\]

电弹性方程：

\[\left. \begin{array}{l}P = kf\\Q = kg\\R = kh\end{array} \right\}\]

电阻方程：

\[\left. \begin{array}{l}P =  - \rho p\\Q =  - \rho q\\R =  - \rho r\end{array} \right\}\]

自由电荷方程

\[e + \frac{{{\rm{d}}f}}{{{\rm{d}}x}} + \frac{{{\rm{d}}g}}{{{\rm{d}}y}} + \frac{{{\rm{d}}h}}{{{\rm{d}}z}} = 0\]

连续性方程

\[\frac{{{\rm{d}}e}}{{{\rm{d}}t}} + \frac{{{\rm{d}}p}}{{{\rm{d}}x}} + \frac{{{\rm{d}}q}}{{{\rm{d}}y}} + \frac{{{\rm{d}}r}}{{{\rm{d}}z}} = 0\]

实际相当于 8 个方程，其中 6 个是矢量方程，用现代符号表示，就是：

\[{\bf{C}} = {\bf{i}} + \frac{{\partial {\bf{D}}}}{{\partial t}}\tag{A}\label{A}\]

\[\mu {\bf{H}} = {\rm{curl}}{\bf{A}}\tag{B}\label{B}\]

\[{\rm{curl}}{\bf{H}} = 4\pi {\bf{C}}\tag{C}\label{C}\]

\[{\bf{E}} = \mu ({\bf{v}} \times {\bf{H}}) - \frac{{\partial {\bf{A}}}}{{\partial t}} - \nabla \varphi \tag{D}\label{D}\]

\[{\bf{E}} = k{\bf{D}}\tag{E}\label{E}\]

\[{\bf{E}} =  - \rho {\bf{i}}\tag{F}\label{F}\]

从电磁场理论的建立过程，我们又一次领会到壮伟的物理大厦是怎样一层一层地修筑起来的。

麦克斯韦生在电磁学已经打好基础的年代，他没有辜负时代的要求，及时地总结了已有的成就；他受到法拉第力线思想的鼓舞，又得到 W.汤姆孙类比研究的启发；他深刻地洞察了以纽曼和韦伯为代表的大陆派电动力学的困难和不协调因素，看穿那种力图把电磁现象归结于力学体系的超距作用理论的根本弱点，决心致力于近距作用理论。他从类比研究入手，开始只是借用适当的数学工具定量地表述法拉第的力线图像。后来，他感到有必要对力线的分布及其应力性质给予机理性的说明，乃转而运用模型理论。在这个过程中，他敏锐地抓住了位移电流和电磁波这两个关键概念。最后，他终于甩掉一切机械论点，径直把电磁场作为客体摆在电磁理论的核心地位，从而开创了物理学又一个新的起点。对麦克斯韦的功绩，爱因斯坦作了很高的评价，他在纪念麦克斯韦 100 周年的文集中写道：“自从牛顿奠定理论物理学的基础以来，物理学的公理基础的最伟大的变革，是由法拉第和麦克斯韦在电磁现象方面的工作所引起的”。“这样一次伟大的变革是同法拉第、麦克斯韦和赫兹的名字永远联在一起的。这次革命的最大部分出自麦克斯韦。”[6]麦克斯韦不愧为牛顿之后又一位划时代的杰出物理大师。[7]

爱因斯坦在这里提到赫兹是电磁波的发现者。实际上，赫兹在发展麦克斯韦的电磁场理论方面也有特殊贡献。应该补充的是，还有一位杰出的物理学家必须提到，这就是荷兰物理学家洛伦兹（H.A.Lorentz，1853—1928），是他把电磁场理论扩充到了与物质相互作用的领域。

[1] Scientific Papers of J.C.Maxwell，Vol.1.Cambridge，1890.156

[2] Scientific Papers of J.C.Maxwell，Vol.1.Cambridge，1890.491

[3] Scientific Papers of J.C.Maxwell，Vol.1.Cambridge，1890.491

[4] ScientificPapersofJ.C.Maxwell，Vol.1.Cambridge，1890.500

[5] Scientific Papers of J.C.Maxwell，Vol.1.Cambridge，1890.527

[6] 许良英等编译．爱因斯坦文集，第一卷，商务印书馆，1977.292

[7] 麦克斯韦不仅是伟大的理论家，也是卓有成效的实验家，他在晚年亲自筹备和主持了具有世界影响的剑桥大学卡文迪什实验室。参看本书 14.2.3 节。

发布时间：2024/2/5 下午5:21:05  阅读次数：552