3.6 安培奠定电动力学基础

在电磁学规律的定量表述方面，安培做出了特殊贡献。为了定量研究电流之间的相互作用，他从 1820 年开始，做了一系列实验和理论研究，其中尤以四个精巧的零值实验最为突出。所谓零值实验，是指两个电流同时作用于第三个电流而彼此平衡，从而判断电流相互作用的特性。他在这些实验的基础上进行数学推导，得到普遍的电动力公式，为电动力学奠定了基础。

第一个实验证明强度相等、方向相反的两个靠得很近的电流对另一电流产生的吸力和斥力在绝对值上是相等的。安培用一无定向秤检验对折的通电导线有无磁力作用。所谓无定向秤，实际上是悬吊在水银槽下两个方向相反的通电线圈（如图 3 – 32）。如果这两个线圈受力不均衡，就会发生偏转。实验结果是：当对折导线通电时，无定向秤丝毫不动。既然吸力和斥力在绝对值上相等，就可以用统一的公式来表示两种力。于是，安培就进一步设想两个电流元 ids 和 iʹdsʹ 的相互作用力可以表示成 ρ \(\frac{{ii'{\rm{d}}s{\rm{d}}s'}}{{{r^n}}}\)，这里 r 表示两个电流元的距离，ρ 是决定于电流元与距离的夹角 θ，θʹ 和电流元所在平面的夹角 ω 的函数，n 为一待定常数。

第二个实验证明电动力的矢量性。安培仍用无定向秤，将对折导线中的一根绕成螺旋状（如图 3 – 33），结果也是作用相互抵消，说明弯曲的电流和直线的电流是等效的，因此可以把弯曲电流看成是许多小段电流（即电流元）组成，它的作用就是各小段电流的矢量和。

第三个实验研究电动力的方向。安培把圆弧形导体架在水银槽上，经水银槽通电（如图 3 – 34）。改变通电回路或用各种通电线圈对它作用，圆弧导体都不动，说明电动力一定垂直于载流导体。

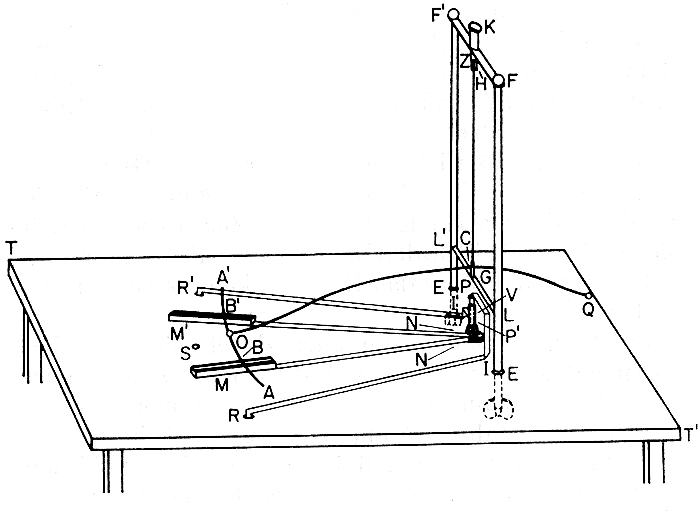
第四个实验检验电动力与电流及距离的关系。安培用三个相似的线圈（如图 3 – 35），其半径之比分别等于其距离之比。通电后，中间的线圈丝毫不动，说明第一个线圈和第三个线圈对第二个线圈的作用相互抵消。由此得出结论：载流导线的长度与作用距离增加相同倍数时，作用不变。据此，安培证明，电流元相互作用力的公式中的 n = 2，而 ρ = sinθ·sinθʹ·cosω + kcosθ·cosθʹ，其中 k 为一常数。

1827 年，安培通过数学推导，确定 k = − \(\frac{1}{2}\)。

于是，安培就在实验的基础上，推出了普遍的电动力公式，即：两电流元之间的作用力为

\[f = \frac{{ii'{\rm{d}}s{\rm{d}}s'}}{{{r^2}}}(\sin \theta  \cdot \sin \theta ' \cdot \cos \omega  - \frac{1}{2}\cos \theta  \cdot \cos \theta ')\]

这个公式为电动力学提供了基础。值得注意的是，安培的电动力公式从形式上看，与牛顿的万有引力定律非常相似。安培正是遵循牛顿的路线，仿照力学的理论体系，创建了电动力学。他认定电流元之间的相互作用力是电磁现象的核心，电流元相当于力学中的质点，它们之间存在电动力，而电动力是一种超距作用，就像牛顿的万有引力一样。

发布时间：2024/2/5 下午5:12:43  阅读次数：1900