2.2 热现象的早期研究

热学这门科学起源于人类对冷热现象的探索。从遥远的古代开始，人类就跟火打交道，学会利用火改造自然，为自己服务，从而获得了一种征服自然的有力武器。通过观察和实践，人们积累了大量有关烧、烤、物 体受热以及由此引起物性变化的知识，其中包括：热胀冷缩、蒸发凝结、冶炼烧焙等现象和运用这些现象的经验。大约到 17、18 世纪，测温学有了发展，进而产生了量热学，人们做了许多定量实验，热学才发展成为精确的科学。但是由于热学现象比较复杂，热学概念比较抽象，易于混淆，因此热学的发展远比力学晚。

2.2.1 温度计的发明和改进

冷热的观念从古就已有之，早在我国战国时期，我们的先人就已经根据水的结冰来推知气温下降的程度。汉代初年有一种“冰温度计”，按文献记载，“睹瓶中之冰而知天下之寒暑”，意思是说，观察瓶里冰的融化或增厚，就可知气温的变化。

古人也知道利用光的颜色判断温度的高低，“炉火纯青”就是形容炉温达到最高点时火焰从红色转成青色的意思。

最早有意识地依靠热胀冷缩来显示温度高低的是 16 世纪的几位科学家，其中有著名物理学家伽利略。伽利略发明温度计，时间大约是 1593 年。据他的学生描述，有一天，伽利略取一个鸡蛋大小的玻璃泡，玻璃泡接到像麦秸一般粗的玻璃管（图 2 – 1），管长约半米。用手掌将玻璃泡握住，使之受热，然后倒转插入水中，等玻璃泡冷却后，水升高约二三十厘米。伽利略用水柱的高度表示冷热程度，测量了不同地点、不同时候、不同季节的相对温度。

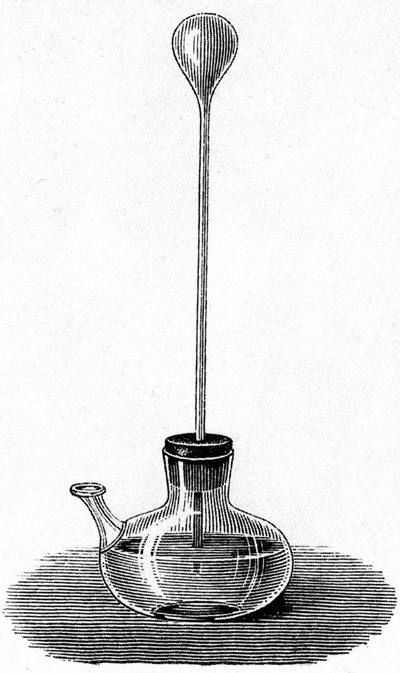
伽利略曾经学过医学，显然他是想利用这个温度计来测量人的体温。但他的温度计有一个重大缺点，就是大气压会对水柱高度产生影响，而且温度计插在水盆里用起来很不方便。

法国化学家雷伊（J．Rey）将伽利略的温度计做了一点改进，他把玻璃泡调头放在下方，从上面灌进一定量的水，于是温度计可以携带了。但水会蒸发，温度仍然不很可靠。不久，在意大利出现了把酒精或水银密封在玻璃泡中做成的温度计。为了表示温度的高低，在玻璃管上标有刻度，管子太长，就做成螺旋状。图 2 – 2 是当时发明的一种弯管温度计。可惜，刻度没有统一标准，不适于推广使用。

通过实践，科学家们逐渐认识到，为了有效地测量温度，必需选取某些温度作为标准点。惠更斯推荐水的冰点和沸点作为标准，玻意耳（R．Boyle，1627—1691）认为冰点会随纬度改变，建议用大茴香油的凝固点作为标准。牛顿则选用融雪温度和人体温度作为温标，并将这中间分成十二等份。1703 年，丹麦学者罗默（Ole Rӧmer）则选用冰、水和食盐的混合温度作为零点，因为这是当年所能达到的最低温度。

德国人华伦海特（G．D．Fahrenheit）从罗默的工作得到启发，也研究了温度标准。1714 年，他用水银代替酒精作为测温物质，于是就有可能利用水的沸点。他做了许多实验研究水的沸腾，认识到水的沸点在大气压一定的条件下是固定的，不同的大气压下，沸点会有所改变。他把结冰的盐水混合物的温度定为 0°，以健康人的体温为 96°，中间的 32° 正好是冰点，后来又确定水的沸点为 212°，这就叫华氏温标，以 ℉ 表示。

华伦海特的工作推动了精确温度计的发展，在欧洲大陆，他的温度计使用很普遍。

瑞典天文学家摄尔修斯（A．Celsius）1742 年创制的温度计是在水的冰点和沸点间分 100 等份。不过，他为了避免冰点以下出现负温度，定冰点为 100°，沸点为 0°，和现行的摄氏温标（以 ℃ 表示）正好相反。我们现在的摄氏温标是 1743 年法国人克利斯廷（Christin）首先采用的。从伽利略到摄尔修斯，大约经过了 180 年，在这些漫长的岁月里，温度计几经沧桑，逐渐完善。有了温度计，没有温度标准和分度规则也是不行的；而温度标准则有待于物态变化的研究。所以，温度计的发展历经这么长的时间。而一旦建立了完善的测温术，热学的实验研究也就蓬勃地展开了。

2.2.2 蒸汽机的发明和应用

蒸汽机的历史可以追溯到古希腊时代。公元 50 年，希罗（Heron）发明过一种演示用的蒸汽轮球，如图 2 – 3。当加热后蒸汽从喷嘴喷出时，轮球就会沿相反方向旋转。可是当时这一创造成果并没有得到实际应用，发明者自己也没有这种打算。一千多年过去了，当工矿业有了发展，才有人企图制造从矿井里排水的蒸汽泵。1630 年就有人曾因发明以蒸汽为动力的提水机械而获专利，不过所有活动都只限于设计或试制，没有实用价值。德国的巴本（D．Papin），英国的萨弗里（T．Savery）和纽可门（T．Newcomen）可以说实际上是蒸汽机的发明者。

萨弗里是英国工程师，他在 1689—1712 年间，先后创制了几种蒸汽机。其中有一种直接用于提水的机器，如图 2 – 4。工作原理是：蒸汽从锅炉通过打开的阀门进入汽包，再把水从那里通过活动阀（这时另一活动阀关闭）压到储水池，当汽包中的水所剩无几时，关上阀门，从水箱向汽包放水冷却，于是汽包内形成负压。在大气压的作用下，水从吸筒进入汽包。如此周而复始，达到连续抽水的目的。这种蒸汽机提水的高度据说只有 7 米，每小时可提水十几吨。但它需有人每隔十几秒关一次阀门。如果忘记及时启闭阀门，就有可能引起锅炉爆炸。再加上矿井很深，往往需用几台蒸汽机分几个台阶提水，既不经济，也欠安全，厂矿主不大愿意采用。

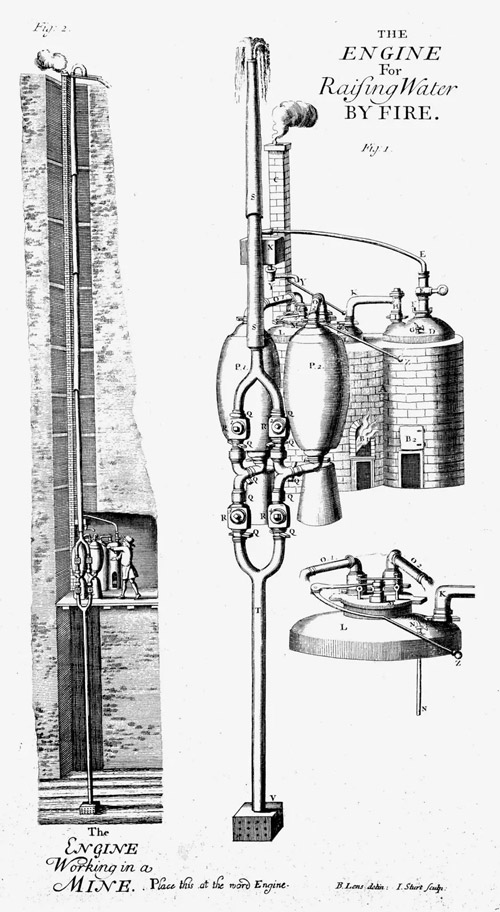
纽可门的蒸汽机是进一步改进的产物。纽可门是一位铁匠。他在活塞（图 2 – 5）上加了一庞大的摇臂，摇臂的一侧挂有平衡重物，重物下面连着抽水唧筒杆。重物由于自身重量下降时，拉活塞升起，蒸汽从锅炉经过打开了的阀门进入汽包，这时通向汽包的水门打开，冷水从水箱进入汽包，使蒸汽冷凝，汽包内形成负压。在大气压的作用下，活塞向下移动，将抽水唧筒杆提起。

纽可门蒸汽机的优点是把动力部分的抽水唧筒分开，气压较低，比较安全。后来又有人用飞轮把阀门启闭的工序自动化，于是就有不少矿山乐于采用。

然而，纽可门蒸汽机的效率非常之低，直到 1769 年瓦特（James Watt，1736—1819）作出进一步改进（图 2 – 6），蒸汽机才得到广泛应用。

瓦特是苏格兰发明家，1736 年 1 月 19 日生于格林诺克的工人家庭里，由于家庭影响从小就熟悉机械制造的基本知识，18 岁到伦敦一家钟表店当学徒工，学会了使用工具和制造器械的手艺。他利用业余时间刻苦学习，努力实践，掌握了制造罗盘、象限仪、经纬仪等复杂仪器的技术。后来瓦特进到格拉斯哥大学，负责教学仪器的修理，在修理工作中进一步熟悉了这种蒸汽机的结构，搞清了它的原理，并找到了效率低的原因。原来，纽可门蒸汽机的汽缸每次推动活塞后都要喷进冷水，使蒸汽凝结，所以汽缸要反复加热，白白消耗掉许多热能。1769 年瓦特发明冷凝器，解决了制造精密汽缸和活塞的工艺，创造了单动作蒸汽机。经过不断试验，他又发明了双动作蒸汽机，从汽缸两边推动活塞动作。他利用曲柄机构，使往复的直线运动转变为旋转运动。他还设计了离心式节速器控制蒸汽机的转速。经过他一系列革新，蒸汽机逐步完善，效率也大有提高。工业界广泛采用蒸汽机，促进了产业革命的到来。

2.2.3 热质说的兴起

在 18 世纪中叶之前，人们往往把热和温度混为一谈，两个概念混淆在一起。当时人们常说：“某某物体损失了多少度热”，其实这里热指的是温度。著名化学家布尔哈夫（Herman Boerhaave，1668—1738）也没有分清这两个概念，1724 年他写道："相同体积的不同物体应含相同的热量，因为不管温度计插在哪里，都指示同样的热度。”显然，他在温度和热量间没有找到正确的关系，他还没有热容量的概念。

不过，布尔哈夫对热学还是有贡献的，他根据物体混合时热量交换的现象，首先提出了热量守恒的思想。他写道：“物体在混合时，热不能创造，也不能消灭。”

例如，将 40 ℃ 的水和同体积的 80 ℃ 的水相混合，混合后的水温应为 60 ℃。实验证明，情况正是这样。但是如果将 40 ℃ 的水和同体积的 80 ℃ 的酒精相混合，就不是 60 ℃，而是低于 60 ℃。布尔哈夫没有办法解释这一事实。

1740 年左右，俄国学者里赫曼（Γ．Β．PихманHxMaH，1711—1753）用“混合法”研究热的传递。他根据经验建立了如下关系：

\[混合后的“热”（即温度） = \frac{{am + bn +  \cdots }}{{a + b +  \cdots }}\]

其中 m，n … 是质量为 a，b … 的物体的热（温度）。显然他还没有建立比热的概念，但上面的公式精确地表示了热量守恒的规律。

热量守恒定律是量热学中最核心的内容，英国化学家布莱克（J．Black，1728—1799）在这个定律的发现和运用上发挥了特殊的作用。

布莱克研究了不同温度的水和水银混合后的温度，认识到混合后的温度既不与这两种物质的体积成正比，也不与重量成正比，“以等量的热质加热水银比加热等量的水更有效，要使等量（指重量）的水银增加同样的‘热度’（指温度），更少的热质即已足够……可见，水银比水对热质具有更小的容量。”

就这样，布莱克发现了热容量。后来，他的学生罗巴松在 1803 年将他的概念加以发展，提出不同物质具有不同比热。

潜热也是布莱克发现的。他受到两个实验的启示。

一个是卡伦（W．Cullen，1710—1790）的乙醚实验。乙醚的挥发性很强，蒸发时会出现骤冷现象。布莱克想，这显然是乙醚蒸气带走了大量“热质”，来不及补充的缘故。

另一个实验是华伦海特观察到的。他描述过这样一个现象，一盆水如果不受任何摇晃，保持绝对静止，往往可以冷却到冰点以下而不致凝固。布莱克正确地解释：这是由于静水中热量散失缓慢造成的。

布莱克自己做了这样的实验，他把 0 ℃ 的冰块和相等重量的 80 ℃ 的水相混合，结果发现，平均水温不是 40 ℃，而是维持于 0 ℃，冰的温度毫无变化，只是全部化成了水，可见，冰在融化时吸收了大量的热。

布莱克由此判断：物态转变的过程，不论是固化还是液化，都会同时伴有“热质”的转移。

这种转移用温度计是观察不出来的，所以，布莱克称之为“潜热”。

布莱克之所以能对众多的热学现象作出正确的说明，一方面是由于他做了大量的热学实验，深入地研究了其中的规律性；另一方面是他通过认真的分析，区分出热量和温度是两个不同的概念。

但是由于时代的局限性，他的工作也促使另一个错误概念得到巩固，这就是所谓的热质。他陷入了热质说的泥坑。热质说的大意是：热是一种特殊的物质，这种物质（热质）在自然界中普遍存在，总量守恒，既看不见，也摸不着，没有固定的形状，总是伴随着各种物体。物体温度升高，所含热质增多；物体温度降低，热质就转移到别的物体。热质说能解释许多热学现象，特别是混合量热实验。因为“热量守恒”很容易使人联想到“物质守恒”，所以布莱克的工作加强了热质的地位。到了 18 世纪末，热质说竟成了热学的统治学说，大多数科学家都相信热质说。

热质说对热的本质作出了错误的解释，但是以布莱克为代表的科学家仍然对热学的发展做出了重要贡献。18 世纪末著名化学家拉瓦锡（A．Lavoisier，1743—1794）继续从事量热学研究，他和法国物理学家拉普拉斯合作，做了许多热学实验，他们发明了精确测量热量的冰卡计。

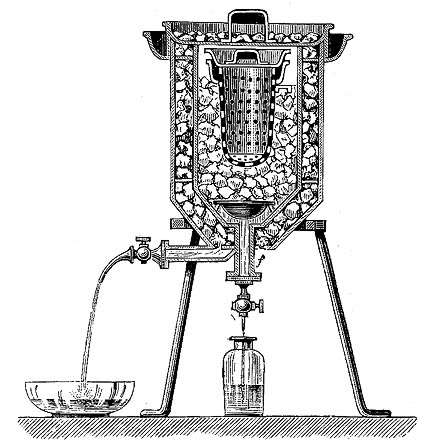
冰卡计的原理很简单，但结果甚为精确，装置如图 2 – 9 所示。器壁有三层，物质 B 放在内腔 A 室，它的温度比较高，使 C 室的冰逐渐融化成水，水经活栓 T 流到量杯。外层 D 也充满冰，起着维持在冰点的作用。由 D 流出的水排到另一容器，不必计量。称出量杯中的水重，即可求出 C 室冰所吸收的热量。这个装置设计得十分巧妙，可以用来测量各种物质的比热，包括固体、液体和气体，它的妙处就在于，除了水流经活栓和在冰上残留的水粒造成误差以外，避免了各种外界干扰的影响。

2.2.4 传热学的成就

以热质说作为主导思想的热学分支，除了量热学之外，还有研究传热现象的传热学。传热学从 18 世纪初就建立了定量的规律，这就是牛顿在 1701 年发表的冷却定律；热的损失率正比于温度差。用数学式可表述为

\[\frac{{{\rm{d}}Q}}{{{\rm{d}}t}} =  - \lambda (T - {T_0})\]

式中 dQ 表示物体单位表面上在时间 dt 内所损失的热量，T 为物体的温度，T₀ 为周围介质的温度，λ 为一系数。杜隆（P．L．Dulong，1785—1838）和珀替（A．Petit，1791—1820）在 1819 年发表论文指出，牛顿的冷却定律只在温度差较小时才适用。

兰伯（J．H．Lambert，1728—1777）也是研究热传导的先驱者，他曾经做过许多热传导实验，这在他死后的 1779 年出版的一本书《测高温学》中有记载，其中包括热沿杆的传播。他讨论了稳定状态下杆的温度分布，他还指出热射线与光线类似，是沿直线传播的，其强度与距离的平方成反比。

1804 年，毕奥（J．B．Biot，1774—1862）根据热量守恒的思想建立了初步的热传导理论，接着傅里叶（Joseph Fourier，1768—1830）在 1807 年向巴黎科学院呈交了一篇关于热传导的论文。由于拉格朗日等人认为推理缺乏严密性，论文没有通过。1811 年，傅里叶呈交了修改过的论文，但仍未能在法国科学院的《报告》中发表。傅里叶继续对这一课题进行研究，终于在 1822 年写成《热的分析理论》一书，这本书总结了他在这一领域内多年研究的成果。

在吸收或者释放热的物体内部，温度分布一般是不均匀的，在任何点上都随时间而变化，所以温度 T 是空间（x，y，z）和时间 t 的函数。傅里叶证明 T 必须满足偏微分方程

\[\frac{{{\partial ^2}T}}{{\partial {x^2}}} + \frac{{{\partial ^2}T}}{{\partial {y^2}}} + \frac{{{\partial ^2}T}}{{\partial {z^2}}} = {K^2}\frac{{\partial T}}{{\partial t}}\]

这就是三维空间的热传导方程。其中 K² 是一个依赖于物体质料的常数。傅里叶根据这一方程解决了在稳定状态下杆、球、环和立方体的温度分布问题。

傅里叶还研究了物体内部的热传导问题，总结出热传导公式

\[\frac{{{\rm{d}}Q}}{{{\rm{d}}t}} = KS\frac{{{\rm{d}}T}}{{{\rm{d}}x}}\]

式中 K 是依赖于导热物质性质的导热系数，dQ/dt 为通过厚为 dx 层的物体，每单位时间传导的热流量，它正比于层界面上的温度梯度 dT/dx 和层的面积 S。

傅里叶的成果得到了泊松（Simeon D．Poisson，1781—1840）的肯定。泊松也是热学理论的先驱者，从 1815 年起致力于热传导问题，后来发表在他的《热的数学理论》（1835 年）一书中。

发布时间：2024/1/29 下午9:00:01  阅读次数：1615