分力与分量
在求解动力学问题时,为了能根据研究对象的运动特征,利用牛顿第二定律列出相应的运动方程,往往需要把研究对象所受的诸力按正交分解法进行分解。于是,引入了“力的分量”概念,下文简称分量。但有些参考书又常把“力的分量”称为“分力”。这样,自然就使不少同学把应有区别的“分量”与“分力”这两个概念混为一谈。下面就这两个概念的区别和联系作一些讨论。
设有一平面力F,作用在A点,则力F的正交分解如图1所示。
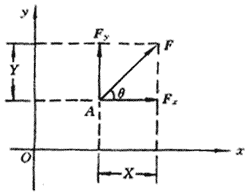
(1)图中Fx、Fy分别是力F的两个分力。既然都是力,那么它们都具备力的“三要素”,都是矢量。显然,它们的作用点都是原力F的作用点A。图中X、Y分别是力F在x轴和y轴上的“投影”,称为力F在x轴和y轴上的分量。因为投影是个代数量,有正、负之分,故作为力F的分量X、Y也是代数量而不是矢量。
(2)从图可知,力F的两个分力Fx、Fy的大小与力F在相应坐标轴上的分量绝对值相等,即|Fx|=|X|,|Fy|=|Y|。
(3)从图可知,力F的两个分量分别可按下式计算:
X=|F|cosθ
Y=|F|sinθ
分量X、Y的正、负号完全由θ值的大小决定。当
θ=0时,X=|F|,y=0;
当θ=π/2 时,X=0,y=|F|;
当0<θ<π/2 时,X>0,Y>0;
当π/2 <θ<π时,X<0,Y>0。
可见,力F的分力Fx、Fy的方向跟其在z轴和y轴上的两个分量的正、负号紧密联系着。分量为正,则表示分力方向与相应坐标轴的正方向一致;分量为负,则表示分力方向与相应坐标轴的负方向一致。
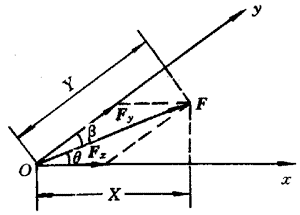
(4)如力F沿两个不正交的坐标轴分解,分力的大小就与分量的绝对值不等。如图2所示,力F在x轴和y轴上的分力是Fx和Fy,而相应的分量是X和Y。显然,|Fx|≠|F|cosθ=X,|Fy|≠|F|cosβ=Y 。
发布时间:2009/3/20 上午7:17:16 阅读次数:11614
