第 2 章 第 2 节 法拉第电磁感应定律

我们知道，穿过闭合回路的磁通量发生变化时，会有感应电流产生。这是为什么呢？学习了本节内容之后，你便知道其中的原因了。

1．感应电动势

在电磁感应现象里，若闭合回路中有感应电流，则必然存在电动势。这种在电磁感应现象中产生的电动势被称为感应电动势（induction electromotive force）。产生感应电动势的那部分导体相当于电源。

感应电动势是由闭合回路中磁通量的变化产生的。它的大小与磁通量的变化有什么关系呢？让我们通过实验进行探究。

实验与探究

感应电动势与磁通量变化的关系

如图 2–8 所示，用螺线管与电流计组成闭合回路。将条形磁铁以不同速度插入或拔出螺线管，观察电流计指针偏转的角度情况。

由实验探究可知，条形磁铁插入或拔出螺线管的速度越大，螺线管中磁通量的变化越快，电流计显示的电流越大，表明电路中的感应电动势就越大。研究表明，感应电动势的大小与电路中磁通量变化的快慢有关。

进一步的研究表明，当磁通量变化而电路断开时，虽然没有感应电流，但电路中仍有感应电动势，感应电动势的产生与电路是否闭合无关。因此，感应电动势比感应电流更能反映电磁感应现象的本质。

迷你实验室

观察发光二极管亮度的变化

如图 2–9 所示，用一个多匝线圈与发光二极管组成闭合回路。将强磁铁插入线圈中，观察发光二极管的亮度与什么因素有关。

2．电磁感应定律

磁通量变化快慢可用单位时间内磁通量的变化量来表示。单位时间内磁通量的变化量通常称为磁通量的变化率。也就是说，感应电动势的大小与磁通量的变化率有关。进一步的实验表明：电路中感应电动势的大小与穿过这一电路的磁通量的变化率成正比。这就是法拉第电磁感应定律（Faraday law of electromagnetic induction）。

设在 t₁ 时刻穿过闭合回路的磁通量为 Φ₁，t₂ 时刻穿过闭合回路的磁通量为 Φ₂，则在 Δt = t₂ − t₁ 这段时间内，穿过闭合回路的磁通量的变化量 ΔΦ = Φ₂ − Φ₁，磁通量的变化率为 \(\frac{{\Delta \Phi }}{{\Delta t}}\)。设感应电动势为 E，则法拉第电磁感应定律可表示为

E = k \(\frac{{\Delta \Phi }}{{\Delta t}}\)

式中，k 为比例常数。在国际单位制中，感应电动势 E 的单位是伏特（V），磁通量 Φ 的单位是韦伯（Wb），时间 t 的单位是秒（s）。此时，k = 1，上式可简化为

E = \(\frac{{\Delta \Phi }}{{\Delta t}}\)

在实际应用中，为了获得较大的感应电动势，常常采用多匝线圈。n 匝线圈可视为由 n 个单匝线圈串联组成，如果穿过每个单匝线圈的磁通量的变化率都是 \(\frac{{\Delta \Phi }}{{\Delta t}}\)，则 n 匝线圈的感应电动势为

E = n \(\frac{{\Delta \Phi }}{{\Delta t}}\)

感应电动势是标量，但有方向。其方向规定为从电源的负极经过电源内部指向电源的正极，与电源内部电流方向一致。因此，运用楞次定律判断出感应电流的方向，也就判断出了感应电动势的方向。

当磁通量的变化量仅由导线切割磁感线引起时，感应电动势的公式还可写成另一种形式。如图 2-10 所示，在磁感应强度为 B 的匀强磁场中，矩形线框 abcd 平面与磁感线垂直。设线框中可移动部分 ab 的长度为 l，以速率 v 匀速向右做垂直切割磁感线的运动，在时间 Δt 内移动了 Δx，线框的面积变化量 ΔS = lΔx = lvΔt，穿过闭合回路的磁通量的变化量 ΔΦ = BΔS = BlvΔt。代入公式 E = \(\frac{{\Delta \Phi }}{{\Delta t}}\) 中，可得到感应电动势

E = Blv

图 2–10 导线切割磁感线示意图

式中，B 的单位是特斯拉（T），l 的单位是米（m），v 的单位是米每秒（m/s）。

如果长为 l 的导体垂直于纸面放置，以速度 v 沿与磁场方向成 θ 角的方向运动。在这种情况下，可将速度 v 分解为垂直和平行于磁场方向的两个分量 v₁ = vsinθ 和 v₂ = vcosθ（图 2–11）。导体在 v₂ 方向不切割磁感线，不会产生感应电动势，在 v₁ 方向切割磁感线，产生的感应电动势即为导体中的感应电动势

E = Blvsinθ

图 2–11 磁场中导线运动速度分解示意图

拓展一步

感生电动势与动生电动势

感应电动势是由回路中磁通量的变化引起的，根据磁通量变化的原因不同，可分为感生电动势和动生电动势。由磁场变化引起磁通量变化而产生的感应电动势称为感生电动势。变化的磁场在其周围空间会激发出感应电场（称为涡旋电场），这种电场迫使导体内的电荷做定向移动而产生感生电动势（图 2–12）。导体切割磁感线产生的电动势称为动生电动势。导体切割磁感线时，导体中的自由电子由于和导体一起运动，因而受到洛伦兹力的作用，使导体两端产生电动势（图 2–13）。

图 2–12 产生感生电动势示意图

图 2–13 产生动生电动势示意图

例题

在一个磁感应强度大小随时间变化的磁场中，垂直于磁场方向放一个面积为 0.10 m² 的线圈。在 0.20 s 内磁场各点的磁感应强度由 0 增大到 0.30 T，求线圈中的平均感应电动势。

分析

已知线圈与磁场垂直，线圈的面积和磁感应强度在一段时间的初、末时刻的大小，用法拉第电磁感应定律可求解。

解

开始时，穿过线圈的磁通量 Φ₁ = 0，经 0.20 s 后穿过线圈的磁通量增大到 Φ₂ = BS = 0.30 ×0.10 Wb = 3.0×10⁻² Wb

ΔΦ = Φ₂ − Φ₁ = 3.0×10⁻² Wb – 0 = 3.0×10⁻² Wb

在这段时间内，线圈中平均感应电动势的大小

E = \(\frac{{\Delta \Phi }}{{\Delta t}}\) = 3.0×10-20.20V = 0.15 V

讨论

若这个线圈一共有 20 匝，产生的电动势为多大？

策略提炼

运用法拉第电磁感应定律分析求解问题，若感应电动势由导体切割磁感线产生，选择 E = Blv 进行计算比较方便；若感应电动势由磁感应强度的变化产生，则应选择 E = n \(\frac{{\Delta \Phi }}{{\Delta t}}\) 进行计算，运用此式求出的一般是 Δt 时间内的平均感应电动势。当磁通量均匀变化或 Δt 趋于零时，E 为瞬时感应电动势。

这类问题常与电路、磁场知识综合，甚至涉及力学知识，这时需要综合相关知识进行分析求解。

迁移

如果感应电动势由导体切割磁感线产生，又应该如何分析求解呢？如图 2–14 所示，两条相距 50 cm 的光滑平行金属导轨位于同一水平面内，左端接一阻值为 0.5 Ω 的电阻，一根与导轨垂直的金属棒 ab 置于两导轨上。整个装置置于磁感应强度为 0.5 T 的匀强磁场中。线框平面、金属棒速度方向均与磁场方向垂直。假定导体 ab 以 4 m/s 的速度向右做匀速运动。不计金属棒及导轨的电阻，求：

（1）金属棒中感应电动势的大小及方向；

（2）金属棒受到的安培力的大小及方向。

参考解答：（1）由 b 指向 a

（2）水平向左

DIS实验室

探究感应电动势与磁通量变化率的关系

实验装置如图 2-15 所示。通过电源使线圈 1 中的电流发生变化，利用传感器即可得到线圈 1 产生的磁感应强度随时间变化的图像［图 2–16（a）］，以及线圈 2 中对应的感应电动势随时间变化的情况［图 2–16 （b）］。由此可得，在线圈横截面积一定的情况下，感应电动势与磁感应强度的变化率成正比，即感应电动势与穿过线圈的磁通量变化率成正比。

节练习

1．将长约 15 m 的铜芯双绞线两端接在灵敏电流计上，拉开形成一个长回路。面对面站立的两位同学像甩跳绳那样以每秒 4 ~ 5 圈的频率摇荡半个回路，如图所示。观察电流计指针的摆动情况并解释原因。换一个站位方向，再试一试。两位同学沿南北方向站立还是沿东西方向站立时实验现象更明显？这是为什么呢？

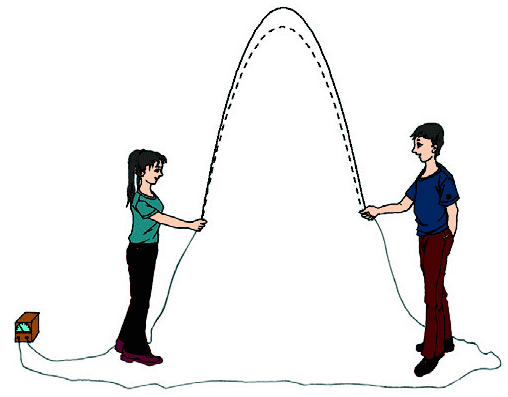
参考解答：电流计指针将发生偏转，说明有感应电流产生，因为导线在地磁场中切割了磁感线，回路中的磁通量发生改变。换一个站位方向，电流计指针的摆动情况会发生改变，因为导线切割磁感线的方向不同了。两位同学沿东西方向站立时，实验现象更明显，因为地球附近的地磁场，磁感线几乎与地面平行，由地理南极指向地理北极，这种情况下，导线切割磁感线更厉害，线圈中的磁通量的变化率更大。

2．有一种非接触式电源供应系统，这种系统基于电磁感应原理可无线传输电力。其工作原理可用两个左右相邻或上下相对的线圈来说明，如图所示。下列说法正确的是

A．若线圈 A 中输入电流，则线圈 B 中会产生感应电动势

B．只有线圈 A 中输入变化的电流，线圈 B 中才会产生感应电动势

C．线圈 A 中电流越大，线圈 B 中感应电动势也越大

D．线圈 A 中电流变化越快，线圈 B 中感应电动势越大

参考解答：BD

3．无线充电技术中使用的受电线圈示意图如图所示，线圈匝数为 n，面积为 S。若在 t₁ ~ t₂ 这段时间内，匀强磁场平行于线圈轴线向右穿过线圈，其磁感应强度大小由 B₁ 均匀增加到 B₂，则该段时间内线圈两端 a 和 b 之间的电势差

A．恒为 \(\frac{{nS({B_2} - {B_1})}}{{{t_2} - {t_1}}}\)

B．从 0 均匀变化到 \(\frac{{nS({B_2} - {B_1})}}{{{t_2} - {t_1}}}\)

C．恒为 − \(\frac{{nS({B_2} - {B_1})}}{{{t_2} - {t_1}}}\)

D．从 0 均匀变化到 − \(\frac{{nS({B_2} - {B_1})}}{{{t_2} - {t_1}}}\)

参考解答：C

4．航天飞机在环绕地球的轨道上飞行时，从中释放一颗卫星。若卫星与航天飞机保持相对静止，二者用导电缆绳相连，这种卫星称为绳系卫星。现有一颗绳系卫星在地球赤道上空自西向东运行，卫星位于航天飞机的正上方，它与航天飞机间的距离是 20.5 km（远小于航天飞机的轨道半径），它们所在处的地磁场的磁感应强度 B = 4.6×10⁻⁵ T，磁场方向沿水平方向由南向北，航天飞机和卫星的运行速度为 7.6 km/s。

（1）求导电缆绳中的感应电动势；

（2）导电缆绳的哪一端电势高？

参考解答：（1）7.2×10³ V

（2）由右手定则可知，感应电流方向由下向上，缆绳上端电势高，缆绳靠近绳系卫星一端的电势高。

5．如图所示，在与水平面成 θ = 30° 角的平面内放置两条平行、光滑且足够长的金属轨道，其电阻可忽略不计。空间存在着匀强磁场，磁感应强度 B = 0.20 T，方向垂直于轨道平面向上。导体棒 ab、cd 垂直于轨道放置，且与轨道接触良好构成闭合回路，每根棒的质量 m = 0.20 kg、电阻 r = 5.0×10⁻² Ω，轨道的宽度 l = 0.50 m。现对棒 ab 施加平行于轨道向上的拉力，在棒 ab 匀速向上运动的过程中，棒 cd 始终保持静止，取重力加速度 g = 10 m/s²。求：

（1）棒 cd 受到的安培力大小；

（2）棒 ab 运动的速度大小；

（3）拉力对棒 ab 做功的功率。

参考解答：（1）1 N

（2）10 m/s

（3）20 W

*6．某兴趣小组设计了一种发电装置，如图所示。在磁极和圆柱状铁芯之间形成的两磁场区域的圆心角 α 均为 \(\frac{4}{9}\) π，磁场均沿半径方向。匝数为 N 的矩形线圈 abcd 的边长 ab = cd = l，bc = ad = 2l。线圈以角速度 ω 绕中心轴匀速转动，bc 和 ad 边同时进入磁场。在磁场中，两条边所经处的磁感应强度大小均为 B，磁场方向始终与两边的运动方向垂直。线圈的总电阻为 r，外接小灯泡的电阻为 R。当线圈切割磁感线时，求：

（1）感应电动势的大小；

（2）bc 边所受安培力的大小。

参考解答：（1）E_m = 2NBl²ω

（2）F = \(\frac{{4{N^2}{B^2}{l^3}\omega }}{{R + r}}\)

发布时间：2022/8/19 上午10:55:36  阅读次数：2822