三、“复习与提高”参考答案与提示

通过章末习题加强对功、功率、动能、重力势能、弹性势能等基本概念的理解，巩固计算变力做功的方法，练习应用动能定理、机械能守恒定律、能量守恒定律分析解决实际问题，能将实际问题中的对象和过程转换成所学的物理模型，并运用能量守恒的观点对综合性物理问题进行分析和推理，获得结论作出解释。

A 组

1．6.3 m/s

提示：从将球向下抛出到球上升到最高点，小球减小的动能 ΔE_k = $\frac{1}{2}$mv₀²，小球增加的重力势能 ΔE_p = mgΔh，由机械能守恒定律有 ΔE_k = ΔE_p，解得 v₀ =  $\sqrt{2g\mathrm{\Delta }h}$ = $\sqrt{2\times 9.8\times 2}$ m/s = 6.3 m/s。

以小球先下降、后上升的往返运动为背景复习机械能守恒定律的简单应用。在应用机械能守恒定律分析解决问题时，只需考虑运动的初状态和末状态，不必考虑两个状态间过程的细节。

 

2．（1）2.4×10⁴ W；（2）4.8×10⁴ W

提示：（1）起重机匀加速上升的加速度a = $\frac{v}{t}$ = $\frac{4}{2}$ m/s² = 2 m/s²，由F − mg = ma 得起重机的牵引力 F = mg + ma = 1×10³×（10 + 2）N = 1.2×10⁴ N，起重机在 2 s 内上升的高度 h = $\frac{1}{2}$at² = 4 m，起重机在这 2 s 内的输出功率 P = $\frac{Fh}{t}$ = $\frac{1.2\times {10}^4\times 4}{2}$ W = 2.4×10⁴ W。

（2）起重机在 2 s 末的输出功率P = Fv = 1.2×10⁴×4 W = 4.8×10⁴ W。

以起重机将货物匀加速竖直吊起为情景，根据初、末速度和时间可求加速度、位移、平均速度，根据牛顿第二定律可求牵引力，根据功的定义或动能定理可求牵引力的功，根据 P = $\frac{W}{t}$ 或 P = Fv 可求功率，培养学生综合应用物理知识、从多个视角分析解决物理问题的能力。

 

 3．（1）如图 8–10 所示。

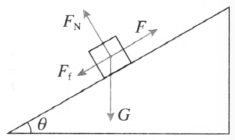
（2）F = mgcosθ，F_f = μF_N。重力做功 W_G = − mgxsinθ，推力做功 W_F = Fx，支持力做功 W_N = 0，摩擦力做功 W_f = − F_fx = − μmgxcosθ。

（3）总功 W_总 = W_F + W_G + W_f + W_N = Fx – mgxsinθ − μmgxcosθ。

（4）合力 F_合 = F – mgsinθ − μmgcosθ。

（5）合力做功 W_合 = F_合x = （F – mgsinθ − μmgcosθ）x，显然 W_总 = W_合。

 

4．$\frac{P}{v}$；$\frac{3P}{mv}$

提示：（1）当汽车的牵引力等于受到的阻力时，汽车达到最大速度，即 F = F_f。由 P = Fv 得行驶过程中汽车受到的阻力大小 F_f = F = $\frac{P}{v}$。

（2）当汽车的车速为 $\frac{v}{4}$ 时，汽车的牵引力 F = $\frac{4P}{v}$。由 F – F_f = ma 解得汽车的瞬时加速度的大小为 a = $\frac{3P}{mv}$。

 

5．（1）$\frac{v_0^2}{2g}$；（2）$\frac{v_0^2}{6g}$；（3）$\frac{v_0^2}{4g}$；（4）$\frac{v_0^2}{3g}$；（5）$\frac{3v_0^2}{8g}$

提示：（1）抛出时物体的机械能 E₀ = $\frac{1}{2}$mv₀²，物体上升到最高点时的机械能 E₁ = mgh，由机械能守恒定律可知 E₀ = E₁。联立解得 h = $\frac{v_0^2}{2g}$。

（2）物体的重力势能为动能的一半时的机械能 E₂ = mgh₁ + E_k1。由题设条件知 mgh₁ = $\frac{1}{2}$E_k1，再由机械能守恒定律知 E₀ = E₂。联立解得 h₁ = $\frac{v_0^2}{6g}$。

（3）物体的重力势能和动能相等时的机械能 E₃ = mgh₂ + E_k2。由题设条件知 mgh₂ = E_k2，再由机械能守恒定律知 E₀ = E₃。联立解得 h₂ = $\frac{v_0^2}{4g}$。

（4）物体的动能是重力势能的一半时的机械能 E₄ = mgh₃ + E_k3。由题设条件知 E_k3 =$\frac{1}{2}$mgh₃，再由机械能守恒定律知 E₀ = E₄。联立解得 h₃ = $\frac{v_0^2}{3g}$。

（5）物体的速率为 $\frac{v_0}{2}$ 时的机械能 E₅ = mgh₄ + $\frac{1}{2}$m($\frac{v_0}{2}$)²，由机械能守恒定律知 E₀ = E₅，联立解得 h₄ = $\frac{3v_0^2}{8g}$。

 

6．（1）$\frac{1}{2}$mv₁²；（2）$\frac{1}{2}$mv₂² − $\frac{1}{2}$mv₁² + 2mgR

提示：（1）物体由 A 到 B 的过程中机械能守恒，弹簧压缩至 A 时的弹性势能 E_p = $\frac{1}{2}$mv₁²。

（2）物体由 B 到 C 的过程中，阻力做功为 W_f，由动能定理知 − 2mgR + W_f = $\frac{1}{2}$mv₂² − $\frac{1}{2}$mv₁²，由此解得 W_f = $\frac{1}{2}$mv₂² − $\frac{1}{2}$mv₁² + 2mgR。

B 组

1．（1）mgl（1 − cosθ）；（2）$\sqrt{2gl(\sin \theta +\cos \theta -1)}$

提示：（1）小球从 P 点缓慢地移动到 Q 点的过程中，水平拉力 F 变大，由动能定理可知 W_F − mgl（1 − cosθ）= 0，解得 W_F = mgl（1 − cosθ）。

（2）小球在水平恒力 F = mg 的作用下从 P 点运动到 Q 点，故 Flsinθ − mgl（1 − cosθ）= $\frac{1}{2}$mv²，解得 v = $\sqrt{2gl(\sin \theta +\cos \theta -1)}$。

 

2．2∶1；4∶1

提示：由动能定理可知 W_A = 0 − $\frac{1}{2}$m_Av₀²，W_B = 0 − $\frac{1}{2}$m_Bv₀²，解得 $\frac{W_{\mathrm{A}}}{W_{\mathrm{B}}}$ = $\frac{m_{\mathrm{A}}}{m_{\mathrm{B}}}$ = $\frac{2}{1}$，由图 8–11 可知 A 的位移 x_A = $\frac{v_0}{2}$t，B 的位移 x_B = v₀t。又因 W_A = − F_Ax_A，W_B = − F_Bx_B。联立解得 $\frac{F_{\mathrm{A}}}{F_{\mathrm{B}}}$ = $\frac{W_{\mathrm{A}}{x}_{\mathrm{B}}}{W_{\mathrm{B}}{x}_{\mathrm{A}}}$ = $\frac{4}{1}$。

通过由动能定理求功、由速度图像求位移、由功的定义式求力，培养学生综合应用所学的物理知识解决实际问题的能力。

 

3．（1）7 536 m³/s；（2）1.63×10⁵ J/s；（3）1.63×10⁴ W

提示：（1）Δt 时间内冲击叶片圆面的气流的体积为 ΔV = SvΔt，又因 S = πr²，故 $\frac{\mathrm{\Delta }V}{\mathrm{\Delta }t}$ = vπr² = 7 536 m³/s。

（2）Δt 时间内冲击叶片圆面的气流的动能为 ΔE_k = $\frac{1}{2}$ρΔVv²，单位时间内气流的动能 $\frac{\mathrm{\Delta }{E}_{\mathrm{k}}}{\mathrm{\Delta }t}$ = $\frac{1}{2}$ρ$\frac{\mathrm{\Delta }V}{\mathrm{\Delta }t}$v² = 1.63×10⁵ J/s。

（3）风力发电机发电的功率 P = η$\frac{\mathrm{\Delta }{E}_{\mathrm{k}}}{\mathrm{\Delta }t}$ = 1.63×10⁴ W。

通过对风力发电情景的分析，培养学生建立流体模型的能力。

 

4．小木块在斜面上受到的滑动摩擦力 F₁ = μmgcosθ，在水平面上受到的滑动摩擦力 F₂ = μmg。整个过程中滑动摩擦力做功 W_f = − F₁$\frac{h}{\sin \theta }$ − F₂（x − $\frac{h}{\tan \theta }$），重力做功为 W_G = mgh，由动能定理得 W_G + W_f = 0，联立解得 x = $\frac{h}{\mu }$，x 与斜面倾角 θ 无关。

 

5．（1）l − $\frac{mg}{k}$；（2）mg（h + x）

提示：（1）铁球在下落过程中先加速后减速，当铁球速度最大（动能最大）时加速度为 0，此时弹簧的压缩量为 x₁，对小球有 mg – kx₁ = 0。铁球距地面的高度为 H = l – x₁，因此解得 H = l − $\frac{mg}{k}$。

（2）铁球下落到最低点时速度为 0，则铁球下落到高度为（h + x）处时，铁球的动能变化量为 0。根据机械能守恒定律，弹簧的弹性势能的增加量等于铁球重力势能的减少量，故铁球下落到最低点时，弹簧的弹性势能最大，大小为 mg（h + x）。

 

6．$\sqrt{\frac{2}{5}gh}$

提示：A 受到的拉力是 B 受到的拉力的两倍，A 上升。当 A 上升 h_A = h 时，B 下降 h_B = 2h，设此时 A、B 的速度分别为 v_A、v_B，则 v_B = 2v_A。再根据 A、B 组成的系统机械能守恒 mgh_B = mgh_A + $\frac{1}{2}$mv_A² + $\frac{1}{2}$mv_B²，解得 v_A = $\sqrt{\frac{2}{5}gh}$。

 

7．10¹⁰ J

提示：坝内水的质量 m = ρ（h₁ – h₂）S = 2.0×10⁹ kg，这一部分水的重力势能 E_p = mg $\frac{h_1-h_2}{2}$ = 2.0×10¹⁰ J。发电时减少的重力势能 ΔE_p = E_p − 0，一次落潮所发的电能 E = ηΔE_p = 0.5×2.0×10¹⁰ J = 10¹⁰ J。