第六章 圆周运动 复习与提高

图 6–2
A 组
1.请根据加速度的特点,对以下七种运动进行分类,并画出分类的树状结构图:匀速直线运动;匀变速直线运动;自由落体运动;抛体运动;平抛运动;匀速圆周运动;变速圆周运动。
2.图 6–1 是一皮带传动装置的示意图,右轮半径为 r,A 是它边缘上的一点。左侧是一轮轴,大轮半径为 4r,小轮半径为 2r。B 点在小轮上,到小轮中心的距离为 r。C 点和 D 点分别位于小轮和大轮的边缘上。如果传动过程中皮带不打滑,那么 A、B、C、D 点的线速度、角速度、向心加速度之比分别是多少?
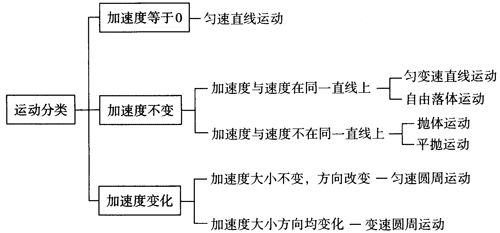
3.在空间站中,宇航员长期处于失重状态。为缓解这种状态带来的不适,科学家设想建造一种环形空间站,如图 6–2 所示。圆环绕中心匀速旋转,宇航员站在旋转舱内的侧壁上,可以受到与他站在地球表面时相同大小的支持力。已知地球表面的重力加速度为 g,圆环的半径为 r,宇航员可视为质点,为达到目的,旋转舱绕其轴线匀速转动的角速度应为多大?
4.如图 6–3 所示,长 L 的轻杆两端分别固
定着可以视为质点的小球 A、B,放置在光滑水平桌面上,杆中心 O 有一竖直方向的固定转动轴,小球 A、B 的质量分别为 3m、m。当轻杆以角速度 ω 绕轴在水平桌面上转动时,求转轴受杆拉力的大小。
5.如图 6–4 所示,滚筒洗衣机脱水时,滚筒绕水平转动轴转动。滚筒上有很多漏水孔,滚筒转动时,附着在潮湿衣服上的水从漏水孔
中被甩出,达到脱水的目的。如果认为湿衣服在竖直平面内做匀速圆周运动,那么,湿衣服上的水是在最低点还是最高点时更容易甩出?请说明道理。

6.波轮洗衣机中的脱水筒(图 6–5)在脱水时,衣服紧贴在筒壁上做匀速圆周运动。某洗衣机的有关规格如下表所示。在运行脱水程
| 型号 | ×× |
| 额定电压、频率 | ~ 220 V、50 Hz |
| 额定脱水功率 | 225 W |
| 质量 | 31 kg |
| 脱水转速 | 600 r/min |
| 脱水筒尺寸 | 直径 300 mm,高 370 mm |
| 外形尺寸 | 长 555 mm,宽 510 mm, 高 870 mm |
序时,有一质量 m = 6 g 的硬币被甩到桶壁上,随桶壁一起做匀速圆周运动。求桶壁对它的静摩擦力和弹力的大小。在解答本题时可以选择表格中有用的数据。g 取 10 m/s2。
7.如图 6–6 所示,半径为 R 的半球形陶罐,固定在可以绕竖直轴转动的水平转台上,转台转轴与过陶罐球心 O 的对称轴 OO′ 重合。转台以一定角速度匀速转动,一质量为 m 的小物块落入陶罐内,经过一段时间后小物块随陶罐一起转动且相对罐壁静止,此时小物块受到的摩擦力恰好为 0,且它和 O 点的连线与 OO′ 之间的夹角 θ 为 60°,重力加速度为 g。求转台转动的角速度。
B 组
1.如图 6–7 所示,半径 R = 0.40 m 的光滑半圆环轨道处于竖直平面内,半圆环与水平地面相切于圆环的端点 A。一小球从 A 点冲上竖直半圆环,沿轨道运动到 B 点飞出,最后落在水
平地面上的 C 点(图上未画),g 取 10 m/s2。
(1)能实现上述运动时,小球在 B 点的最小速度是多少?
(2)能实现上述运动时,A、C 间的最小距离是多少?
2.如图 6–8 所示,做匀速圆周运动的质点在时间 t 内由 A 点运动到 B 点,\(\overset{\frown}{AB}\) 所对的圆心角为 θ,\(\overset{\frown}{AB}\) 长为 l,
(1)求质点向心加速度的大小。
(2)若某段时间内 θ = 60°,根据矢量的运算
法则,求这段时间内 \(\frac{{\Delta v}}{{\Delta t}}\) 与圆周运动的向心加速度的大小之比是多少?
3.如图 6–9 所示,带有一白点的灰色圆盘,绕过其中心且垂直于盘面的轴沿顺时针方向匀速转动,转速 n = 20 r/s。在暗室中用每秒闪光 21 次的频闪光源照射圆盘,求观察到白点转动的方向和转动的周期。
4.如图 6–10 所示,一长为 l 的轻杆的一端固定在水平转轴上,另一端固定一质量为 m 的小球,轻杆随转轴在竖直平面内做角速度为 ω 的匀速圆周运动,重力加速度为 g。
(1)小球运动到最高点时,求杆对球的作用力。
(2)小球运动到水平位置 A 时,求杆对球的作用力。
5.如图 6-11 所示,质量为 m 的小球用细线悬于 – 点,使小球在水平面内做匀速圆周运动,重力加速度为 g。
(1)若悬挂小球的绳长为 l,小球做匀速圆周运动的角速度为 ω,绳对小球的拉力 F 有多大?
(2)若保持轨迹圆的圆心 O 到悬点 P 的距离 h 不变,改变绳长 l,求小球做匀速圆周运动
的角速度 ω 与绳长 l 的关系。
(3)若保持轨迹圆的圆心 O 到悬点 P 的距离 h 不变,改变绳长 l,求绳对 A 球的拉力 F 与绳长 l 的关系。
6.某人站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为 m 的小球,使球在竖直平面内以手为圆心做圆周运动。当球某次运动到最低点时,绳恰好受到所能承受的最大拉力被拉断,球以绳断时的速度水平飞出,通过水平距离 d 后落地。已知握绳的手离地面高度为 d,手与球之间的绳长为 \(\frac{d}{4}\),重力加速度为 g,忽略空气阻力。
(1)绳能承受的最大拉力是多少?
(2)保持手的高度不变,改变绳长,使球重复上述运动,若绳仍在球运动到最低点时达到最大拉力被拉断,要使球抛出的水平距离最大,绳长应是多少?最大水平距离是多少?
7.某场地自行车比赛圆形赛道的路面与水平面的夹角为 15°,sin15° = 0.259,cos15° = 0.966,不考虑空气阻力,g 取 10 m/s2。
(1)运动员骑自行车在该赛道上做匀速圆周运动(图 6–12),圆周的半径为 60 m,要使自行车不受摩擦力作用,其速度应等于多少?
(2)若该运动员骑自行车以 18 m/s 的速度仍沿该赛道做匀速圆周运动,自行车和运动员的质量一共是 100 kg,此时自行车所受摩擦力的大小又是多少?方向如何?

复习与提高”参考答案与提示
A、B 两组共 14 道习题,大致可分为三个层次。
第一层次的习题。让学生系统理解与圆周运动相关的物理概念和规律,形成物理观念,并进行科学推理。如让学生用思维导图理解、并对运动进行分类,计算圆周运动各个物理量的规律及其相互关系,进行向心加速度方向和公式的理论推导。
第二层次的习题。将各种实际问题转换为一个或者多个物理模型,通过计算推理得出结论,培养学生的科学思维、探究精神,让学生逐步形成对身边观察到的现象进行抽象进而应用物理规律解决实际问题的科学态度。如在空间站中模拟重力,两种洗衣机脱水过程的受力分析,频闪照相中匀速圆周运动的追击问题,圆周运动径向连接体问题,水平面内圆锥摆问题,与平抛运动结合的竖直面内圆周运动的临界问题。
第三层次的习题。练习将实际问题中的对象转换成物理模型的能力,对综合性问题进行分析推理获得结论,并采用不同的方式对同一问题进行分析论证,对学生的能力要求较高。如水平面内圆锥摆问题,杆连接体竖直面内的圆周运动,将竖直面内圆周运动和平抛运动结合并讨论平抛运动的极值问题,场地自行车问题中正交分解法的灵活应用。
A 组
1.如图 6–25 所示。
2.vA∶vB∶vC∶vD = 2∶1∶2∶4,ωA∶ωB∶ωC∶ωD = 2∶1∶1∶1,aA∶aB∶aC∶aD = 4∶1∶2∶4。
提示:在皮带传动中,同轴转动的角速度大小相等。同一皮带轮缘的线速度大小相等,以此为突破口分析线速度、角速度与半径之间的关系,向心加速度与线速度和角速度之间的关系。
3.参考解答:\(\sqrt {\frac{g}{r}} \)
提示:宇航员站在地球表面时有 FN = mg,要使宇航员站在旋转舱内圆柱形侧壁上,受到与他站在地球表面时相同大小的支持力,则 FN = mrω2,由此解得 ω = \(\sqrt {\frac{g}{r}} \)。
4.mω2L
提示:小球 A 受到重力、支持力和杆向右的拉力 FA,根据牛顿第二定律有 FA = \(\frac{{3m{\omega ^2}L}}{2}\)。小球 B 受到重力、支持力和杆向左的拉力 FB,根据牛顿第二定律有 FB = \(\frac{{m{\omega ^2}L}}{2}\)。根据牛顿第三定律,小球 A 对杆的拉力大小 FAʹ = FA = \(\frac{{3m{\omega ^2}L}}{2}\),方向水平向左。小球 B 对杆的拉力大小 FBʹ = FB = \(\frac{{m{\omega ^2}L}}{2}\),方向水平向右。轻杆受 FAʹ、FBʹ、转轴对杆的拉力 F,根据平衡条件得 FAʹ = F + FBʹ,由此解得 F = mω2L,方向向右。根据牛顿第三定律,杆对转轴的拉力大小,Fʹ = F = mω2L。
本题从运动学角度看连接的各物体有相同的角速度、周期和圆心,从力学角度看彼此间通过轻杆有拉力相互作用,解题的关键是明确研究对象,用隔离法进行正确的受力分析,列方程求解。
5.滚筒洗衣机的脱水筒匀速旋转时,附着在筒壁上的衣服做圆周运动的向心力由重力和弹力提供。衣服在最高点时,附着在潮湿衣服上的水的重力和衣服与水之间的分子力的合力提供向必力。对比最高点和最低点水的受力情况可知,在同一转速的情况下,水在最低点所受到的分子力更大,所以更容易在最低点从漏水孔甩出,做离心运动。
参考解答:滚筒洗衣机的脱水桶匀速旋转时,附着在桶壁上的衣服做匀速圆周运动的向心力由重力和弹力提供。衣服在最高点时,附着在潮湿衣物上的水的重力和衣服与水之间的分子力的合力提供向心力。对比最高点和最低点水的受力情况可知,在同一转速的情况下,水在最低点所受到的分子力更大,所以更容易在最低点从漏水孔甩出,做离心运动。
6.0.06 N;3.55 N
提示:分析硬币的受力情况如图 6–26 所示。
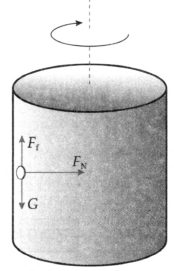
由表格中的数据可知,脱水桶的转速 n = 600 r/min =10 r/s,脱水桶的直径 D = 0.3 m,则半径 r = 0.15 m。在水平方向由弹力提供向心力,即 FN = mω2r,得 FN = 3.55 N。
在竖直方向上,摩擦力与重力平衡,故 Ff = G = 0.06 N。
让学生分析并计算生活中常见的波轮洗衣机中物体的受力情况,以培养学生应用理论知识解决实际问题的能力。
参考解答:0.06 N;3.55 N。
7.参考解答:\(\sqrt {\frac{{2g}}{R}} \)
提示:小物块不受摩擦力,由重力和支持力的合力提供向心力。小物块在水平面内做匀速圆周运动,故其半径为 Rsin60°,再根据向心力公式求得 ω = \(\sqrt {\frac{{2g}}{R}} \)。
B 组
1.(1)2 m/s;(2)0.8 m
提示:(1)小球在 B 点速度最小时,小球与半圆环轨道间的弹力恰好等于 0,此时小球仅受竖直向下的重力作用,根据牛顿第二定律有 mg = \(\frac{{v_{\min }^2}}{r}\),解得 vmin = \(\sqrt {gR} \) = 2 m/s。
(2)小球从 B 点水平飞出后做平抛运动,小球以最小速度平抛时距离最小,设小球做平抛运动的时间为 t,AC 间最小距离为 x,则水平方向有 x = vt,竖直方向有 2R = \[\frac{1}{2}\]gt2。由此解得 t = 0.4 s,x = 0.8 m。
参考解答:(1)2 m/s;(2)0.8 m
2.(1)\(\frac{{l\theta }}{{{t^2}}}\);(2)\(\frac{{\Delta v}}{t}\)
提示:(1)质点做圆周运动的半径 r = \(\frac{l}{\theta }\),角速度 ω = \(\frac{\theta }{t}\),向心加速度的大小 an = rω2 = \(\frac{{\Delta v}}{t}\)。
(2)如图 6–27 甲所示,设物体在 A 点时速度为 vA,经过很短的时间 Δt 运动到 B 点,速度为 vB,转过的角度为 θ,速度变化量 Δv = vB – vA,如图 6–27 乙所示。

比值 \(\frac{{\Delta v}}{{\Delta t}}\) 是物体在 Δt 时间内的平均加速度,方向与 Δv 的方向相同。当 Δt 趋近于 0 时,\(\frac{{\Delta v}}{{\Delta t}}\) 就表示物体在 A 点的瞬时加速度。在图示的矢量三角形中,vA = vB = v。当 Δt 趋近于 0 时,θ 也趋近于 0,Δv 的方向趋近于跟 vA 垂直,且指向圆心,所以向心加速度的方向沿半径指向圆心。由以上分析可知,向心加速度大小 an = \(\frac{{\Delta v}}{t}\)。
向心加速的方向和公式的推导是一个难点内容,本题用三角形法则较好地突破了速度与速度变化量的方向关系的难点,并结合极限思想推导向心加速度公式,加强用数学工具解决物理问题的训练,培养学生严谨的科学态度和科学推理能力。
3.观察到白点逆时针转动,周期为 1 s。
提示:圆盘转动一周所需要的时间为 T1 = \(\frac{1}{{20}}\) s,频闪光源每隔 T2 = \(\frac{1}{{21}}\) s 闪一次,所以频闪光源每闪一次,白点尚未运动一周,故观察到白点逆时针转动。每次闪光,白点与原位置相差的角 Δθ = 2π – ω1T2 = 2π − \(\frac{{2\pi }}{{{T_1}}}\)×T2 = \(\frac{{2\pi }}{{21}}\),所以白点转动的周期 T = \(\frac{{2\pi }}{\omega }\) = \(\frac{{2\pi }}{{\frac{{\Delta \theta }}{{{T_2}}}}}\) = 1 s。
本题实际上是两个质点以不同的角速度做匀速圆周运动的追击问题,即 \(\frac{1}{T}\) = \(\frac{1}{{{T_1}}}\) − \(\frac{1}{{{T_2}}}\) = n2 – n1。学生在分析问题时,会错误地认为频闪比圆盘转动的快,看到白点的转动会更快,其实应当分析每次闪光时白点所在位置的变化才能判断白点转动的方向,并计算出白点转动的周期。
参考解答:观察到白点逆时针转动,周期为 1 s。
4.(1)因转动的角速度大小未知,故小球在最高点时,杆对球的作用力 F1 方向不能确定。假设 F1 的方向竖直向下。根据 F1 + mg = mω2l 解得 F1 = m(ω2l − g)。
若 ω>\(\sqrt {\frac{g}{l}} \),杆对小球的拉力大小为 F1 = m(ω2l − g),方向竖直向下。
若 ω =\(\sqrt {\frac{g}{l}} \) ,F1 = 0,杆对小球恰好无作用力。
若 ω<\(\sqrt {\frac{g}{l}} \),杆对小球的支持力大小为 F1 = m(g − ω2l),方向竖直向上。
(2)小球运动到水平位置 A 处时,杆对球的竖直方向分力 Fy = mg,水平方向分力 Fx = mω2l,故杆对球的作用力大小 F2 = \(\sqrt {F_x^2 + F_y^2} \) = \(\sqrt {{m^2}{\omega ^4}{l^2} + {m^2}{g^2}} \)。设该作用力与水平方向夹角为 θ,则有 tanθ = \(\frac{{{F_x}}}{{{F_y}}}\) = \(\frac{{mg}}{{m{\omega ^2}l}}\) = \(\frac{g}{{{\omega ^2}l}}\)。
故在位置 A 处杆对小球的作用力方向斜右向上,与水平方向夹角为 θ = arctan\(\frac{g}{{{\omega ^2}l}}\)。
提示:对于竖直平面内的圆周运动,注意,要注意在最高点,杆对球的作用力可能是拉里,也可能是支持力,还可能无作用力。通过分类讨论,以培养学生的发散思维和全面分析问题的能力。第(2)问求在A点杆对球的作用力时,要注意该作用力是杆对球在水平和竖直两个方向的分力的合力。
5.(1)mω2l;(2)ω 与 l 无关;(3)成正比
提示:(1)如图 6–28 甲所示,小球受到重力和沿细绳方向的拉力,设细绳与竖直方向的夹角为 θ。沿水平方向轴方向有 Fn = Fsinθ = mω2lsinθ,解得细绳对小球的拉力 F = mω2l。
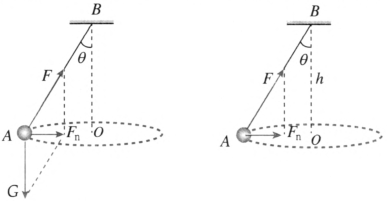
(2)如图 6–28 乙所示,小球受到重力和细绳拉力的合力指向圆心,有 mgtanθ = mω2htanθ,解得 ω = \(\sqrt {\frac{g}{h}} \)。可见,轨迹圆的圆心 O 到悬点 B 的距离 h 不变,改变绳长 l 时,角速度 ω 保持不变,与绳长 l 无关。
(3)由第(1)(2)两问的结论 F = mω2l 和 ω = \(\sqrt {\frac{g}{h}} \),解得 F = \(\frac{{mgl}}{h}\),细绳的拉力 F 与绳长 l 成正比。
参考解答:(1)mω2l;(2)ω 与 l 无关;(3)成正比
6.(1)\(\frac{{11}}{3}\)mg;(2)绳长为 \(\frac{{d}}{2}\),最大水平距离为 \(\frac{{2d}}{{\sqrt 3 }}\)
提示:(1)已知手与球之间的绳长为 \(\frac{{d}}{4}\),平抛的水平位移为 d,设小球在最低点时绳能承受的最大拉力为 Fmax,根据向心力公式和平抛运动规律,有 Famx – mg = ,d = vt,d − \(\frac{{d}}{4}\) = \(\frac{{1}}{2}\)gt2。由此解得 Fmax = \(\frac{{11}}{3}\)mg。
(2)如图 6–29 所示,设手与球之间的绳长为 r,平抛的水平位移为 x,由第 1 问可知绳能承受的最大拉力为 Fmax = \(\frac{{11}}{3}\)mg,根据向心力公式和平抛运动规律,有 Fmax – mg = \(\frac{{m{v^2}}}{r}\),x = vt,d – r = \(\frac{{1}}{2}\)gt2,由此解得 Fmax = mg + \(\frac{{{x^2}}}{{2r(d - r)}}\)。当 Fmax = \(\frac{{11}}{3}\)mg 时,代入上式有 x2 = \(\frac{{16}}{3}\)r(d − r),则当 r = \(\frac{{d}}{2}\) 时,xmax = \(\frac{{2d}}{{\sqrt 3 }}\)。
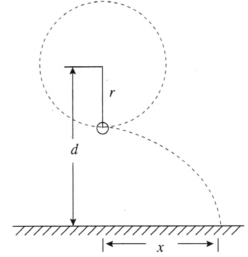
根据临界状态下圆周运动和平抛运动表达式求解最大拉力,并进一步建立二次函数表达式进行分析讨论,体现数理结合的方法。
7.(1)12.7 m/s;(2)263 N,方向沿着倾斜路面指向内侧
提示:(1)自行车恰好不受摩擦力时,运动员和自行车所受重力及赛道支持力的合力提供向心力,根据牛顿第二定律有 mgtan15° = m\(\frac{{v_0^2}}{r}\),解得 v0 = \(\sqrt {gr\tan 15^\circ } \) = 12.7 m/s。
(2)运动员骑自行车以 v1 = 18 m/s 做匀速圆周运动时,因 v1 > v0,故赛道给自行车的静摩擦力 Ff 沿斜面向下,受力分析如图 6–30 所示。
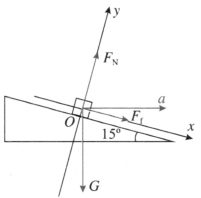
在 x 轴方向由牛顿第二定律可知 Ff + mgsin15° = ma。将自行车水平加速度沿 x 轴分解得 ax = acos15°,再根据向心加速度公式 a = \(\frac{{{v^2}}}{r}\),联立解得 v = 5.4 m/s,ax = 5.22 m/s2,Ff = 263 N。
摩擦力方向沿着倾斜路面指向内侧。
以场地自行车比赛圆形赛道为背景,在新的情景中巩固处理火车转弯问题的思路和方法。当恰好无摩擦力时,赛道的支持力和重力的合力提供向心力,当圆周运动的速度超过临界速度时,向心力增大,使赛道提供向内的静摩擦力。实际上,场地自行车赛道并不是圆形,各处的坡度和对应的曲率半径也不相同,所以应是特指在赛道上的某一处,且不能说做匀速圆周运动。
发布时间:2022/8/10 上午10:48:19 阅读次数:4974
