第五章 抛体运动 复习与提高
A 组
1.物体在平面上的位置和位移常用平面直角坐标系来表示。图 5–1 是中国象棋的棋盘,它相当于一个平面直角坐标系,横坐标上标有数字,纵坐标上标有字母。利用它不仅可以准确地记录各棋子的位置,还能描述棋子的位移,从而能将双方对弈的过程记录下来。例如,棋子“帅”位于 y = J、x = 5 的位置,可以简述为 J5 ;棋子“象”从 y = A、x = 3 的位置运动到 y = C、x = 5 的位置,就可以简述为 A3C5。
(1)还未开局时,甲方的马在 J2 和 J8 的位置、炮在 H2 和 H8 的位置、中兵在 G5 的位置,乙方的中兵在 D5 的位置,请你在棋盘上标明这六个棋子的位置。
(2)某次甲方开局时,用“当头炮”,即 H8H5, 而乙方的应变则 是“马来跳”,即 A2C3。请你用带箭头的线段画出这两个位移 l甲和 l乙 ,并指出这两个位移在 x、y 方向上的分位移各是多少?已知棋盘每个小方格都是边长为 3 cm 的正方形。

2.某质点从 A 点沿图 5–2 中的曲线运动到 B 点,质点受力的大小为 F。经过 B 点后,若力的方向突然变为与原来相反,它从 B 点开始可
能沿图中的哪一条虚线运动?为什么?

3.某架飞机在进行航空测量时,需要严格按照从南到北的航线进行飞行。如果在无风时飞机相对地面的速度是 414 km/h,飞行过程中航路上有速度为 54 km/h 的持续东风。
(1)飞机应该朝着哪个方向飞行?可以用三角函数表示偏角的大小。
(2)如果所测地区的南北长度为 621 km,该测量需要多长时间?
4.在水平路面上骑摩托车的人,遇到一个壕沟,其尺寸如图 5–3 所示。摩托车后轮离开地面后失去动力,可以视为平抛运动。摩托车后轮落到壕沟对面才算安全。摩托车的速度至少要多大才能越过这个壕沟? g 取 10 m/s2。

5.一架飞机水平匀速飞行,搭载着多名高空跳伞运动员。每隔 1 s 有一名运动员从飞机上落下。粗略画出第四名运动员刚离开飞机时,飞机和他们在空中的位置情况,此时相邻两运
动员在竖直方向上的距离之比依次是多少?这段时间内伞没有打开,可忽略空气阻力。
6.如图 5–4 所示,在一端封闭的光滑细玻璃管中注满清水,水中放一个由蜡做成的小圆柱体 R。R 从坐标原点以速度 v0 = 1 cm/s 匀速上浮的同时,玻璃管沿 x 轴正方向做初速度为 0 的匀加速直线运动。测出某时刻 R 的 x、y 坐标值分别为 6 cm 和 2 cm。求此时 R 的速度的大小。
7.跳台滑雪是一项勇敢者的滑雪运动,运动

员穿专用滑雪板,在滑雪道上获得一定速度后从跳台飞出,在空中飞行一段距离后着陆。现有某运动员从跳台 A 处沿水平方向飞出,在斜坡 B 处着陆,如图 5–5 所示。测得 A、B 间的距离为 40 m,斜坡与水平方向的夹角为 30°,试计算运动员在 A 处的速度大小和在空中飞行的时间。不计空气阻力,g 取 10 m/s2。
有兴趣的同学可以计算一下运动员在空中离坡面的最大距离。

B 组
1.在篮球比赛中,投篮的投出角度太大和太小,都会影响投篮的命中率。在某次投篮表演中,运动员在空中一个漂亮的投篮,篮球以与水平面成 45°的倾角准确落入篮筐,这次跳起投篮时,投球点和篮筐正好在同一水平面上(图 5–6),设投球点到篮筐距离为 9.8 m,不考虑空气阻力。

(1)篮球进筐的速度有多大?
(2)篮球投出后的最高点相对篮筐的竖直高度是多少?
2.环保人员在一次检查时发现,有一根排污管正在向外满口排出大量污水。这根管道水平设置,管口离地面有一定的高度,如图 5–7 所示。现在,环保人员只有一把卷尺,请问需要测出哪些数据就可大致估测该管道的排污量?写出测量每秒钟排污体积的表达式。

3.在某次演习中,轰炸机沿水平方向投放了一枚炸弹,炸弹正好垂直击中山坡上的目标,山坡的倾角为 θ,如图 5–8 所示。不计空气阻力,求炸弹竖直方向下落的距离与水平方向通过的距离之比。

4.一小球从空中某点水平抛出,经过 A、B 两点,已知小球在 A 点的速度大小为 v1、方向与水平方向成 30° 角,小球在 B 点的速度方向与水平方向成 60° 角。不计空气阻力,重力加速度为 g,求小球由 A 到 B 的运动时间及 A、B 两点间的距离。

5.如图 5–9,质量为 m 的质点在 Oxy 平面坐标系上以某一速度(如图中箭头方向)运动时,受到大小不变、方向为 − y 方向的合力作用,质点的
速度先减小后增大。已知质点运动的最小速度为 v,恒力的大小为 F。
(1)当质点速度大小变为 2v 时,速度方向和 x 方向之间的夹角是多大?
(2)质点速度由 v 增加到 2v 的过程用了多少时间?
6.某质点在 Oxy 平面上运动。t = 0 时,质点位于 y 轴上。它在 x 方向运动的速度-时间图像如图 5–10 甲所示,它在 y 方向的位移-时间图像如图 5–10 乙所示。
(1)求 t = 0.5 s 时质点速度的大小和方向。
(2)说出 t = 0.5 s 时质点的位置。
(3)在平面直角坐标系上大致描绘质点在 2 s 内的运动轨迹。

“复习与提高”参考答案与提示
通过章末习题加强对曲线运动、运动的合成与分解、平抛运动等基本概念的理解和应用,在中国象棋、飞机飞行、摩托车飞跃壕沟、跳伞、跳台滑雪、蜡块运动、投篮、估测排污量、飞机投弹等一系列实际问题中,练习模型建构,进行推理和论证,进一步巩固所学曲线运动的知识和方法,并能将运动的合成与分解、平抛运动的思想方法进行迁移,处理较复杂的实际问题。
A 组
1.(1)棋盘上六个棋子的位置如图 5–25 所示。

(2)位移 l甲 和 l乙 如图 5-26 所示,l甲 = − 3×3 cm = − 9 cm。

甲在 x 方向的分位移为 − 9 cm,方向与 x 轴正方向相反,在 y 方向的位移为 0。
l乙 = \(\sqrt {{3^2} + {{(2 \times 3)}^2}} \) cm= 3\(\sqrt 5 \) cm。
乙在 x 方向的分位移为 3 cm,方向与 x 轴正方向相同,在 y 方向的位移为 − 6 cm,方向与 y 轴正方向相反。
提示:本题练习将实际问题中的对象和过程转换成物理模型的能力,将棋子看作质点,将棋子的移动用位移描述,理解合运动与分运动的关系。
2.可能沿虚线 a 运动。
质点由 A 点运动到 B 点,F 方向为指向曲线弯折方向。在 B 点,速度方向为过 B 点的切线方向,经过 B 点后,质点受到的力 F 反向后,轨迹将向合力 F 的方向弯曲,故可能沿虚线 a 运动。
提示:本题复习质点的速度方向、合力方向和轨迹的弯曲方向之间的关系,加深对力和运动的关系的理解。
3.(1)飞机飞行的方向如图 5–27 所示。
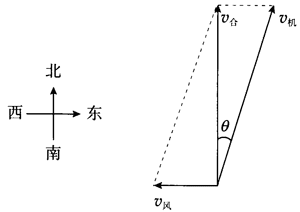
由题意得 sinθ = \(\frac{{{v_风}}}{{{v_机}}}\) = \(\frac{54}{414}\) = \(\frac{2}{23}\),所以飞机应朝北偏东 θ 角的方向行驶。
(2)由题意可知 v合 = v机cosθ = v机\(\sqrt {1 - {{\sin }^2}\theta } \) = 414×\(\sqrt {1 - {{(\frac{3}{{23}})}^2}} \) km/h ≈ 410 km/h,故飞行时间 t = \(\frac{{{x}}}{{{v_合}}}\) ≈ 1.5 h。
4.摩托车的速度至少要达到 15.8 m/s 才能越过壕沟。
5.四名运动员和飞机的位置如图 5–28 所示,他们在竖直方向的距离之比依次为 5∶3∶1。
提示:如图 5–28 所示,在竖直方向,根据 h = \(\frac{1}{2}\)gt2,可得 h12∶h23∶h34 =(32 – 22)∶(22 – 12)∶12 = 5∶3∶1。

6.圆柱体 R 的速度为 \(\sqrt {37} \) cm/s。
提示:根据运动的分解可知 y = v0t,x = \(\frac{{{v_x}}}{2}\)t,由此解得 vx = \(\frac{{2x}}{y}\) v0 = 6 cm/s。此时 R 的速度 v = \(\sqrt {v_0^2 + v_x^2} \) = \(\sqrt {37} \) cm/s。
7.运动员在 A 处的速度为 10\(\sqrt {3} \) m/s,茌空中飞行的时间为 2 s。
B 组
1.(1)9.9 m/s;(2)2.45 m
提示:(1)设篮球出手和进筐的速度大小分别为 v0 和 v,由题意可知 v = v0。设篮球从出手到落人篮筐所用的时间为 t,在竖直方向篮球只受重力,为竖直上抛运动,有 – v0sin 45° = v0sin45° − gt。篮球在水平方向的分运动为匀速运动,有 x = v0tcos45°。联立解得 v = \(\sqrt {98} \) m/s ≈ 9.9 m/s。
(2)篮球投出后的最高点相对篮筐的竖直高度 h = \(\frac{{{{({v_0}\sin 45^\circ )}^2}}}{{2g}}\) = 2.45 m。
2.需测量管口的直径 D,水平方向的位移 L,竖直方向的位移 h。每秒排出污水的体积为 V = \(\frac{{\pi {D^2}L}}{4}\sqrt {\frac{g}{{2h}}} \)。
提示:设水从管口落到地面的时间为 t,竖直方向的位移为 h,水平方向的位移为 L,则有 h = \(\frac{1}{2}\)gt2,L = vt。设管口直径为 D,联立解得 V = \(\frac{{\pi {D^2}L}}{4}\sqrt {\frac{g}{{2h}}} \)。
可见,需要测量 D、L、h。
3.\(\frac{1}{{2\tan \theta }}\)。
提示:平抛的末速度与竖直方向的夹角等于斜面倾角 θ,有 tanθ = \(\frac{{{v_0}}}{{gt}}\)。下落高度与水平射程之比 \(\frac{y}{x}\) = \(\frac{{g{t^2}}}{{2{v_0}t}}\) = \(\frac{{gt}}{{2{v_0}}}\) = \(\frac{1}{{2\tan \theta }}\)。
4.t = \(\frac{{{v_1}}}{g}\),\(\frac{{\sqrt 7 v_1^2}}{{2g}}\)
提示:小球运动轨迹如图 5–29 所示。

A 点的竖直分速度 vAy = v1sin30°,水平分速度 v0 = v1cos30°,B 点的竖直分速度 vBy = v0tan60°,小球从 A 到 B 的运动时间 t = \(\frac{{{v_{By}} - {v_{Ay}}}}{g}\),由此解得小球从 A 到 B 的运动时间 t = \(\frac{{{v_1}}}{g}\) 。因 A、B 间的水平距离 x = v0t = \(\frac{{\sqrt 3 v_1^2}}{{2g}}\)。A、B 间的竖直距离 y = \(\frac{{v_{By}^2 - v_{Ay}^2}}{{2g}}\) = \(\frac{{v_1^2}}{g}\),故 A、B 两点间的距离 s = \(\sqrt {{x^2} + {y^2}} \) = \(\frac{{\sqrt 7 v_1^2}}{{2g}}\)。
5.60°;\(\frac{{\sqrt 3 mv}}{F}\)
提示:质点沿 x 轴方向的分运动为匀速运动,沿 y 轴方向的分运动为先沿正方向做匀减速运动后,再沿负方向做匀加速运动。在最高点仅具有沿 x 轴方向的分速度 v0x,则 v0x = v。
(1)当质点速度大小变为 v′ = 2v 时,设速度方向和 x 轴正方向之间的夹角为 θ,则 cosθ = \(\frac{{{v_{0x}}}}{{v'}}\) = \(\frac{v}{2v}\) = \(\frac{1}{2}\),即 θ = 60°。
(2)vy = \(\sqrt {{{(2v)}^2} - {v^2}} \) = \(\sqrt 3 \)v,vy = at,a = \(\frac{F}{m}\)。由此解得 t = \(\frac{{\sqrt 3 mv}}{F}\)。
6.(1)5\(\sqrt 2 \) m/s,方向与 x 轴正方向的夹角为 45°,斜向第四象限;
(2)质点的位置坐标为(2.25 m,7.5 m);
(3)轨迹如图 5–30 所示
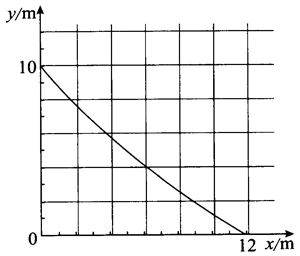
(1)由 v–t 图像可知,在石轴上质点做初速为 v0x = 4 m/s 的匀加速直线运动,加速度为 ax = \(\frac{{\Delta v}}{{\Delta t}}\) = 2 m/s2。在时刻 t,沿 x 轴的分速度为 vx = v0x + axt = (4 + 2t)m/s,方向沿 x 轴正方向。
由 y–t 图像可知,质点在 y 轴上做匀速直线运动,沿 y 轴的分速度为 vy = \(\frac{{\Delta y}}{{\Delta t}}\) = − 5 m/s,方向沿 y 轴负方向。故当 t = 0.5 s 时,v = \(\sqrt {v_0^2 + v_y^2} \) = 5\(\sqrt 2 \) m/s,tanθ = \(\frac{{{v_y}}}{{{v_x}}}\) = 1。该时刻质点速度方向与 x 轴正方向的夹角为 45°,斜向第四象限。
(2)质点在 x 轴上的位置坐标 x = v0t + \(\frac{1}{2}\)axt2,在 y 轴上的位置坐标 y = y0 + vyt。将 t = 0.5 s、v0x = 4 m/s、a = 2 m/s2、vy = 5 m/s 代入,解得 x = 2.25 m,y = 7.5 m。故当 t = 0.5 s 时,质点的位置坐标为(2.25 m,7.5 m)。
发布时间:2022/8/6 下午4:20:03 阅读次数:4908
