第 2 节  运动的合成与分解 教学参考

1．教学目标

（1）会根据研究问题的需要建立合适的平面直角坐标系，并用函数描述直线运动。

（2）理解合运动与分运动的概念，能对简单平面运动进行合成与分解。

（3）通过运动的合成与分解，初步体会把复杂运动分解为简单运动的物理思想，并能用这个思想解决类似的简单问题。

2．教材分析与教学建议

本节对学生的能力要求较高，着重要解决的问题是让学生建立起运动的合成与分解的思想，并用来处理简单的平面运动，为平抛与斜抛运动的研究打好基础。本节内容是学生在学习较简单的直线运动后，从定量研究直线运动规律进入定量研究曲线运动规律的转折点。虽然学生已经知道曲线运动的运动特征和受力特征，但他们不知道如何去描述曲线运动的位移、速度、加速度等运动参量。在此之前，学生已经有合力与分力的概念，力的合成与分解的知识与思想，这些对运动的合成与分解有一定的启发作用。通过本节的学习研究，学生将学会用平面坐标系描述曲线运动，并通过运动的合成与分解，把复杂运动分解成几个简单的分运动，再通过研究分运动的性质来确定物体实际运动的性质和轨迹，进一步研究复杂的曲线运动。

（1）平面运动的实例分析

教材以人在流动的河水中游泳是否能到达河的正对岸这一问题切入，引出蜡块运动实验。由蜡块运动引出合运动的概念，并引导学生猜测蜡块运动的轨迹与运动性质，尝试建立坐标系进行研究。依据蜡块沿玻璃管向上运动与随玻璃管一起水平向右匀速运动的现象，在这两个方向上建立直角坐标系。由于蜡块在这两个方向上的运动分别是匀速直线运动，可以用已有的直线运动规律进行描述，并由此得到轨迹函数和蜡块运动的速度。这样分析蜡块的运动就为合运动与分运动的教学做好了铺垫。教材的编排以情境发展为主线，主要包括“情境体验→实验探究→理论分析”等教学环节，通过逐步推进来实现运动合成与分解的知识构建。这样的编排有利于学生科学思维素养的培养。

蜡块运动实验是本节的重点之一。合运动与分运动两个概念的建立，坐标系的建立、蜡块运动轨迹的探究、蜡块运动速度的探究都基于本实验，因此教师一定要精心准备，确保实验成功。运动合成与分解知识的构建、运动等效思想是本节的另一个重点。

教材中设置了一个问题情境和一个演示实验来展开物体在平面中运动的研究，引出如何描述平面上运动物体的运动轨迹、位移、速度、加速度等问题。这样的安排有助于学生从已有知识出发，去发现新问题，形成探究的意向与目标，为解决新的问题做好准备。实验演示要与学生的思考紧密结合。例如要观察蜡块的运动方向，蜡块的运动轨迹，思考蜡块的运动性质，思考合运动与分运动之间的关系等。

教学片段

探究合运动与分运动的关系

蜡块的运动如图 5–12 所示，蜡块运动的视频截图如图 5–13 所示。

问题 1．在图 5–12 丙中，蜡块同时参与了哪几个运动？蜡块实际的运动是怎样的？

问题 2．合运动与分运动所用的时间有什么关系？

问题 3．如图 5–13，改变玻璃管在水平方向运动的速度，蜡块从 A（底部）到 B（顶端）的运动时间会变吗？玻璃管在水平方向的运动变化会不会影响蜡块在竖直方向的运动？

问题 4．根据图 5–13，你能画出分运动与合运动的位移吗？它们之间满足什么关系？

问题 5．根据合运动和分运动的等时性，你觉得合速度与分速度之间是否也满足上述关系？

问题 6．飞机起飞时的速度为 300 km/h，飞行方向与水平面的夹角为 30°，水平分速度和竖直分速度各是多大？

问题 7．一艘炮舰沿河由西向东匀速行驶，在炮舰上发射炮弹，要击中正北岸的目标。能直接向正北方向发射炮弹吗？

---

做好实验是上好本课的关键。实验时，教师要提醒学生，这里的研究对象是蜡块，学生观察到的蜡块运动是合运动。实验可分几步进行。

①将玻璃管倒置并保持竖直不动，看到蜡块沿玻璃管匀速上升。

②让竖直、倒置的玻璃管水平匀速运动（蜡块始终在顶部），观察蜡块的运动。

③观察玻璃管水平匀速运动时蜡块在玻璃管内的运动。

考虑到学生观察时注意力只能集中在某一处，而分析合运动与分运动的关系时需要不断变换观察的对象，可以用视频截图的方式展示动态过程。

教学片段

探究合运动的性质和轨迹

用运动合成演示仪演示笔尖的运动，如图 5–14 所示。

问题 1．如果保持笔尖在水平和竖直方向的运动都是匀速运动，猜想轨迹的形状。图 5–14 甲所示的轨迹与你的猜想一致吗？你能对此进行解释吗？

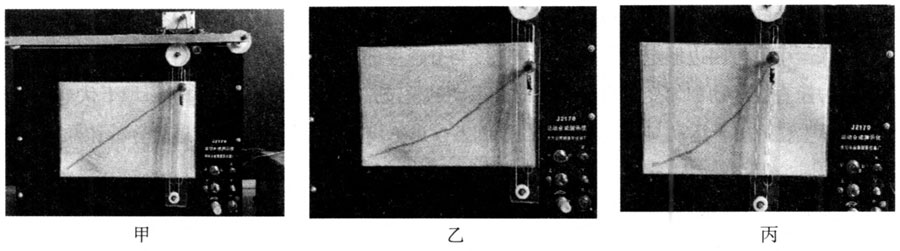
问题 2．如果保持笔尖在水平方向的运动是匀速运动，通过改变电动机的转速使笔尖竖直方向的速度在运动过程中突然变大，试猜想轨迹的形状。图 5–14 乙所示的轨迹与你的猜想一致吗？你能对此进行解释吗？

问题 3．如果保持笔尖在水平方向的运动是匀速运动，笔尖竖直方向的速度在运动过程中均匀增大，试猜想轨迹的形状。图 5–14 丙所示的轨迹与你的猜想一致吗？你能对此进行解释吗？

问题 4．两个互相垂直的直线运动的合运动一定是直线运动吗？

---

上述研究可分成三种情况进行。保持一个方向的运动为匀速运动，另一个方向的运动分别为匀速运动、分两段的匀速运动和速度逐渐变化的运动。第一种情况与教材介绍的蜡块运动相似，可以借此帮助学生了解实验装置，为分析第二种情况打好基础。第二种情况是承前启后的。第三种情况可以在第二种情况的基础上，采用分割成多段的方法进行定性分析。最后在定性分析的基础上，写出轨迹方程，验证定性分析。

通过运动合成演示仪可以画出笔尖运动的三种轨迹（直线、折线和曲线）。运动合成演示仪的原实验装置中只有竖直方向电机可以调速，水平、竖直两个电机共用一个电源，速度可以连续变化的时间很短，这样就导致画出的曲线效果不埋想，因此要把实验装置稍加改进。将水平电机和竖直电机分别接两个独立的学生电源后，在转动竖直方向速度调节旋钮时不断改变两个电机所接电源的电压，这样就可以画出连续的曲线运动轨迹了。

（2）运动的合成与分解

通过运动的分解来研究复杂运动是高中物理中重要的思想方法，也是本节的重点和难点。教学中应避免直接讲解这一方法，可以适当增加一些体验，为学生提供更多生活情景，如商场里自动扶梯正常运行时，在其上面行走的顾客的运动；节日里盛大的焰火表演时，某个火点的运动；田径场上投出的标枪的运动，等等。通过这些情景分析，可以让学生经历运动合成与分解思想的建立过程，体会用运动合成与分解的方法处理问题的等效性。

本节最后安排了“思考与讨论”的问题：如果将玻璃管紧贴着黑板沿水平方向向右匀加速移动，若玻璃管内壁是光滑的，蜡块的轨迹还是一条直线吗？对这一问题的思考，将把前面所学内容延伸到下一节所要研究的问题，起到承上启下的作用。

3．“练习与应用”参考答案与提示

本节配置了 5 道习题，分别以炮弹、跳伞运动员、炮弹、蜡块、汽艇的实际运动为载体，练习在不同的的问题情境中建构物理模型，深化对运动的合成与分解的理解和认识。前 3 题主要让学生熟练运用平行四边形定则定量分析合速度与分速度的关系。第 4 题用作图法让学生体会互成直角的匀速直线运动和匀变速直线运动的合运动的轨迹是曲线，为下一节的学习埋下伏笔。第 5 题是让学生在理解合运动与分运动关系的基础上，进一步对常见的物理现象进行分析和推理，获得结论。

1．如图所示。

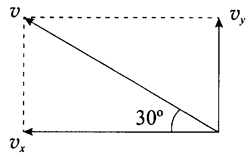
v_x = vcos30° = 800×$\frac{\sqrt{3}}{2}$ m/s = 400$\sqrt{3}$ m/s（693 m/s），v_y = vsin30° = 800× $\frac{1}{2}$ m/s = 400 m/s。

 

2．根据题意，无风时跳伞员着地的速度为 v₁，风的作用使他获得水平速度 v₂，落地速度为 v₁、v₂ 的合速度 v，如图所示。v = $\sqrt{v_1^2+v_2^2}$ = $\sqrt{5^2+4^2}$ m/s = 6.4 m/s。

设速度方向与竖直方向的夹角为 θ，则 tanθ = 0.8，θ = 38.7°。

 

3．炮弹的实际速度方向指向北岸的目标方向，该速度 v 是船的速度 v₁ 与射击速度 v₂ 的合速度，根据平行四边形定则可知，射击的方向偏向目标的西侧。俯视图如图所示。

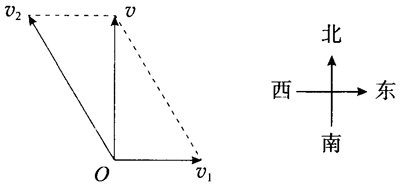
提示：以炮弹发射为素材，理解什么是合运动，什么是分运动，练习用平行四边形定则分析合运动与分运动的关泵。炮弹的实际速度方向为射击速度与船的速度的合速度的方向。

 

4．如图所示。

提示：根据蜡块 1 s 内的水平位移和竖直位移，在坐标纸上描点（4，10）、（16，20）、（36，30）、（64，40），用平滑曲线描绘蜡块的轨迹。

 

5．100 s；100 s；100 m

提示：无论河水是否流动，汽艇驶到对岸的时间都是 t = $\frac{d}{v_1}$ = $\frac{500}{\frac{18}{3.6}}$ s = 100 s。

由于河水流动，汽艇同时被河水冲向下游，沿河运动的速度跟河水流动的速度相同。汽艇沿河水流动方向的位移 l = v₂t = $\frac{3.6}{3.6}$×100 m = 100 m。

即汽艇在对岸下游 100 m 处靠岸。