第四章 第 2 节 全反射
水中的气泡看上去特别明亮,这是为什么呢?

对于折射率不同的两种介质,我们把折射率较小的称为光疏介质(optically thinner medium),折射率较大的称为光密介质(optically denser medium)。光疏介质与光密介质是相对的,例如水、水晶和金刚石三种物质相比较,水晶对水来说是光密介质,对金刚石来说则是光疏介质。根据折射定律,光由光疏介质射入光密介质(例如由空气射入水)时,折射角小于入射角;光由光密介质射入光疏介质(例如由水射入空气)时,折射角大于入射角。
光由光密介质进入光疏介质时,如果入射角不断增大,使折射角增大到 90º 时,会出现什么现象?
观察全反射现象
如图 4.2–1,让光沿着半圆形玻璃砖的半径射到它的平直的边上,在这个边与空气的界面上会发生反射和折射。逐渐增大入射角,观察反射光线和折射光线的变化。
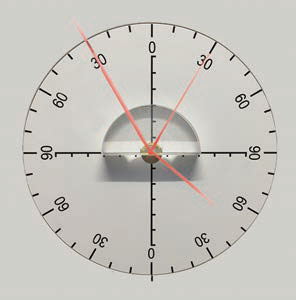

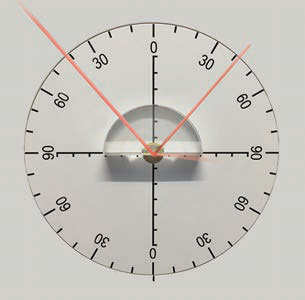
当光从光密介质射入光疏介质时,同时发生折射和反射。如果入射角逐渐增大,折射光离法线会越来越远,而且越来越弱,反射光却越来越强。当入射角增大到某一角度,使折射角达到 90° 时,折射光完全消失,只剩下反射光,这种现象叫作全反射(total reflection),这时的入射角叫作临界角(critical angle)。
当光从光密介质射入光疏介质时,如果入射角等于或大于临界角,就会发生全反射现象。

由于不同介质的折射率不同,在光从介质射入空气(真空)时,发生全反射的临界角是不一样的。怎样计算光从折射率为 n 的某种介质射入空气(真空)发生全反射时的临界角 C?
计算时可以先考虑图 4.2–2 的情形:光以接近 90° 的入射角从空气射入介质,求出这时的折射角。根据光路可逆的道理,也就知道光从介质射入空气时发生全反射的临界角了。
光从介质射入空气(真空)时,发生全反射的临界角 C 与介质的折射率 n 的关系是
\[\sin C = \dfrac{1}{n}\]
从这个关系式可以看出,介质的折射率越大,发生全反射的临界角越小。水的临界角为 48.8°,各种玻璃的临界角为 32° 42°,金刚石的临界角为 24.4°。
科研和技术中常常通过测量临界角来测定材料的折射率。
全反射是自然界中常见的现象。例如,水中或玻璃中的气泡,看起来特别明亮,就是因为光从水或玻璃射向气泡时,一部分光在界面上发生了全反射的缘故。
【例题】
在潜水员看来,岸上的所有景物都出现在一个倒立的圆锥里,为什么?这个圆锥的顶角是多大?
分析 如图 4.2–3,岸上所有景物发出的光,射向水面时入射角 θ1 分布在 0° 到 90° 之间,射入水中后的折射角 θ2 都在 0° 至临界角 C 之间。
解 几乎贴着水面射入水里的光线,在潜水员看来是从折射角为 C 的方向射来的,水面上其他方向射来的光线,折射角都小于 C。因此他认为水面以上所有的景物都出现在顶角为 2C 的圆锥里。
由公式 sin C = \(\dfrac{1}{n}\) 和水的折射率 n = 1.33,可求得临界角

C = arcsin \(\dfrac{1}{1.33}\) = 48.8°
设圆锥的顶角为 α,则有
α = 2C = 97.6°
即圆锥的顶角为 97.6°。
如图 4.2–4,玻璃棱镜的截面为等腰直角三角形,当光从图中所示的方向射入玻璃时,由于光的方向与玻璃面垂直,光线不发生偏折。但在玻璃内部,光射向玻璃与空气的界面时,入射角大于临界角,发生全反射。与平面镜相比,它的反射率高,几乎可达 100%。这种棱镜在光学仪器中可用来改变光的方向,应用十分广泛,例如图 4.2–5 所示的双筒望远镜中的全反射棱镜等。




观察光在弯曲的有机玻璃棒中传播的路径
如图 4.2–6,激光笔发出的光射入一根弯曲的有机玻璃棒的一端,观察光传播的路径有什么特点。
当光在有机玻璃棒内传播时,如果从有机玻璃射向空气的入射角大于临界角,光会发生全反射,于是光在有机玻璃棒内沿着锯齿形路线传播。这就是光导纤维(optical fiber)导光的原理。①
实用光导纤维的直径只有几微米到一百微米。因为很细,一定程度上可以弯折。它由内芯和外套两层组成,内芯的折射率比外套的大,光传播时在内芯与外套的界面上发生全反射(图 4.2–7)。
如果把光导纤维聚集成束,使纤维在两端排列的相对位置一样,图像就可以从一端传到另一端(图 4.2–8)。医学上用这种光纤制成内窥镜②(图 4.2–9),用来检查人体胃、肠、气管等脏器的内部。 实际的内窥镜装有两组光纤,一组把光传送到人体内部进行照明,另一组把体内的图像传出供医生观察。
光也可以像无线电波那样,作为载体来传递信息。载有声音、图像以及各种数字信号的激光从光纤的一端输入,就可以传到千里以外的另一端,实现光纤通信。
光纤通信有传输容量大的特点。例如,一路光纤的传输能力的理论值为二十亿路电话,一千万路电视。此外,光纤传输还有衰减小、抗干扰性及保密性强等多方面的优点。
① 本书用全反射的知识解释了光在有机玻璃棒中的传播,并且由此粗浅地说明了光纤导光的原理。实际上两者并不完全一样。
② 这里介绍的是纤维式内窥镜。现在医院用的大多是电子式内窥镜:把微型摄像头送入人体,图像信号经过电缆传出,用计算机屏幕显示。电子式内窥镜的探头体积小、分辨率高,可供多人观察,所得图像能以电子文件的形式存储。



尽管光纤通信的发展历史较短,但是发展速度惊人。我国的光纤通信起步较早,现已成为技术先进的几个国家之一,目前已经建立了纵横城市之间的光缆通信网络,而且与邻国建立了海底光缆。随着技术的发展,光纤宽带也越来越普及,已有许多企业、家庭实现了光纤入户。光缆线路已经与通信卫星、微波接力站、普通电缆相结合,构成了现代国家的“神经系统”。

水流导光
将塑料瓶下侧开一个小孔,瓶中灌入清水,水就从小孔流出。用激光水平射向塑料瓶小孔(图 4.2–10,激光可由激光笔产生),观察光的传播路径。
1.光由折射率为 1.5 的玻璃和 2.42 的金刚石进入空气时的临界角各是多大?
2.光从折射率为 \(\sqrt 2 \) 的介质中以 40° 的入射角射到介质与空气的界面上时,能发生全反射吗?
3.图 4.2–11 是一个用折射率 n = 2.4 的透明介质做成的四棱柱的横截面图,其中∠ A = ∠ C = 90°,∠ B = 60°,现有一束光从图示的位置垂直入射到棱镜的 AB 面上,画出光路图,确定射出光线。注意:每个面的反射光线和折射光线都不能忽略。
4.图 4.2–12 为光导纤维(可简化为长玻


璃丝)的示意图,玻璃丝长为 l,折射率为 n(n < \(\sqrt 2 \)),AB 代表端面。为使光能从玻璃丝的 AB 端面传播到另一端面,求光在端面 AB 上的入射角应满足的条件。
第 2 节 全反射 教学建议
1.教学目标
(1)知道光密介质和光疏介质的概念,认识光的全反射现象。
(2)知道全反射棱镜及其应用。
(3)初步了解光导纤维的工作原理及光纤技术对社会经济生活的重大影响。
2.教材分析和教学建议
全反射现象在日常生活中经常能遇到,本节要探讨光发生全反射的条件以及相关应用。全反射及其发生的条件是本节的重点,也是培养学生科学思维,帮助他们形成物理观念的重要载体。
教材首先通过展示水中气泡看上去特别明亮的现象引出全反射的话题,意在培养学生通过观察生活现象提出物理问题的科学探究素养。教材介绍光密介质和光疏介质的定义及其相对性,目的是为得出全反射产生的条件作铺垫。教材通过半圆形玻璃砖的演示实验引出全反射的定义和临界角的概念。在演示实验时,要引导学生全面、全程观察。特别要注意观察:随着入射角逐渐增大,反射光线和折射光线的角度和亮度发生变化;当入射角达到某一极限角度时,折射角达到 90°,折射光完伞消失,只剩下反射光。全反射棱镜和光导纤维是对全反射原理的应用,这部分内容有利于开阔学生视野,加深对全反射的认识。
(1)问题引入
本节以“水中的气泡看上去特别明亮,这是为什么呢?”作为新课的引入,老师们可以从日常现象,如熏黑的白炽灯泡放在水中特别明亮,引领学生从生活现象中提出可探究的物理问题。在教师的引导下,学生可能会提出多个问题,如为什么会发生这样的现象?这个现象发生的条件是什么?这个现象的原理是什么?
教学片段
根据实验情境,请同学们思考以下问题。
问题 1.水中的气泡为什么特别明亮?
问题 2.你有怎样的猜想?用怎样的方法才容易说清楚上述问题?
问题 3.如果是玻璃弹子放在水中,弹子会显得特别明亮吗?
问题 4.你对显得特别明亮的条件有何猜想?如何证明你的猜想?
(2)全反射
在“问题引入”的教学中,学生充分体验了全反射现象后,教师要向学生指出,为了更好地表达物理现象和物理规律,首先要学习一些基本概念,引导学生建立光密介质和光疏介质的概念。正确理解光密和光疏的概念,不但要认识“密”与“疏”是相对而言的,还要知道不能把光密、光疏和介质密度的大小混同。例如,酒精对水来说是光密介质,它的密度却比水小。
接着要求学生观察演示实验(或分组进行实验探究),引导学生归纳出发生全反射的两个条件:光从光密介质射入光疏介质以及入射角大于或等于临界角。借助光路图可以帮助学生构建起光的反射、折射和全反射之间的关系,从而理解全反射的主要特征。在实验时,光源最好用氦氖激光光源,而且要在暗室进行或拉上教室四周的窗帘。为了让入射光经过圆心,可以把氦氖激光光源固定在支架上,让支架转动,玻璃砖固定在带有刻度的圆盘的圆心上,以便观察入射角的变化对反射光和折射光的影响。做演示实验时,要使学生看到光从光密介质射入光疏介质时,折射角大于入射角。随着入射角的增大,折射角也逐渐增大,同时折射光逐渐减弱。当入射角达到某一角度时,折射光消失了。再增大入射角,只有反射光,没有折射光。通过对现象的观察,使学生了解全反射现象是光由光密介质射入光疏介质时,入射角达到某一特定值以后产生的现象。这有助于使学生弄清楚临界角的含义。
不同的介质,由于折射率不同,光在射入空气时发生全反射的临界角是不一样的。介质的折射率越大,发生全反射的临界角越小。启发学生用光路可逆的思想,由全反射及折射率的定义来计算某种介质在空气中发生全反射时的临界角。可以引导学生自己计算几种介质的临界角并分析临界角的大小与 n 的关系。对于公式 sinC = \(\dfrac{1}{n}\),要求学生在理解的基础上会灵活应用。
全反射现象在日常生活中比较常见,可以从中选择一些作为演示实验。例如,将空试管斜放在水槽中,然后从其正上方观察试管壁,将会发现试管壁是银白色的。一定要强调发生全反射的条件有两个,但学生常常只记住了判断入射角是否等于或大于临界角,却遗忘了首先应满足光从光密介质射入光疏介质的条件。
在讲解例题的基础上.教师也可以让学生回忆一下在游泳(戴有防水镜)时,从水下观察水上景物的情景。有的学生也许并未体验过,这正激发了他们的好奇心。
(3)全反射棱镜和光导纤维
全反射棱镜和光导纤维是对光的全反射原理的典型应用,特别是后者。教学中一要让学生认真观察光导纤维传输图像的特点,二要分析光导纤维的结构,理解产生全反射的原因。可以利用“演示”栏目中有机玻璃棒导光实验来模拟光导纤维的传输原理。
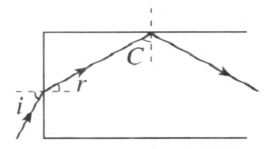
若光导纤维的折射率为 n,在端面上入射光满足什么条件,才能使光在光导纤维中不断发生全反射,从一端传到另一端?
设当光线入射角为 i 时,进入端面的折射光线传到侧面时恰好发生全反射,如图 4–4 所示,则有 sin C = \(\dfrac{1}{n}\),n = \(\dfrac{{\sin i}}{{\sin r}}\),C + r = 90°。解以上各式得 sin i = \(\sqrt {{ n^2} - 1} \),i = arcsin\(\sqrt {{n^2} - 1} \)。可见 i 只要不大于 arcsin\(\sqrt {{n^2} - 1} \),光线就能连续不断地发生全反射,从光导纤维的一端传到另一端。实际上光导纤维外包有外皮层,考虑到外皮层折射率比真空的折射率大,实际入射角比前面计算出的 i 要小。
除了教材中的小实验外,也可做以下实验。在一个盛满清水的烧杯内放两根小试管,甲管内装满清水,乙管内是空气。请同学们观察,哪一根试管特别明亮?为什么?分析总结:观察到乙试管特别明亮,因为光从水射向试管内的空气时,在乙试管表面发生了全反射现象,大量的反射光进入观察者眼中,看起来就显得特别明亮。
3.“练习与应用”参考答案与提示
本节共 4 道习题。第 1 题要求计算临界角,直接应用全反射公式即可;第 2 题和第 3 题根据折射率削断能否发生全反射,并且第 3 题要求根据平面几何知识作出光路图;第 4 题为判断光导纤维发生全反射的条件。
1.41°49′,24°24′
2.不能发生全反射。
3.光路如图 4–5 所示。

提示:光线从左侧垂直 AB 射入棱镜时,透射方向不变。光线射到 CD 时,由几何知识得入射角 i = 30°。该棱镜的临界角为 C,则 sin C = \(\dfrac{1}{2.4}\) < \(\dfrac{1}{2}\),故有 C < 30°,所以光线在 CD 面上发生了全反射。
光线射到 AB 面上时入射角 i′ = 60°,发生全反射,反射光线与 BC 面垂直。
4.设当入射光线入射角为 i 时,进入端面的折射光线传到侧面时恰好发生全反射,如图 4–6 所示,则有 sin C = \(\dfrac{1}{n}\),n = \(\dfrac{\sin i}{\sin r}\),C + r = 90°。解以上各式的 sin i = \(\sqrt {{n^2} - 1} \),i = arcsin \(\sqrt {{n^2} - 1} \)。由于 n < \(\sqrt 2 \),所以 i < arcsin \(\sqrt {2 - 1} \),即 i < 90° 时光线就能传到另一端。

提示:实际上光导纤维外包有外皮层,考虑到外皮层折射率比真空的折射率大,实际入射角比前面计算出的 i 要小。
发布时间:2022/7/12 下午10:14:41 阅读次数:10959
