第 6 节  反冲现象 火箭  教学建议

1．教学目标

（1）通过实验认识反冲运动，能举出反冲运动的实例，知道火箭的发射是反冲现象。

（2）能结合功量守恒定律对常见的反冲现象作出解释。

（3）了解我国航天事业的巨大成就，增强对我国科学技术发展的自信。

2．教材分析与教学建议

本节通过生产生活中的现象介绍反冲运动，通过演示实验加深学生对反冲现象的认识和理解，最后介绍火箭的飞行原理，体现了物理与生活和科技的紧密联系。通过本节的学习，促进学生运动与相互作用观的进一步发展，学会定性分析生产生活中的实际问题。依据教材“思考与讨论”栏目的设计，引导学生根据动量守恒定律，完成对人的速度变化量的推导。在此基础上定量分析火箭的速度。教材在“科学漫步”中介绍“三级火箭”的内容，既是对火箭知识的拓展，又进一步介绍我国在航天事业中的成就，有利于激发学生的爱国热情。

（1）问题引入

教材一开始就提出章鱼、乌贼如何游动的问题，以引发学生的兴趣和思考，使学生认识到反冲现象的普遍性。教师可以播放章鱼、乌贼游动的视频，让学生在仔细观察中发现这类运动的特点。教材中“章鱼游动时体现了什么物理原理？”这一问题，有利于学生将真实物体和运动过程模型化。

（2）反冲现象

首先让学生根据生活经验举出其他反冲运动的例子，认识该类运动的普遍性。做好反冲演示实验是教学中的重要环节，让学生在观察演示实验时思考：物体可看作由哪两部分组成？这两部分构成的系统所受的外力是否近似为 0？或者某一方向上的合力是否近似为 0？让学生理解反冲运动遵循的规律：反冲运动是系统内力作用的结果，当内力远远大于外力时，系统动量近似守恒。解决该类问题时，要选取同一个惯性参考系。

 

教学片段

反冲现象

下面请观察并思考反冲运动实验。

实验 1：把一根弹簧安装在小车上，按动开关之后压缩的弹簧可以分别将几个质量不等的小木块弹出，观察地面上小车的运动。

实验 2：把气球安装在小车上，通过气孔对气球吹气，然后放开气孔，观察地面上小车的运动。

问题 1．以上两个实验，研究的对象分别是什么？试分析受力情况。

问题 2．关于“实验 1”，对比第 4 节实验“参考案例 1”的第 3 种碰撞方式（教材图 1.4–4），两者受力及运动情况是否相似？满足什么规律？类似实例还有哪些？

问题 3．“实验 2”中为什么小车会向前运动？如果让气孔竖直向下排气，你设想会发生什么现象？在航天事业中有类似的应用吗？

问题 4．以上实验中，参考系分别是什么？在匀速运动的火车车厢里能完成吗？

---

从实验中概括反冲运动的特点，运用动量守恒定律，结合生活实际分析运动现象，进一步提升运动与相互作用观。注意动量和速度均是矢量，在不同的惯性参考系中，其数值和方向可以不同，但都满足动量守恒定律。还可以分析反冲时能量的转移和转化，为分析火箭原理进行铺垫。

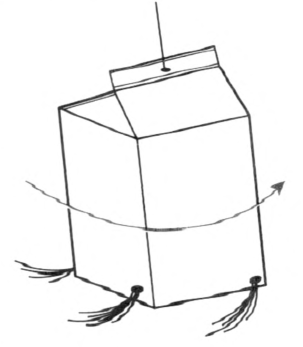
如果没有器材，“做一做”栏目中的第二个实验（教材图 1.6–2 乙）也可以改成“观察从牛奶盒中喷出的水流和纸盒的旋转”实验（图 1–5）。这两个实验涉及力矩和转动，解释时需要分两步走，水喷出时提供一个反作用力，根据初中知识或生活经验，两个方向相反又不在同一直线上的力可以使物体转动。

 

图 1–5

（3）火箭

教材从我国古代火箭讲到喷气式飞机和现代火箭的飞行，都体现了反冲原理的应用。对学生来说，在小学时接触过水火箭，因此对火箭并不陌生，但是对其工作原理并没有研究过。在学习火箭时可以播放水火箭的录像，为讨论火箭提供一个初步的模型。接下来利用“思考与讨论”推进问题，收集和选择有用信息，明确人和小物体是一个系统，以飞船为参考系，根据动量守恒定律进行推导，培养学生准确表述问题、解决问题的能力。

最后，介绍火箭的工作原理，借助前面由动量守恒定律推导出 Δv = − u 的结论，提出问题：火箭如何获得巨大速度？与什么因素有关？对火箭的工作原理进行解释。教学时结合“科学漫步”中的素材，指出由于技术原因，喷气速度存在极限值，引导学生从减轻火箭本身质量下功夫，而火箭结构的强度与质量有关，一步一步引入多级火箭的概念，介绍现代火箭技术。

 

教学片段

火箭

问题情境：设火箭飞行时在极短时间 Δt 内喷射的燃气质量为 Δm，喷出燃气后的火箭箭体质量是 m。研究喷出燃气后，火箭速度是多少。

问题 1．极短时间 Δt 怎么理解？火箭飞行时满足什么规律？以地面与以喷气前的火箭为参考系，结果是否不同？

问题 2．Δv 计算式中的“是喷出的燃气相对喷气前火箭的速度。如果“是喷出的燃气相对地面的速度，结果又有什么区别？

问题 3．如果喷出的燃气相对地面速度均为 u，那么一次相对地面喷出 nΔm 的燃料与分 n 次、每次喷出 Δm 的燃料，结果是一样的吗？如果是相对喷气前的火箭呢？

问题 4．如果火箭是二级火箭，第一次喷射  的燃料后，可抛弃第一级火箭 ，当第二次喷射 的燃料后，火箭速度是多少？（设喷出的燃气相对地面速度均为 u）

---

通过以上的问题，旨在帮助学生理解火箭的飞行原理，理论计算表明：火箭获得的最终速度主要取决于两个条件，一个是喷气速度，另一个是质量比（火箭起飞时的质量与燃料烧尽时的质量之比）。举例说明，单级火箭质量为 2 t．其中推进剂质量为 1.5 t，质量比为 4；如果是二级火箭（各级质量为 1 t，各级内燃料为 0.75 t），第一级火箭推进剂燃烧后被抛弃，剩下的火箭质量比是 8，可见多级火箭有利于提高火箭的最终速度，不过级数太多，每级之间的连接和分离机构也要增多，影响整体的最终速度。

在介绍了火箭的原理、结构之后，再介绍我国在航天事业的成就，激发学生的学习热情和民族自豪感。

3．“练习与应用”参考答案与提示

本节共设置了 4 道习题。第 1 题强调在应用动量守恒定律解题时，各个物体的速度必须相对同一惯性参考系。第 2 题创设科学探索情境。第 3 题以火箭发射人造地球卫星为素材，不但涉及反冲规律，还考查了曲线运动。第 4 题涉及多个物体组成的系统和多个作用过程，体现了动量守恒定律在解决这类问题中的优越性，同时也考查了动量定理。

 

1．飞机的速度还会增加。原因见“提示”。

提示：设飞机的质量为 m₁，喷出气体的质量为 m。以地面为参考系，选取飞机喷气前速度 v₀ 的方向为正方向，喷出的气体的速度为 v₁，飞机喷气后的速度为 v₂，v₁ 的方向与 v₀ 相同，但 v₀ > v₁，由动量守恒定律有（m₁ + m）v₀ = mv₁ + m₁v₂，解得 v₂ = v₀ + 。由于 v₀ > 0，v₁ > 0，且 v₀ > v₁，故有 v₂ > v₀，因此飞机的速度还会增加。

 

2．0.15 kg

提示：喷气后，航天员做匀速直线运动，速度为 v₁ = = 0.075 m/s。设喷气前总质量为 m₁，喷气过程喷出的气体的质量为 m₂，取喷气后航天员的速度方向为正方向，由动量守恒定律得 0 =（m₁ – m₂）v₁ + m₂v₂，解得 m₂ = m₁ = 0.15 kg。

 

3．卫星速度增大到 7.3×10³ m/s，火箭壳体速度为 5.5×10³ m/s，分离后的运动情况见“提示”。

提示：设分离前卫星与火箭壳体的速度 v = 7.0×10³ m/s，分离后卫星与火箭壳体相对地面的速度分别为 v₁ 和 v₂，分离时系统在轨道切线方向上动量守恒，有（m₀ + m₂）v = m₀v₁ + mv₂，且卫星与火箭壳体相对速度 u = v₁ – v₂ = 1.8×10³ m/s，解得 v₁ = 7.3×10³ m/s，v₂ = 5.5×10³ m/s。

分离后，v₁ > v，卫星将做离心运动；火箭壳体分离后的速度 v₂ < v，因此做向心运动，若进入大气层，它的轨道将不断降低，最后将会在大气层中烧毁。

 

4.（1）Δv = \(\frac{8}{{120.01 - 0.01n}}\) m/s

（2）v₁₀ = 0.67 m/s

（3）40 N

提示：设皮划艇、枪（含子弹）及人构成的系统的质量为 m，每发子弹的质量为 m₀，子弹射出的反方向为正方向，子弹相对步枪的速度大小为 u。

（1）设第 1 次射出后艇的速度大小为 v₁，由动量守恒定律得到 0 =（m – m₀）v₁ + m₀（v₁ − u），解得 v₁ = u；设第 2 次射出后艇的速度大小为 v₂，由动量守恒定律得到（m – m₀）v₁ =（m – 2m₀）v₂ + m₀（v₂ − u），解得 v₂ − v₁ = ；设第 3 次射出后艇的速度大小为 v₃，由动量（m – 2m₀）v₂ =（m – 3m₀）v₃ + m₀（v₃ − u），解得 v₃ – v₂ = ……若第 10 次射出后艇的速度大小为 v₁₀，由动量守恒定律应得到（m – 9m₀）v₉ =（m – 10m₀）v₁₀ + m₀（v₁₀ − u），解得 v₁₀ – v₉ = 。通过归纳得出，射出子弹 n 发，每次射击后皮划艇速度的改变量 Δv = = m/s。

（2）连续射击 10 次后，可得 v₁₀ = + + … + = 8×（+ + … + ）m/s = 8×m/s = 0.67 m/s。

（3）设士兵连续射击时间 Δt = 2 s，对整个过程应用动量定理得到 FΔt =（m − 10m₀）v₁₀ – 0，解得 F = = 40 N。