第一章 第 2 节 动量定理
问题？
有些船和码头常悬挂一些老旧轮胎，主要的用途是减轻船舶靠岸时码头与船体的撞击。其中有怎样的道理呢？
两个物体碰撞时，彼此间会受到力的作用，那么一个物体动量的变化和它所受的力有怎样的关系呢？
动量定理
为了分析问题的方便，我们先讨论物体受恒力的情况。如图1.2–1，假定一个质量为 m 的物体在光滑的水平面上受到恒力 F 的作用，做匀变速直线运动。在初始时刻，物体的速度为 v，经过一段时间 Δt ，它的速度为 v′，那么，这个物体在这段时间的加速度就是
\[a = \frac{{\Delta v}}{{\Delta t}} = \frac{{v' - v}}{{\Delta t}}\]
根据牛顿第二定律 F = ma，则有
\[F = m\frac{{v' - v}}{{\Delta t}} = \frac{{mv' - mv}}{{\Delta t}} = \frac{{p' - p}}{{\Delta t}}\]
即
\[\tag{1}\label{1}F\Delta t = p' - p\]
由于 Δp = p′ − p，所以（1）式也可以写成 F = \(\frac{{\Delta p}}{{\Delta t}}\)，它表示：物体动量的变化率等于它所受的力。
（1）式的右边是物体在 Δt 这段时间内动量的变化量，左边既与力的大小、方向有关，又与力的作用时间有关。FΔt 这个物理量反映了力的作用对时间的累积效应。物理学中把力与力的作用时间的乘积叫作力的冲量（impulse），用字母 I 表示冲量，则
\[I = F\Delta t\]
冲量的单位是牛秒，符号是 N·s。有了冲量的概念，
（1）式就可以写成
\[\tag{2}\label{2}I = p' - p\]
（1）式也可以写作
\[\tag{3}\label{3}F(t' - t) = mv' - mv\]
（2）式或（3）式表明：物体在一个过程中所受力的冲量等于它在这个过程始末的动量变化量。这个关系叫作动量定理（theorem of momentum）。
这里说的“力的冲量”指的是合力的冲量，或者是各个力的冲量的矢量和。
物体在碰撞过程中受到的作用力往往不是恒力，物体不做匀变速运动。那么，应该怎样处理这样的问题呢？
我们可以把碰撞过程细分为很多短暂过程（图1.2–2），每个短暂过程中物体所受的力没有很大的变化，这样对于每个短暂过程就能够应用（1）式了。把应用于每个短暂过程的关系式相加，就得到整个过程的动量定理。在应用（1）式处理变力问题时，式中的 F 应该理解为变力在作用时间内的平均值。
动量定理的应用
根据动量定理，我们知道：如果物体的动量发生的变化是一定的，那么作用的时间短，物体受的力就大；作用的时间长，物体受的力就小。例如，玻璃杯落在坚硬的地面上会破碎，落在地毯上不会破碎，用动量定理可以很好地解释此现象。从同样的高度落到地面或地毯时，在与地面或地毯的相互作用中，两种情况下动量的变化量相等，地面或地毯对杯子的力的冲量也相等。但是坚硬的地面与杯子的作用时间短，作用力会大些，杯子易破碎；柔软的地毯与杯子的作用时间较长，作用力会小些，玻璃杯不易破碎。易碎物品运输时要用柔软材料包装，跳高时运动员要落在软垫上（图1.2–3），就是这个道理。
在本节“问题”栏目中，船靠岸如果撞到坚硬的物体，相互作用时间很短，作用力就会很大，很危险。如果在船舷和码头悬挂一些具有弹性的物体（如旧轮胎），就可以延长作用时间，以减小船和码头间的作用力。
【例题】
一个质量为 0.18 kg 的垒球，以 25 m/s 的水平速度飞向球棒，被球棒击打后，反向水平飞回，速度的大小为 45 m/s （图 1.2–4）。若球棒与垒球的作用时间为 0.002 s，球棒对垒球的平均作用力是多大？
分析 球棒对垒球的作用力是变力，力的作用时间很短。在这个短时间内，力先是急剧地增大，然后又急剧地减小为 0。在冲击、碰撞这类问题中，相互作用的时间很短，力的变化都具有这个特点。动量定理适用于变力作用的过程，因此，可以用动量定理计算球棒对垒球的平均作用力。
解 沿垒球飞向球棒时的方向建立坐标轴，垒球的初动量为
p = mv = 0.18×25 kg·m/s = 4.5 kg·m/s
垒球的末动量为
p′= mv′ =－ 0.18×45 kg·m/s =－ 8.1 kg·m/s
由动量定理知垒球所受的平均作用力为
\[F = \frac{{p' - p}}{{\Delta t}} = \frac{{ - 8.1 - 4.5}}{{0.002}}\;{\rm{N}} = - 6\;300\;{\rm{N}}\]
垒球所受的平均作用力的大小为 6 300 N，负号表示力的方向与坐标轴的方向相反，即力的方向与垒球飞来的方向相反。
科学漫步
历史上关于运动量度的争论
历史上，一种观点认为应该用物理量 mv 来量度运动的“强弱”；另一种观点认为应该用物理量 mv2 来量度运动的“强弱”。主张以 mv 量度运动的代表人物是笛卡儿。他认为：“在物质中存在一定量的运动，它的总和在世界上永远不会增加也不会消失。”这实际上是后来所说的动量守恒定律的雏形。主张以 mv2 量度运动的代表人物是莱布尼兹。他认为守恒的应该是 ∑mv2 而不是 ∑mv 。经过半个多世纪的争论，法国科学家达兰贝尔用他的研究指出，双方实际是从不同的角度量度运动。
用现在的科学术语说，就是：“力”既可以通过动量来表示
\[F = \frac{{\Delta p}}{{\Delta t}}\]
又可以通过动能来表示
\[F = \frac{{\Delta {E_{\rm{k}}}}}{{\Delta x}}\]
动量决定了物体在力 F 的阻碍下能够运动多长时间，动能则决定了物体在力 F 的阻碍下能够运动多长距离。也就是说，动量定理反映了力对时间的累积效应，动能定理反映了力对空间的累积效应。
这场争论一方面促进了机械能概念及整个能量概念的形成，并使人们对多种运动形式及其相互转变的认识更加深入；另一方面，动量与动量守恒定律也在争论中显示出了它们的重要性。
STSE
汽车碰撞试验
汽车安全性能是当今衡量汽车品质的重要指标。实车碰撞试验是综合评价汽车安全性能最有效的方法，也是各国政府检验汽车安全性能的强制手段之一。
1998 年 6 月 18 日，国产轿车在清华大学汽车工程研究所进行的整车安全性碰撞试验取得成功，被誉为“中国轿车第一撞”。从此，我国汽车的整车安全性碰撞试验开始与国际接轨。
当汽车以 50 km/h 左右的速度撞向刚性壁障时，撞击使汽车的动量瞬间变到 0，产生了极大的冲击力（图 1.2–5）。“轰”的一声巨响之后，载着模拟乘员的崭新轿车眨眼间被撞得短了一大截。技术人员马上查看车辆受损情况：安全气囊是否爆开？安全带是否发挥了作用？前挡风玻璃是否破碎？“乘员”是否完好无损？车门是否能够正常开启？…… 还要取出各种传感器，做进一步处理，通过计算机得到碰撞试验的各项数据。
汽车碰撞时产生的冲击力不仅很大，而且很复杂。在碰撞瞬间冲击力与碰撞的速度、相撞双方的质量分布、接触位置的形状、材料、变形等因素相关。通过“乘员”身上的传感器采集的数据，研究人员可以评估人体相应部位所受冲击力的大小。根据这些结果，汽车厂家可以改进车辆的结构设计，增加乘员保护装置，使我们乘坐的汽车越来越安全。
练习与应用
1．如图 1.2–6，一物体静止在水平地面上，受到与水平方向成 θ 角的恒定拉力 F 作用时间 t 后，物体仍保持静止。现有以下看法：
A．物体所受拉力 F 的冲量方向水平向右
B．物体所受拉力 F 的冲量大小是 Ftcos θ
C．物体所受摩擦力的冲量大小为 0
D．物体所受合力的冲量大小为 0
你认为这些看法正确吗？请简述你的理由。
2．体操运动员在落地时总要屈腿（图1.2–7），这是为什么？
3．如图 1.2–8，用 0.5 kg 的铁锤钉钉子，打击前铁锤的速度为 4 m/s。打击后铁锤的速度变为 0，设打击时间为 0. 01 s。
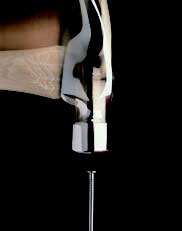
（1）不计铁锤所受的重力，铁锤钉钉子的平均作用力是多大？
（2）考虑铁锤所受的重力，铁锤钉钉子的平均作用力是多大？
（3）你分析一下，在计算铁锤钉钉子的平均作用力时，在什么情况下可以不计铁锤所受的重力。
4．一个质量为 10 kg 的物体，以 10 m/s 的速度做直线运动，受到一个反向的作用力 F，经过 4 s，速度变为反向 2 m/s。这个力是多大？
5．一个质量为 60 kg 的蹦床运动员，从离水平网面 3.2 m 高处自由下落，着网后沿竖直方向蹦回到离水平网面 5.0 m 高处。已知运动员与网接触的时间为 0.8 s，g 取 10 m/s2 。
（1）求运动员与网接触的这段时间内动量的变化量。
（2）求网对运动员的平均作用力大小。
（3）求从自由下落开始到蹦回离水平网面 5.0 m 高处这一过程中运动员所受重力的冲量、弹力的冲量。
6．曾经有一则新闻报道，一名 4 岁儿童从 3 层高的楼房掉下来，被一名见义勇为的青年接住。请你估算一下，儿童受到的合力的冲量是多大？设儿童与青年之间的相互作用时间为 0.1 s，则儿童受到的合力的平均值有多大？
第 2 节 动量定理 教学建议
1．教学目标
（1）能在恒力情况下进行理论推导，得出动量定理及其表达式。
（2）知道冲量概念，知道动量定理及其表达式的物理意义。
（3）知道动量定理适用于变力情况，领会求解变力冲量时的极限思想。
（4）会用动量定理解释生活生产中的相关现象和饵决实际问题。
2．教材分析与教学建议
动量定理是一个重要的规律，它揭示了力在一段时间内连续作用的累积效果与动量变化之间的关系，进一步揭示了运动状态变化与相互作用之间的关系。前一节内容重在建立动量概念，并没有关注一个物体动量变化的原因。通过恒力情况下的理论推导，可以认识到冲量是动量发生变化的原因，同时动量定理也是下一节从理论上推导动量守恒定律的基础。教材虽然是在恒力作用的情况下由牛顿第二定律推导出动量定理的，但是动量定理不仅适用于恒力的情况，也适用于变力的情况。正因为如此，动量定理在实际中有更广泛的应用，尤其在解决作用时间短、作用力大而且随时间变化快的打击、碰撞等问题时，用动量定理要比用牛顿第二定律更方便。
在前面的学习中，学生已经具有力、加速度、动量和牛顿第二定律等知识，掌握了矢量的运算法则，具备一定的分析和推理论证能力，具有通过建立简单的物理模型解决生活中实际问题的能力，但是面对复杂情境，学生还是有较大的困难。本节中动量定理的矢量性，是学生学习的一个难点，需要在解决问题的过程中，通过遵循严格的程序和规范的运算来加以突破。本节课的教学重点是动量定理的推导及应用。
（1）问题引入
教材通过创设“有些船和码头悬挂一些老旧轮胎，主要的用途是减轻船舶靠岸时码头与船体的撞击”的情境，引发学生思考“其中有怎样的道理呢？”生活中常见的类似问题有很多，例如，跳远的时候要跳到沙坑里，跳高时在下落处要放海绵垫，从高处往下跳，落地后双腿往往要弯曲，所有这些行为（或措施）的共性在哪里？在于延长相互作用的时间。而在有些情况下，我们又不希望这样，比如通常用铁锤钉钉子，而不用橡皮锤钉钉子，这又是为什么呢？教师可以创设基于生活的问题情境来引发学生更深入的思考。
（2）动量定理
要注意对力的冲量这个概念的理解，加强对动量矢量性的认识。动量是矢量，它的方向就是速度的方向，冲量也是矢量，但它的方向不能笼统地说是力的方向。只有在作用时间内，力的方向不变时，冲量的方向才是力的方向。冲量是在作用时间内，力对这段时间的累积效应，而不是简单的力和力的作用时间的乘积。如果在作用时间内，力的方向不断改变，冲量的方向可能跟任何时刻力的方向都不相同。
注意动量定理中的冲量是指合外力的冲量。要认识到动量定理和牛顿第二定律的区别：动量定理反映了合力在时间上的累积效果——改变物体的动量，牛顿第二定律反映了合力的瞬时作用效果——使物体产生加速度。
教材在应用牛顿第二定律与运动学公式推导动量定理的过程中，研究对象所受的力是恒力，这样做的目的是简化推导过程，并不代表动量定理只适用于恒力作用的情况。
教学片段
冲量与动量定理
问题 1．怎样应用牛顿第二定律及匀变速直线运动的公式推导恒力与动量变化的关系？
问题 2．F、Δp 和 Δt 间的关系是 F = \(\frac{{\Delta p}}{{\Delta t}}\)，它的物理意义是什么？
问题 3．有了冲量的概念后，F Δt = pʹ − p 就可以简化为 I = Δp，如何理解该式的物理意义？
问题 4．前面的推导是物体在恒力的作用下做匀变速直线运动情况下得出的，实际上物体所受的力往往不是恒力，也不一定做匀变速直线运动，那么动量走理还成立吗？
问题 5．如何理解变力的冲量，教材中利用 F–t 图像求变力冲量的方法（教材图 1.2–2），我们曾经在哪些物理量的求解中用到过？
教材给出的动量定理的表达式是矢量式。在处理一维问题时，需选定一个正方向，简化为代数运算。在动量定理推导中，以初速度的方向为正方向，力及末动量的方向都以初速度的方向为参照，在分析教材例题时要注意明确研究对象（垒球）和初、末速度方向，加深对动量定理矢量性的理解。对于利用 F–t 图像求变力的冲量，可以与已有知识，如利用 v–t 图像求变速直线运动位移、利用 F–x 图像求变力所做的功等进行类比学习。
（3）动量定理的应用
动量定理在工农业生产和日常生活中有广泛的应用。用动量定理来解释生产生活中的现象，应紧扣某一物理过程中物体的动量变化、作用时间以及作用力，可以结合一些演示实验来模拟生活现象并应用动量定理进行分析、解释。
教学片段
用动量定理解释生活现象
播放蹦极的视频。然后用橡皮筋和钩码模拟蹦极过程，再将橡皮筋换成细棉线做实验。
问题 1．蹦极运动中绑在运动员身上的是弹性绳而不是非弹性绳，这样做的主要目的是什么？
问题 2．实验中，钩码先后两次下落，你观察到什么现象？两个钩码的“命运”不同，原因是什么？
问题 3．在动量的变化量 Δp 一定的情况下，F 和 Δt 之间有什么关系？
问题 4．你能否用动量定理解释落在瓷砖上的鸡蛋会破，而落在海绵上的鸡蛋不会破？
问题 5．日常生活中还有哪些现象也可以用动量定理来解释？
在教学过程中，引导学生知道：当 Δp 一定时，Δt 越大 F 越小，Δt 越小 F 越大。教学过程中对“问题5”的回答可以充分展开，学生在日常生活及体育运动中遇到大量与动量定理有关的问题，如运送易碎品要用柔软的包装，跑步时穿减震性能好的跑鞋，接球时有个自然的屈臂回缩过程，等等。
引导学生总结：在碰撞中，我们要得到很大的作用力，就要缩短力的作用时间，而有时需要延长作用时间来减小作用力。
在“科学漫步”栏目中介绍了历史上关于运动量度的争论。一方面，加深对动量概念建立过程的了解。另一方面，通过物理学史认识动量和动能实际上是从不同角度描述物体运动的量。动量决定了物体在力 F 的阻碍下能够运动多长时间，动能则决定了物体在力 F 的阻碍下能够运动多长距离。从这个角度来看，动量定理反映了力对时间的累积效应，动能定理反映了力对空间的累积效应。引导学生推导出物体在某一状态下，其动量大小与动能大小的关系为 p2 = 2mEk 或 Ek = \(\frac{{{p^2}}}{{2m}}\)，加深学生对动量、动能之间联系的认识。
在“STSE”栏目中介绍了汽车碰撞试验。在教学中，可通过对汽车安全带、安全气囊和交通规则的介绍，加强学生安全意识、开阔学生视野、提高学生科学素养，将科学·技术·社会·环境相结合的理念，融入日常的问题解决当中。
3．“练习与应用”参考答案与提示
本节共设置了 6 道习题。第 1 题考查学生对冲量定义的理解。第 2 题让学生运用动量定理解释生活中的现象。第 3、4、5、6 题让学生运用动量定理进行相关计算，其中第 3 题涉及打击过程中物体的重力是否可以忽略不计的问题，第 6 题是源于生活实际的估算题，目的是培养学生的建模能力。
1．D 看法正确
提示：A．物体所受拉力 F 的冲量方向与 F 的方向相同
B．物体所受拉力 F 的冲量大小是 Ft
C．物体所受摩擦力的冲量大小是 Ftcosθ
D．物体所受合力 F 的冲量大小是 0
2．体操运动员在着地时，动量的变化量是一定的，通过屈腿，可以延长运动员与地面间的作用时间，由动量定理可知，将会减少地面对运动员的作用力，从而使运动员避免受伤。
3．（1）200 N；（2）205 N；（3）当打击时间很短时，可以不计铁锤所受的重力。
提示：（1）打击时，铁锤受到重力和钉子对铁锤竖直向上的弹力，打击后铁锤的速度为 0。设竖直向下为正方向。若不计铁锤所受的重力，根据动量定理有 − FΔt = 0 − mv，解得F = 200 N。（2）若考虑铁锤所受的重力，则有（G − F）Δt = 0 − mv，解得 F = 205 N。（3）从前两问的解答可以看出，当打击时间很短时，铁锤所受的重力可以忽略不计。
4．30 N
5．（1）1 080 kg．m/s，方向竖直向上；（2）1 950 N，方向竖直向上；（3）重力的冲量为 1 560 N·s，方向竖直向下；弹力的冲量为1 560 N·s，方向竖直向上。
6．165 N·s：1 650 N
提示：此题为估算题。假设儿童质量 m = 15 kg，每层楼高 3 m，窗台离楼板高 1 m．青年接到儿童时手臂离地面高度也为 1 m，忽略其他情况，选竖直向下为正方向，g 取 10 m/s2。儿童在接触青年手臂前下落的高度 h = 6 m，儿童刚被接住时的速度 v = \(\sqrt {2gh} \) = 11 m/s，根据动量定理，儿童受到的合力的冲量 I = 0 −mv = − 165 N·s，负号表示方向竖直向上。儿童与青年之间的相互作用时间 Δt = 0.1 s，则儿童所受合力的平均值 F = 1 650 N，方向竖直向上。
发布时间：2022/6/30 下午2:48:36 阅读次数：3981
