第十一章 第二节 气体的等温变化
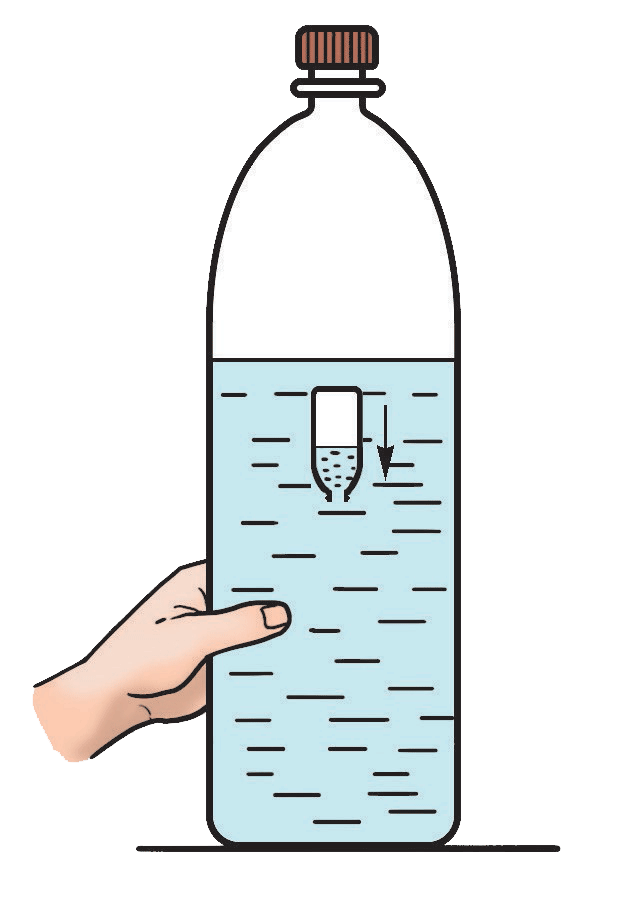
图 11–8 浮沉子
如图 11–8 所示,在一个大塑料瓶里装入大半瓶水,并放入一个倒扣的小瓶,小瓶内留有大约一半水,使其刚好浮出水面。拧紧大瓶的盖子,用力挤压大瓶,就可以看到小瓶下沉。这个装置叫做浮沉子。
用力挤压大瓶时,其上方封闭气体的状态发生变化,最终导致小瓶下沉。在这个过程中,封闭气体的三个状态参量是怎样变化的呢?它们彼此间有什么定量关系吗?
描述气体状态的三个状态参量之间存在一定的关系。本节将通过实验研究一定质量的气体在温度保持不变的情况下气体压强与体积之间的变化关系,这个变化过程叫做等温变化。
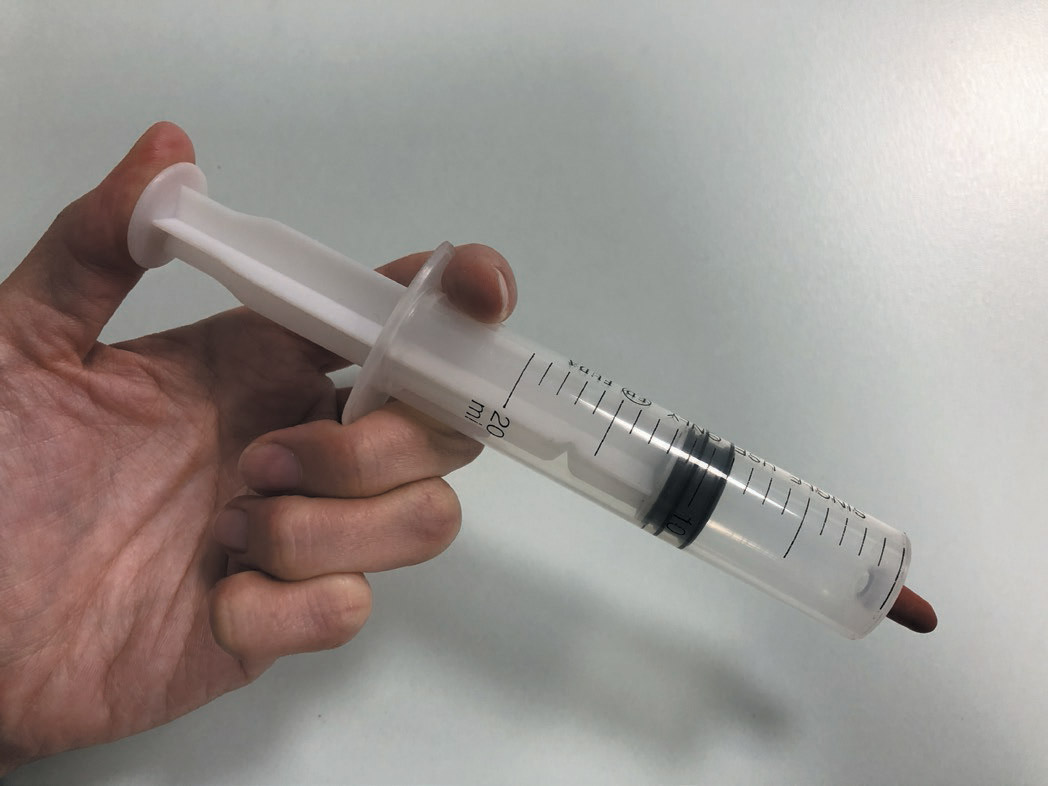
图 11–9 推、拉注射器活塞
如图 11–9 所示,将活塞置于塑料注射器中部,用橡皮帽封住注射口,体会推、拉活塞时的感觉,并观察松手后活塞的运动。
在上述活动中,无论是推还是拉,我们都能感受到阻力,并且活塞移动的距离越大这种阻力越大。根据上述现象,你能对封闭在注射器内气体的压强与体积之间的变化关系提出猜想吗?
探究等温情况下一定质量气体压强与体积的关系
提出问题
注射器内的封闭气体体积减小时压强增大,体积增大时压强减小。等温情况下,一定
质量气体的压强是否与体积成反比?
实验原理与方案
一定质量的气体状态发生变化时,其压强、体积、温度都有可能发生变化。为了研究压强与体积的关系,需要控制气体的温度保持不变。
改变气体体积,测出不同的体积 V 及其对应的压强 p,研究 p 与 V 之间是否存在反比关系。
实验装置与方法
图 11–10 探究等温情况下气体压强与体积的变化关系
如图 11–10 所示的实验装置可供选用。
以注射器内的封闭气体为研究对象,由注射器的刻度读出封闭气体的体积,由压强传感器测量气体的压强;多次改变注射器活塞的位置,获得多组封闭气体的体积和压强的测量值。
本实验采用作图的方法分析数据,得出 p、V 之间的函数关系。
实验操作与数据收集
将注射器与压强传感器的检测口相连,封闭一定质量的气体。缓慢推、拉注射器活塞,在活塞位于各个设定体积所对应的刻度时记录相应的压强测量值并填入表 11–2。
表 11–2 实验数据记录表
|
实验序号 |
1 |
2 |
3 |
4 |
5 |
|
V/mL |
|
|
|
|
|
|
p/Pa |
|
|
|
|
|
数据分析
根据实验数据,选择合适的坐标系描点作图,研究 p 与 V 之间是否存在反比关系。
实验结论
_________________________________________________________________________
_________________________________________________________________________
交流与讨论
(1)在实验中,怎样确保封闭气体的温度不变?
(2)各组得到的 p 与 V 乘积的平均值一致吗?若不一致,分析可能的原因。
英国化学家、物理学家玻意耳(图 11–11)和法国科学家马略特(E. Mariotte,1620—1684)各自通过实验发现,一定质量的气体在温度不变时,压强与体积成反比。这个结论叫做玻意耳定律(Boyle’s law)。

图 11–11 玻意耳(R.Boyle,1627—1691)
图 11–12 等温线
图 11–13
如果用 p1、V1 和 p2、V2 分别表示一定质量的气体在等温变化中任意两个状态的压强、体积,玻意耳定律可表示为
\(\color{#837D23}\frac{{{p_1}}}{{{p_2}}} = \frac{{{V_2}}}{{{V_1}}}\) 或 p1V1 = p2V2
如图 11–12 所示是一定质量的气体经历等温变化时的 p–V 关系曲线,叫做等温线(isotherm)。在 p–V 坐标系中,等温线是一条双曲线。
利用玻意耳定律可以解释图 11–8 中浮沉子的运动。挤压大瓶时,大瓶内水面上方的封闭空气体积减小,压强增大,水被压入小瓶中,使小瓶中水的质量增加,小瓶所受浮力减小,于是小瓶下沉。
示例 一个体积为 V 的气泡自池塘底浮起,如图 11–13 所示。若水深为 3 m,气泡从池底上升到水面时体积将变为原来的多少倍?(设水底和水面温度相同,大气压强 p0 = 1.0×105 Pa,水的密度 ρ = 1.0×103 kg/m)
分析:由于水底和水面温度相同,而且气泡在上升过程中质量没有发生变化,所以遵循玻意耳定律。只要算出气泡在水底和水面时的内部气体压强,即可求出体积的变化情况。
解:在池底时,气泡内部气体压强 p1 = p0 + ρgh,体积 V1 = V;当气泡浮到水面后,气体压强 p2 = p0,体积为 V2。根据玻意耳定律
p1V1 = p2V2
所以, \({V_2} = \frac{{{p_1}{V_1}}}{{{p_2}}} = \frac{{({p_0} + \rho gh)V}}{{{p_0}}}\)
= \(\frac{{(1.0 \times {{10}^5} + 1.0 \times {{10}^3} \times 9.8 \times 3)}}{{1.0 \times {{10}^5}}}V\)
≈ 1.29V
因此,气泡从池底上升到水面时体积将变为原来的 1.29 倍。
在应用玻意耳定律解题时,首先要搞清楚是否满足温度不变和气体质量不变的条件,然后分清两个不同状态的压强和体积值。在运算过程中不一定要用国际单位,只要方程两边使用的单位相同就可以了。
根据玻意耳定律,气体体积被压缩时压强增大,大客车的制动系统和车门开关机构通常就是以压缩空气作为动力来控制的。
图 11–14 所示是位于大客车车门上方的双向气阀构造图。从图中可看出,电磁控制阀的作用是使压缩空气根据需要轮流从进气管进入汽缸内活塞的两侧,使活塞做往复运动,从而实现开门和关门的动作。
图 11–14 大客车双向气阀构造图
玻意耳定律反映了气体宏观状态的变化规律,这一规律可用分子动理论的观点从微观角度加以解释。气体的压强取决于温度和容器内气体的分子数密度。当质量一定的气体温度不变时,气体的压强仅与气体的分子数密度有关。故体积越小,气体分子数密度越大,单位时间内撞击单位面积的分子数越多,气体的压强就越大。
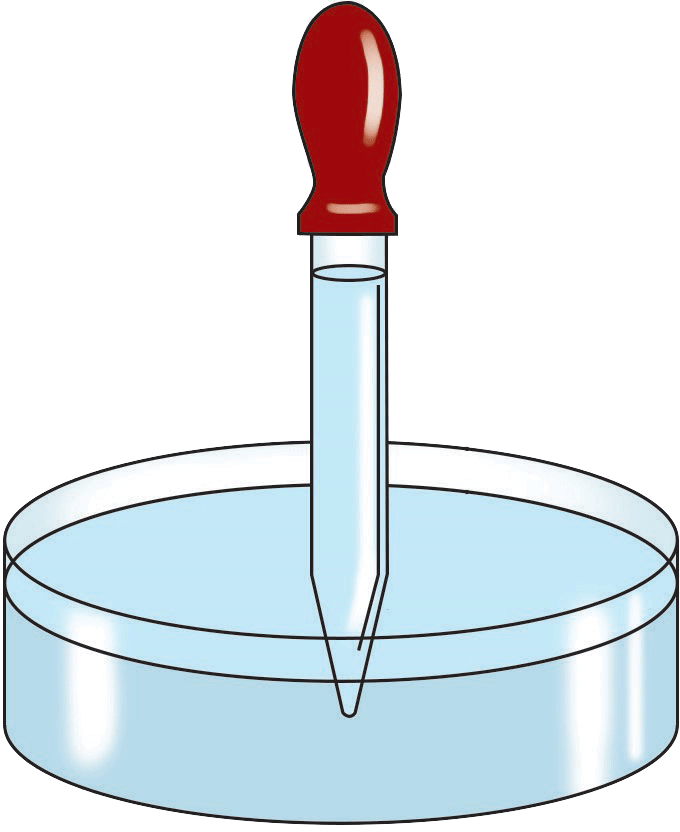
图 11–15
- 在本节的“自主活动”中,推活塞时感觉很费劲,有人说这表明分子间有斥力。请对此作出判断并简述理由。
- 如图 11–15 所示,滴管尾部套有弹性橡胶球。挤压橡胶球,然后把滴管的玻璃嘴放入水中,松手后,水便进入滴管内部。解释上述现象。

图 11–16
- 如图 11–16 所示,在球形瓶中放入一个气球,把气球的开口端翻在球形瓶的瓶口上,然后向气球内吹气,简述将要发生的现象及其原因。
- 湖底腐烂的植物释放出沼气,当遇到严寒天气时沼气泡在水中被冰冻起来,自下而上越来越大,形成一道有趣的风景(图 11–17)。
(1)简述上述现象的成因。
(2)若一个沼气泡从湖底升至湖面时体积加倍,估算湖水的深度。

图 11–17
图 11–18
图 11–19
- 如图 11–18 所示的潜水钟(一种沉放到水下,研究水底情况的装置,也可作为检修大桥桥墩及其他建筑设施水下部分的潜水装置)高 2 m,开口端竖直向下沉到 10 m 深的水底,求进入钟内的水深 h。(设钟内封闭气体的温度保持不变,大气压强 p0 = 1.0×105 Pa,水的密度 ρ = 1.0×103 kg/m3,g 取 10 m/s2)
- 某小组同学应用玻意耳定律设计了一个测量大气压强的实验方案:一端封闭、粗细均匀的玻璃管开口向上竖直放置,内有一段汞柱封闭了一定质量的空气,如图 11–19 所示。多次改变管内汞柱长度,测量多组汞柱的长度 h 和空气柱的长度 l;然后在 h - \(\frac{1}{l}\) 坐标系中描点作图。
(1)写出所作图线的函数表达式。
(2)如何利用该图线求出大气压强?
本节编写思路
本节基于上一节课的学习内容,在用体积、温度、压强描述气体状态的基础上,提出采用控制变量的方法,通过实验手段来研究一定质量的气体等温变化时所遵循的规律。
本节内容主要分为三部分:一是通过实验探究气体等温变化规律,二是玻意耳定律,三是玻意耳定律的微观解释。其中探究实验是重点。
探究实验分为定性与定量两部分。首先在自主活动体验的基础上,对一定质量气体等温过程中压强与体积的关系提出猜想,然后通过学生实验从定量的角度予以验证。
在探究实验中,学生先基于直观感受提出猜想,然后经过收集、分析、处理数据等一系列过程,最终得出结论并相互交流。该实验过程旨在提升科学探究能力,培养严谨的科学态度与实事求是的科学精神。
正文解读
通过“自主活动”,引导学生基于感觉和现象提出猜想,为后续的定量探究实验确立方向。教学中要提示学生,注意体会用手推、拉活塞时手指上不同的感觉,进而说明密闭气体体积大小不同对应的压强不同。明确探究实验的研究对象为封闭在针筒内的气体,探究的是密闭气体状态发生变化时压强随体积变化的规律。
建议在介绍“实验装置与方法”时,组织学生对下列问题展开讨论,确保学生操作正确,有利于实验结论的得出。
实验过程中:
(1)如何确保气体质量一定?
(2)如何控制气体的温度保持不变?
(3)如何确保每次读数时气体处于平衡状态?
利用教材图 11 – 10 所示装置进行实验时,需要注意:在针筒和压强传感器的连接管内有一定气体,因此封闭气体的体积应该等于由针筒刻度读出的体积值与软管容积的和。教学中可以根据学生的水平,选择采取以下两种教学方式:
(1)直接告知学生软管容积的数值,记录的封闭气体体积应该为:针筒刻度读出的体积值 + 软管容积值。
(2)先不告知软管内存在气体这一事实,学生将由针筒刻度读出的体积值当作封闭气体的体积。在用图像处理数据时发现每组作出的 V – \(\frac{1}{p}\) 图线在 V 轴上都有一段截距,再引导学生观察实验装置,寻找问题所在。发现问题之后,再告知软管的容积,请学生重新处理数据,观察图线的变化,最终经分析得出规律。
交流与讨论中的问题(2)的用意:① 多组同学的实验结论都证明:一定质量的气体等温变化时,p 与 V 乘积是个常量,帮助学生明确科学规律是通过大量实验得出来的,是可重复的,不能通过一次实验就轻易下结论;② 发现不同小组的 p 与 V 乘积不同,可帮助学生明确 p 与 V 乘积所对应的常数与封闭气体的质量有关,实验所得的结论是有适用条件的。
在学习玻意耳定律的过程中,可让学生练习用文字叙述、数学表达式和图像三种方式来描述物理规律,从而加深对等温变化过程的理解,为后续学习查理定律和盖·吕萨克定律奠定基础。要帮助学生明确:在 p – V 图线上任意一点与一组(p,V)数据对应,表示一定质量气体的一个状态。
通过此示例帮助学生学会从真实情境中抽象出物理模型——一定质量的气体发生等温变化,进而确定初、末状态的体积和压强,运用玻意耳定律解决基于真实情境所提出的问题。运用气体实验定律解决实际问题的策略与解决力学、电学问题有所不同,教学中要注意示范。
一定质量的气体,其分子总数是一定的。在一定的温度下,气体分子运动的平均速率是不变的,所以压强只与单位体积中的分子数有关。当气体的体积缩小时,单位体积内的分子数增加,在单位时间内分子对单位面积器壁的碰撞次数将增加,所以压强就增大。同理,当体积增大时,单位体积中的分子数减少,压强也减小,所以在温度恒定时,一定质量的气体的压强与体积成反比。
问题与思考解读
1.参考解答:这种说法是错误的。向下推活塞导致气体体积减小,分子间距离减小,但由于物质还是气体状态,分子间距离仍然大到可以忽略分子间的相互作用力。推活塞感觉费劲是因为气体密度增大,单位时间内撞击单位面积器壁的分子数增多,导致气体压强增大。
命题意图:解释宏观现象背后的微观原因,运用理论依据说明自己的观点。
主要素养与水平:科学论证(Ⅱ)。
2.参考解答:把滴管的玻璃嘴放入水中,在橡胶球和滴管内封闭了一定质量的空气。松手后,这部分空气的体积增大,压强减小,因此滴管内外气体存在压强差,这个压强差使水进入滴管内部。
命题意图:运用玻意耳定律解释生活中的现象。
主要素养与水平:科学推理(Ⅱ)。
3.参考解答:用力吹气球,但气球体积略增大后便不再增大。在气球和球形瓶之间封有一定量的空气,当用力向气球内吹气时,这部分密闭气体会被压缩,压强增大,使气球很难被吹大。
命题意图:从真实情境中抽象出研究对象,以定性的角度预测并解释现象。
主要素养与水平:模型建构(Ⅱ);科学论证(Ⅱ)。
4.参考解答:(1)沼气泡在湖底生成时有一定的体积和压强。在上升过程中,温度变化不大;随着深度变浅,气泡内气体的压强越来越小,气泡内外压强差变大,所以体积越来越大。
(2)设大气压强为 p0,沼气泡在湖底压强为 p1、体积为 V1,升至湖面时的压强为 p2、体积为 V2,湖水深度为 h,有 p1 = p0 + ρgh,p2 = p0,V2 = 2V1。根据 p1V1 = p2V2 可得 h ≈ 10 m。
命题意图:应用玻意耳定律,从定性、定量角度解决从实际情境中抽象出的问题,培养物理观念。
主要素养与水平:模型建构(Ⅱ);科学推理(Ⅱ)。
5.参考解答:已知 p1 = p0,p2 = p0 + ρg(10 m − h),V1 = S·2 m,V2 = S(2 m − h)。
根据 p1V1 = p2V2 可解得 h ≈ 0.95 m
命题意图:应用玻意耳定律解决实际问题,培养物理观念。
主要素养与水平:模型建构(Ⅱ);科学推理(Ⅲ)。
6.参考解答:(1)h = \(\frac{c}{{\rho gS}}\)·\(\frac{1}{l}\) − \(\frac{{{p_0}}}{{\rho g}}\)(c 为常数,ρ 为汞的密度,p0 为大气压强,S 为玻璃管横截面积)
(2)图线在纵轴上的截距的绝对值为 \(\frac{{{p_0}}}{{\rho g}}\),由此可求出大气压强。
命题意图:能基于玻意耳定律理解实验原理,解释实验图像的物理意义。
主要素养与水平:科学推理(Ⅱ);解释(Ⅲ)。
发布时间:2022/6/23 下午10:08:58 阅读次数:6570
