第十章 第三节 分子运动速率分布的统计规律
组成物质的大量分子在永不停息地做无规则运动。对单个分子而言,速度方向随机变化,速率时大时小;任意两个分子的运动方向和速率一般不相同。但是,当我们研究大量气体分子时又会发现,大量分子的运动却表现出一定的规律性。
图 10–14 所示的装置称为伽尔顿板,其上部规则地布有许多铁钉,下部用隔板分割成许多等宽的竖直狭槽,大量小球可通过中间漏斗形入口落下,装置前有玻璃板覆盖,使小球最终落在槽内。重复实验多次,发现某个小球落入哪个槽内完全是随机的,但大量小球在槽内的分布却是有规律的,越靠近中间小球越多。
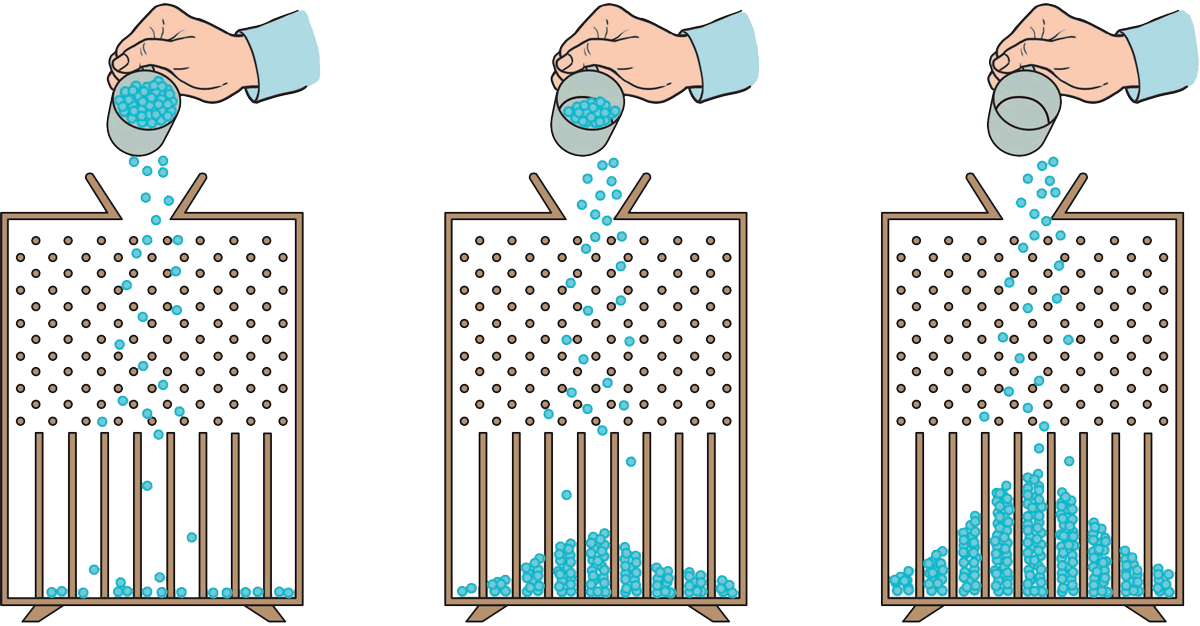
图 10–14 “伽尔顿板”实验
这种大量随机事件的整体表现所显示的规律性叫做统计规律。
“伽尔顿板”实验的结果给我们这样的启示:对于由大量分子组成的系统,个别分子的运动并无规律可言;但大量分子的热运动,却可能显示出一定的统计规律。
对气体的大量实验表明,所有分子速率的分布符合一定的统计规律。
表 10–1 是 0℃ 和 100℃ 时氧分子的速率分布。其中 0℃ 时的氧分子在各速率区间分布的直方图如图 10–15 所示。
表 10–1 0℃ 和 100℃ 时氧分子的速率分布
|
v (/ m·s-1) |
各速率区间的分子数占分子总数的百分率 /% |
|
|---|---|---|
|
0℃ |
100℃ |
|
|
100 以下 |
1.4 |
0.7 |
|
100~200 |
8.1 |
5.4 |
|
200~300 |
17.0 |
11.9 |
|
300~400 |
21.4 |
17.4 |
|
400~500 |
20.4 |
18.6 |
|
500~600 |
15.1 |
16.7 |
|
600~700 |
9.2 |
12.9 |
|
700~800 |
4.5 |
7.9 |
|
800~900 |
2.0 |
4.6 |
|
900 以上 |
0.9 |
3.9 |
根据表 10–1 中的数据,作出如图 10–15 所示的 100℃ 时的氧分子在各速率区间速率分布的直方图,并与 0℃ 时的速率分布直方图作比较。
19 世纪中叶,英国物理学家麦克斯韦创造性地运用统计方法找到了气体分子速率的分布函数,从而确定了气体分子速率分布的统计规律。该分子速率分布函数 f(v) 的图像如图 10–16 所示。f(v)为在速率 v 附近单位速率间隔内气体分子数与分子总数的比。
图 10–16 麦克斯韦气体分子速率分布曲线
这个规律指出:一般而言,气体分子的速率各不相同,但大多数分子的速率都在某个数值(峰值)附近,离开这个数值越远,分子数越少,呈现出“中间多,两头少”的分布
特征;温度升高,曲线的峰值会向速率大的方向移动,速率的分布范围增大,整个曲线将变得较为平坦。
图 10-16 中的高温和低温时速率分布曲线下的面积是否相等,为什么?
对大量分子组成的系统,我们很难掌握每个分子运动的全部信息,运用统计方法可以获得大量分子的速率、动能等微观物理量遵循的统计规律,进而确定物体的宏观状态和性质。例如,根据气体的速率分布规律就可以确定气体的温度。随着人们对定量研究的日益重视,统计方法已被应用到自然科学和社会科学的众多领域。
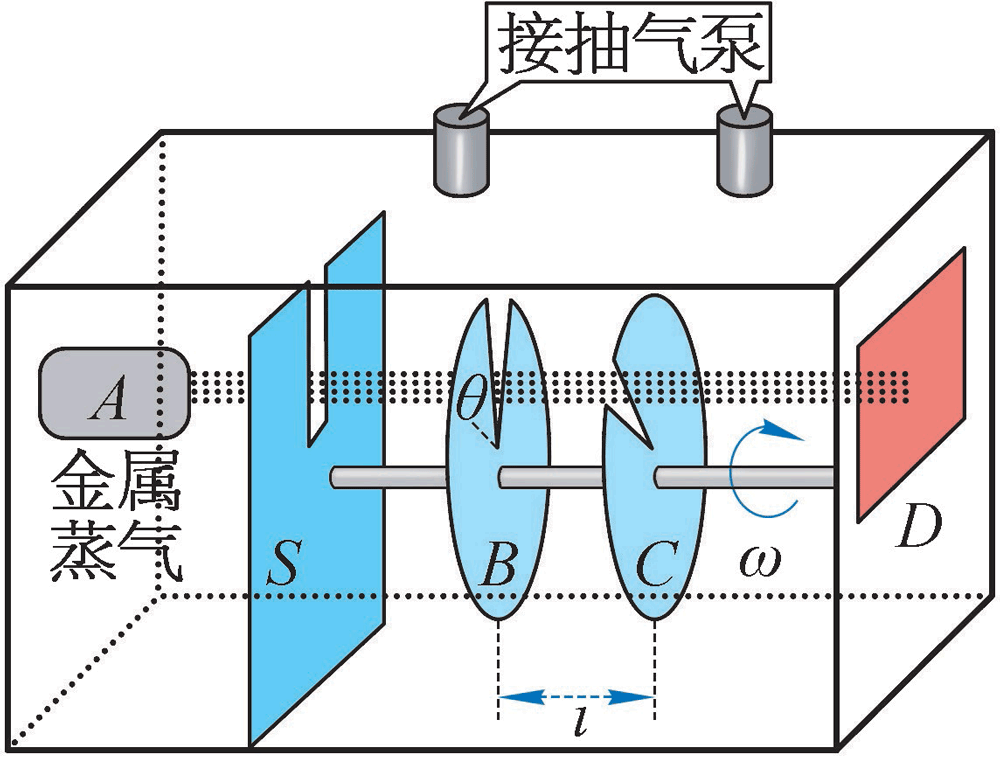
图 10–17 密勒和库士的实验装置示意图
麦克斯韦给出气体分子的速率分布规律后,由于高真空技术和测量技术的限制,此后近半个世纪都无法用实验验证这一统计规律。直到 1920 年,英国物理学家史特恩才做了第一次成功的尝试。1934 年,我国物理学家葛正权(1896—1988)改进了史特恩的实验装置,并定量地验证了麦克斯韦的气体分子速率分布规律,获得国际公认。
1955 年,哥伦比亚大学的密勒和库士提出了一个能高度精确证明这个分布律的实验方案。实验装置如图 10–17 所示。实验结果与麦克斯韦气体分子速率分布律完全相符。
- 判断以下关于分子速率的观点是否正确,并简述理由。
(1)当温度升高时,组成物体的每个分子的速率都会增大。
(2)甲、乙两杯水,甲杯水的温度为 70℃,乙杯水的温度为 30℃,那么甲杯水内的每个水分子的速率都比乙杯水内每个水分子的速率大。
- 在温度为 25℃ 的环境中,有一个导热良好的密闭容器内封有一定量的氮气。简述容器中氮气分子的速率分布情况。若将该容器放入冰箱冷藏室后,氮气分子的速率分布如何变化?
- 在日常生活中,很多现象都遵循统计规律。根据本年级所有同学的身高数据,分别作出本班男生(或女生)和全年级男生(或女生)身高的分布曲线,观察并比较两个曲线的形状;了解人数占比最多的身高区间。
本节编写思路
热现象是物质中大量分子无规则运动的集体表现;在学习了“分子动理论”之后,了解分子运动速率分布的统计规律有助于进一步研究热现象。
本节先以“伽尔顿板”的演示实验引出统计规律,然后借助氧分子速率分布的实验数据,在绘制直方图的基础上引出麦克斯韦气体分子运动速率分布规律。
通过本节学习,知道分子运动速率分布图像的物理意义,初步认识统计规律是大量偶然事件整体所遵循的规律。
正文解读
“伽尔顿板”实验的结果表明,大量小球落下时,落入某个槽中的小球的数目具有相对确定的值,这意味着尽管单个小球落入某个小槽的概率是确定的,但具体哪个时刻落入哪个小槽是不确定的,只有大量小球落入槽中稳定后,才有确定的分布。或者说,对由大量微观粒子组成的系统的宏观性质和规律而言,统计规律起主导作用。由此可知,统计规律与力学的决定性规律有着明显的差别:统计规律对大量偶然事件整体起作用,力学规律对单个事件起作用,统计规律并不是力学规律的简单叠加。另一方面,多次使很多小球一起下落时,落入下半部分各小槽中的小球数分布基本保持不变,而不是绝对相同。这说明在统计规律起主导作用的情况下,单个的偶然事件相对统计规律仍会有涨落。
此处设置“自主活动”,要求学生模仿绘制 100 ℃ 时氧分子在各速率区间速率分布的直方图,从而理解统计分布的规律,感受不同温度下速率分布的不同。
此处设置“大家谈”,是为了帮助学生进一步理解麦克斯韦气体分子速率分布曲线中纵坐标的含义,即 v ~ v + Δv 间隔内的分子数占总分子数的百分率。曲线下的总面积表示整个速率间隔(0 ~ ∞)的分子数占总分子数的百分率,所以数值等于 1。
问题与思考解读
1.参考解答:这两种说法都是错误的。
任何温度下,组成物体的分子都有从小到大各种速率。温度升高时,占比最多的分子对应的速率更大一些。
命题意图:理解分子速率分布的统计规律。
主要素养与水平:运动与相互作用(Ⅱ);科学论证(Ⅱ)。
2.参考解答:氮气分子都在做无规则运动,速率从小到大都有,但某含速率附近的速率区间内的分子数最多,离这个速率越远的速率区间内分子数越少。放入冷藏室内后,氮气分子的速率依然从小到大都有,但是速率分布会集中在较小的区域,分子数最多的区间转移到一个较小的速率附近,离这个速率越远的速率区间内分子数依然越少。
命题意图:在具体的情境中应用分子速率分布的统计规律描述气体及其变化。
主要素养与水平:运动与相互作用(Ⅱ)。
3.参考解答:略。
命题意图:研究生活现象中的统计规律,经历调查、搜集资料、处理数据等研究过程,并与同学交流。
主要素养与水平:证据(Ⅱ);交流(Ⅰ);科学态度(Ⅱ)。
资料链接
麦克斯韦分子速率分布
以气体为例,组成气体的每一个分子的运动速度的大小和方向都是偶然的、随机的,但从宏观整体的角度来看,由大量分子组成的气体都有一定的压强和温度。这表明这些大量偶然事件有一定的分布规律,这种微观上的千变万化、完全偶然,而宏观上具有一定规律的现象称为统计规律性。平衡态下热力学系统的粒子按速率分布的规律是麦克斯韦(J.C.Maxwell,1831—1879)在 1859 年应用统计概念首先导出的。
(1)麦克斯韦速率分布
设在平衡状态下,某气体的分子总数为 N,速率在 v ~ v + Δv 间隔内的分子数为 ΔN,则在速率 v 附近单位速率间隔内,气体分子数与分子总数的比 f(v) = \(\frac{{\Delta N}}{{N\Delta v}}\);对单个分子来说,它表示分子具有的速率在该单位速率间隔内的概率。麦克斯韦经过理论研究指出,在平衡状态下,气体分子速率分布函数的具体形式是:
\[f(v) = 4\pi {\left( {\frac{m}{{2\pi kT}}} \right)^{\frac{3}{2}}}{e^{ - \frac{{m{v^2}}}{{2kT}}}}{v^2}\]
式中 m 为一个分子的质量,k 为玻尔兹曼常数,T 为热力学温度。
表示速率分布函数的曲线叫做麦克斯韦速率分布曲线,如图 1 所示。从图 1 中可以看出,深色的小矩形的面积为 f(v) Δv = \(\frac{{\Delta N}}{N}\),表示某分子的速率在间隔 v ~ v + Δv 内的概率,也表示在该间隔内的分子数与总分子数的比。在不同的间隔内,有不同面积的小矩形,说明不同间隔内的分布不相同,面积较大表示分子具有该间隔内的速率的概率也较大。当 Δv 足够小时,无数个矩形的面积总和将趋近于曲线下的面积,这个面积表示分子在整个速率间隔的概率的总和,按归一化条件,应等于 1。
图 1
从速率分布曲线还可以知道,具有很大速率或很小速率的分子数较少,其所占的比例较低,而具有中等速率的分子数很多,其所占的比例很高。曲线上有一个最大值,与这个最大值对应的速率 vP 叫做最概然速率。它的物理意义是:在一定温度下,速率与 vP 相近的单位速率间隔内的气体分子所占的比例最大,也就是以相同速率间隔来说,气体分子中速率在 vP 附近的概率最大。温度升高时,气体分子的速率普遍增大,最概然速率 vP 也相应增大,但因曲线下的总面积是不变的,因此分布曲线在宽度增大的同时高度降低,整个曲线将变得“较平坦些”。
(2)分子速率的三个统计值
根据麦克斯韦速率分布律,可推算出处于热平衡态的热力学系统中的微观粒子的三个统计值:
最概然速率:vP = \(\sqrt {\frac{{2kT}}{m}} \)
平均速率:\({\bar v}\) = \(\sqrt {\frac{{8kT}}{{\pi m}}} \)
方均根速率:\(\sqrt {\overline {{v^2}} } \) = \(\sqrt {\frac{{3kT}}{m}} \)
图 2显示了在速率分布曲线上的三个统计值。当温度升高时,三个速率的统计值都随之增大,这三种速率在不同问题中有着各自的应用。在讨论速率分布时,要用到大量分子的最概然速率 vP;计算分子运动的平均自由程时,要用到平均速率 \({\bar v}\);计算分子的平均平动动能时,就要用方均根速率 \(\sqrt {\overline {{v^2}} } \)。
图 2
发布时间:2022/6/23 下午8:56:02 阅读次数:10330


