第十章 第七节 电功电功率及焦耳定律

图 10–60 电熨斗
用电器可以把电能转化成各种其他形式的能。电熨斗(图 10–60)、电热毯、电饭煲和工业上用来冶炼钢铁的电弧炉,主要把电能转化成内能;洗衣机、电车主要把电能转化成机械能;电解池、电镀装置主要把电能转化成化学能。我们知道,从一种形式的能转化成另一种形式的能的过程需要做功。电能转化成其他形式的能的过程实际上就是电流做功的过程。
我们把电流所做的功叫做电功(electric work)。电流做了多少功就表示有多少电能转化成其他形式的能。
电功实质上是导体中的电场对自由电荷的作用力做的功。设通过导体的恒定电流为 I,导体两端的电压为 U,则在时间 t 内电流通过这段导体的电荷量为 q = It,电场力对电荷所做的功为
W = qU = UIt
电功的单位是焦耳,简称焦,符号是 J。
以前已经学过用功率表示机械做功的快慢,类似的,我们用电功率来表示电流做功的快慢。电流所做的功与完成这些功用的时间之比叫做电功率(electric power),用 P 表示。根据功率的定义式 P = \(\frac{W}{t}\),将 W = UIt 代入得
P = UI
电功率的单位是瓦特,简称瓦,符号是 W。
日常生活使用的电器上都贴有一个铭牌,标识该用电器的额定电压、额定功率或额定电流等。如图 10–61 所示是一台电风扇的铭牌,说说铭牌上标识的电学量及其含义。
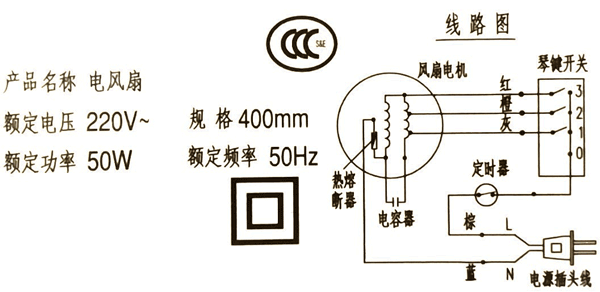
图 10–61 某电风扇的铭牌
示例 1 一浴霸的额定功率 P = 1.1 kW、额定电压 U = 220 V。试问:该浴霸在正常工作时,通过的电流有多大?如果连续正常工作 30 min,消耗多少电能?
分析:电流可由 I = \(\frac{P}{U}\) 求解,消耗的电能即为这段时间电流做的电功。
解:设浴霸正常工作时电流为 I,则根据电功率的公式 P = UI,可得
\[I = \frac{P}{U} = \frac{{1\;100}}{{220}}\;{\rm{A}} = 5\;{\rm{A}}\]
浴霸连续正常工作时间 t = 30 min = 1 800 s,消耗电能
\[W = Pt = 1\;100 \times 1\;800\;{\rm{J}} = 1.98 \times {10^6}\;{\rm{J}}\]
需要说明的是,由于焦耳这个单位较小,在日常生活中经常使用的电功单位是千瓦·时(kW·h)。1 kW· h 等于电功率为 1 kW 的用电器连续工作 1 h 所消耗的电能。因此,如需知道示例 1 中的浴霸消耗了多少千瓦·时电能,可由运行时间 t = 30 min = 0.5 h 及额定功率 P = 1.1 kW,得浴霸消耗电能
\[W = Pt = 1.1 \times 0.5\;{\rm{kW}} \cdot {\rm{h}} = 0.55\;{\rm{kW}} \cdot {\rm{h}}\]
英国物理学家焦耳(J. P. Joule,1818—1889)经过多次实验指出:电流通过导体产生的热量 Q,与电流 I 的二次方、导体的电阻 R 和通电的时间 t 成正比。这就是焦耳定律(Joule’s law),即
\[\color{#975F85}Q = {I^2}Rt\]
通常把电流流过导体时产生的热量称为电热,也叫做焦耳热。电流通过导体产生的热量与所用时间之比叫做热功率,其表达式为
\[\color{#975F85}P = \frac{Q}{t} = {I^2}R\]
电路将消耗的电能全部用于发热,这样的电路称为纯电阻电路,典型的应用有电熨斗、电饭煲等。
示例 2 一台标有“ 220 V 1 000 W” 字样的电热水器在额定电压下使用,1 min 产生多少热量?如果电路电压略有下降,降为 210 V,电热水器 1 min 放出的热量又是多少?
分析:电热水器的电路可视作纯电阻电路,电功率等于热功率。当电压不是额定电压时,电热水器的实际功率就不是额定功率 1 000 W。
解:设该电热水器额定电压为 U、额定功率为 P、电阻为 R,则其 1 min 产生的热量
\[Q = Pt = 1\;000 \times 60\;{\rm{J}} = 6.9 \times {10^4}\;{\rm{J}}\]
根据 P = UI = \(\frac{{{U^2}}}{R}\),可得电热水器的电阻
\[R = \frac{{{U^2}}}{P} = \frac{{{{220}^2}}}{{1\;000}}\;\Omega = 48.4\;\Omega \]
当电路电压 U1 为 210 V 时,电热水器 1 min 产生的热量
\[{Q_1} = \frac{{U_1^2}}{R}t = \frac{{{{210}^2}}}{{48.4}} \times 60\;{\rm{J}} \approx 5.5 \times {10^4}\;{\rm{J}}\]
由本示例可知,用电器只有在额定电压下,其电功率才是额定功率,如果电压发生变化,实际功率就会发生变化。
如果电路是纯电阻电路,电能都转化为内能,这时电功 W 与电流所产生的热量 Q 相等,即 W = Q。
如果电路中有电动机或电解槽等用电器,则在这类非纯电阻电路中,电能并不全都转化为内能,有部分电能转化为机械能或化学能。这时,电功 W > 电热 Q,它们的差就是电能转化成机械能或化学能的部分。
示例 3 一台电动机的额定电压 U = 220 V,线圈的电阻 R = 0.8 Ω。正常工作时,它每秒产生的热量为 1 280 J,则正常工作时的电流为多大?电动机的输出功率为多大?
分析:含有电动机的电路是非纯电阻电路,电能会转化为内能和机械能。应先根据电动机产生的热量算出通过线圈的电流 I;再根据电功率的公式 P = UI 算出电动机的输入功率 P,将输入功率减去转化为内能的功率 P 热,就是电能转化为机械能的功率,也即输出功率 P 输出。
解:设电动机正常工作时通过的电流为 I,1 s 产生的热量为 Q,则由 Q = I2Rt 得
\[I = \sqrt {\frac{Q}{{Rt}}} = \sqrt {\frac{{1\;280}}{{0.8 \times 1}}}\; {\rm{A}} = 40\;{\rm{A}}\]
电动机正常工作时输入功率
\[P = UI = 220 \times 40\;{\rm{W}} = 8\;800\;{\rm{W}}\]
电动机正常工作时的热功率
\[{P_热} = \frac{Q}{t} = \frac{{1\;280}}{1}\;{\rm{W}} = 1\;280\;{\rm{W}}\]
因此,电动机的输出功率
\[{P_{输出}} = P - {P_热} = (8\;800 - 1\;280)\;{\rm{W}} = 7\;520\;{\rm{W}}\]
- 在力学和电学的学习中,已经知道功率的多种表达式,简要说明下述表达式的含义及其适用范围:
① P = \(\frac{W}{t}\) ② P = Fv ③ P = UI ④ P = I2R ⑤ P = \(\frac{{{U^2}}}{R}\)
- 一台电热水器接入电压为 220 V 的电路中,0.5 h 内产生的热量为 1.452×106 J,求这台热水器加热时的电阻。
- 一台电动机额定电压是 220 V,线圈电阻为 0.5 Ω,电动机在正常工作时通过的电流为 32 A,则电动机在运转 20 min 的过程中,消耗了多少电能?线圈电阻产生了多少热量?最多有多少电能转化为机械能?
- 一台冰箱的输入功率是 180 W,一天耗电 1 kW·h。若冰箱每次制冷时间为 7 min,且间隔均匀相等,估算该冰箱 1 h 制冷的次数。
- 移动电源,也叫“充电宝”,常采用锂电芯,能为手机、平板计算机等设备供电,但使用不当可能会造成过充、短路等安全隐患。出于安全原因,中国民航
表 10–4
|
输入 |
DC 5 V 2.0 A |
|---|---|
|
输出 |
DC 5 V 2.1 A |
|
容量 |
10 000 mA·h |
|
转换率 |
>85% |
总局规定当移动电源的能量不超过 100 W·h 才可在乘机时随身携带。某移动电源的铭牌如表 10–4 所示。
(1)通过计算,判断乘客在乘机时是否能随身携带该移动电源。
(2)该移动电源在充满电的情况下,能为一个“3 W 1.5 A”的 USB 风扇供电多长时间?
本节编写思路
本节在电学量、电路连接方式、电路相关规律的基础上,进一步学习电路中能量的转化问题,进一步建立完善能量的观念。
电功和电功率的概念建立时多与机械功和功率相类比,凸显类比的方法。
通过电功与电热的比较,明确纯电阻电路与非纯电阻电路的区别,理解各公式的意义与适用条件。将额定功率与实际功率相比较,理解两者的区别与联系。
正文解读
电熨斗是一个常见的家用电器,也是一个电热设备。
此处的“大家谈”活动,也可以让学生收集家中的电器铭牌上的标识信息在课堂上交流。
示例 1 可让学生熟悉电功率公式的使用,了解生活中常用的电能单位。
示例 2 让学生通过具体的运算了解额定功率与实际功率的区别。
示例 3 让学生了解非纯电阻电路的电功率的运算,从而更好地理解输入功率、热功率、输出功率的含义。
问题与思考解读
1.参考答案:① 功率的定义式,适用于任何功率的计算 ② 功率的计算式,适用于力做功的功率计算 ③ 电功率的定义式,电功率的计算均适用 ④⑤ 热功率的计算式,仅适用于纯电阻电路发热功率的计算??。
命题意图:加深对各公式的理解。
主要素养与水平:能量观念(Ⅰ);科学论证(Ⅱ);科学本质(Ⅰ)。
2.参考答案:R = U2t/W = 2202 ×1 800 ÷(1.452 × 106)Ω = 60 Ω。
命题意图:熟悉电功公式的使用。
主要素养与水平:能量观念(Ⅰ);模型建构(I);科学推理(Ⅱ)。
3.参考答案:W输入 = UIt = 220 × 32× 20 × 60 J = 8.448 × 106 J,W热 = I2Rt = 322 × 0.5 × 20 × 60 J = 6.144 × 105 J,W机 = W输入 – W热 = 7.833 6 × 106 J。
命题意图:非纯电阻电路的计算。
主要素养与水平:能量观念(Ⅱ);模型建构(Ⅱ);科学推理(Ⅱ)。
4.参考答案:约为 2 次。N = W/P·t = 3.6 × 106 ÷ 180 ÷ 420 = 47.6,n = N/24 ≈ 2。
命题意图:将学到的知识应用于实际生活。
主要素养与水平:能量观念(Ⅰ);模型建构(Ⅰ);科学推理(Ⅰ);社会责任(Ⅰ)。
5.参考答案:(1)该充电宝的能量为 50 W·h,所以可以携带。
(2)14.2 h(注意:此题用 t = W/P 和 t = q/I 两种方法做出的答案不同,疑似给的数据不自洽)
命题意图:根据所学知识读懂身边常用电器技术参数的含义,养成安全意识。
主要素养与水平:模型建构(Ⅰ);科学推理(Ⅱ);科学论证(Ⅱ);社会责任(Ⅱ)。
资料链接
直流电动机的基本结构、功率和效率
直流电动机是将电能转化为机械能的旋转机械装置。在生产、工业领域主要运用的是交流电动机,但由于直流电动机有较好的启动和调速性能,常被用在对启动和调速有较高要求的场合,如矿井卷扬机、高速电梯、电动汽车等。
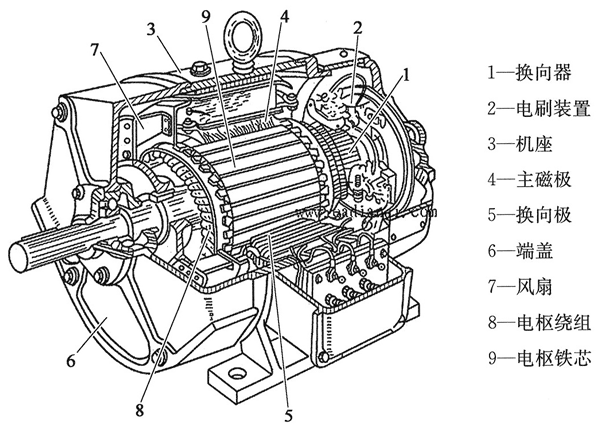
直流电动机由定子和转子两部分组成,结构如图 14 所示。定子是指直流电动机工作时静止不动的部分,主要包括主磁极、换向极、电刷、机座、端盖和轴承等。转子则是指直流电动机的运动部分,它是产生感应电动势及电磁转矩,从而实现能量转化的重要部分,因此又被称为电枢,由转轴、电枢铁芯、电枢绕组、换向器等组成。
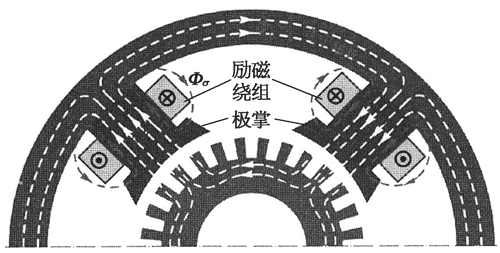
主磁极是用来在电动机中产生磁场的,结构如图 15 所示,包括极心和极掌两部分,极心上有励磁绕组,极掌为其下方扩大部分,用来使电机空气隙中磁感应强度分布最为合适。
电枢铁芯为圆柱形,表面有槽,电枢绕组一般由铜线绕成,包上绝缘后嵌入电枢铁芯的槽中。
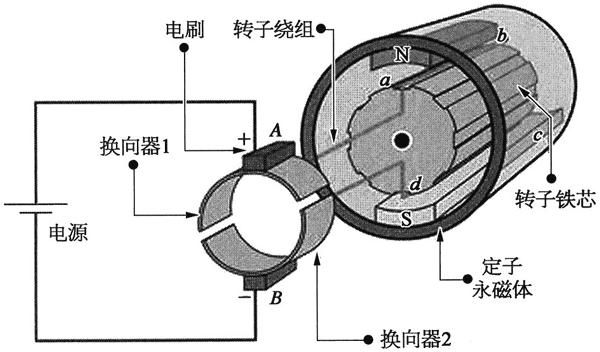
为了明确电动机中换向器与电刷的作用,我们将直流电动机的主磁极和电枢绕组等部分进行简化,结构如图 16 所示,电刷 A、B 与换向器相连接,电流在电枢绕组中的电流流向为 a → b → f → d,因此产生顺时针的电磁转矩,当 ab 边和 cd 边旋转超过与中轴在同一个水平面后,电刷 A 将与换向器 2 连接,电枢绕组中的电流转变方向,但是产生的电磁转矩不变,使其继续转动。所以,换向器的作用就是改变电枢绕组中的电流,使电磁力维持电枢的转动。
另外,当电枢在磁场中转动时,根据电磁感应,电枢绕组也会产生感应电动势。这一电动势的方向与外加电压的方向相反,被称为反电动势。当电动机工作时,电动机的电磁转矩 T 应该与机械负载转矩 T1 与空载损耗转矩 T0 相平衡;当负载增加时,即 T1 增加,此时机械负载转矩 T1 与空载损耗转矩 T0 大于电磁转矩 T,电动机转速将下降,此时电枢中的反电动势也将下降,从而使得电枢电流增加(Ia = \(\frac{{U - E}}{{{R_a}}}\),式中 E 为反电动势,U 为电动机两端电压,Ia、Ra分别为电枢的电流及电阻),若电动机的两端电压不变,则其输入功率将增大。这就表明直流电动机的功率会随转速的变化而变化。
在选择电动机时,应该考虑其效率、转速和功率等因素。电动机的效率可用字母“η”表示,等于电动机输出功率 P2 与电动机输入功率 P1 之比的百分数,即 η = (P2/P1) × 100%。
电动机的效率与拖动的负载、电动机的转速和电源的电压都有关系。一般直流电动机效率在 80% ~ 85% 左右,负载小时效率低,负载大时效率高。
发布时间:2022/5/28 上午10:09:19 阅读次数:10136
