第十章 第三节 测量金属丝的电阻率

图 10–20 汽车后挡风玻璃上的电阻丝
细心观察,你会发现汽车的后挡风玻璃上有一条条的细线,如图 10–20 所示,其实这些细线是金属电阻丝。当挡风玻璃起雾、起霜时,汽车对挡风玻璃上的电阻丝通电加热可以起到除雾化霜的作用。我们已经知道金属丝的长度和横截面积一定时,其阻值取决于金属材料的电阻率。本节我们将通过实验测量金属丝的电阻率。
若有一根长为 L、直径为 d 的金属丝,则可以根据电阻定律 R = ρ \(\frac{L}{S}\),得其电阻率 ρ = \(\dfrac{{SR}}{L}\),又 S = π\({\left( {\dfrac{d}{2}} \right)^2}\),所以可得
\[\rho = \frac{{\pi {d^2}R}}{{4L}}\]
因此,要测得金属丝的电阻率 ρ,需要先测得金属丝的长度 L、直径 d 和电阻 R。
学生实验一:长度测量及其测量工具的选用
长度是物理学中的基本物理量之一。长度的测量是最基本的测量,测量工具众多,最常用的工具是刻度尺。另外,也可以使用游标卡尺(图 10–21)和螺旋测微器(图 10–22)等。测量工具的分度值(测量工具所能测量的最小值)决定了测量工具所能达到的精度。通常情况下,刻度尺的分度值为 1 mm,游标卡尺的分度值有 0.1 mm、0.05 mm 和 0.02 mm 三种,螺旋测微器的分度值一般为 0.01 mm。
图 10–21 数字显示游标卡尺
图 10–22 数字显示螺旋测微器
测量长度时要根据不同的场景和要求选择不同的工具。应尽量选择测量工具的量程大于被测物体长度,避免多次测量的累加造成的测量精确度下降;测量工具的分度值要小于测量精度的要求。如金属丝的长度可用刻度尺测量,但金属丝的直径用刻度尺测量则满足不了精度的要求,会造成较大的误差,因此需要选用精度更高的游标卡尺或螺旋测微器对金属丝直径进行测量。
实验原理与方案
用刻度尺测量金属丝的长度,用数字显示螺旋测微器测量金属丝的直径。多次测量取平均值以减少误差。
实验操作和数据收集
1. 用刻度尺测量金属丝的长度,将数据记录在表 10–3 中;
2. 用数字显示螺旋测微器测量金属丝横截面的直径。打开电源开关,在测砧与测微螺杆接触时进行调零;将金属丝置于测砧与测微螺杆之间;旋转旋钮,当测砧即将夹紧金属丝时,改旋微调旋钮使测砧夹紧金属丝,将显示屏上显示的金属丝直径数值记录在表 10–3 中。
表 10–3 实验数据记录表
|
实验序号 |
1 |
2 |
3 |
4 |
5 |
平均值 |
|---|---|---|---|---|---|---|
|
金属丝长度 l/mm |
|
|
|
|
|
|
|
金属丝直径 d/mm |
|
|
|
|
|
|
实验结论
金属丝的长度 l 为 _________________;金属丝的直径 d 为 ___________________。
交流与讨论
也可用游标卡尺测金属丝的直径。各组交流使用不同测量仪器的体会,讨论提高测量准确度的方法。
1.游标卡尺的测量原理
游标卡尺作为一种被广泛使用的高精度测量工具,可以测量物体的长度、内径、外径及深度等。它是由主尺和附在主尺上能滑动的游标尺两部分构成,如图 10–23 所示。游标尺上的刻度线越多,测量的精确程度就越高。如分度值为 0.1 mm、0.05 mm、
图 10–23 游标卡尺
0.02 mm 的游标卡尺的游标尺上分别有 10 条、20 条、50 条刻度线。那么,游标卡尺是如何实现测量精度的提高的呢?
游标尺上的刻度间距 x 比主尺上的刻度间距 y 略小一点。一般游标尺上的 n 个刻度间距等于主尺上(n − 1)个刻度间距,即
nx = (n − 1)y
由此可知,游标上的刻度间距与主尺的刻度间距相差 \(\frac{1}{n}\) mm,这就是游标尺的精度。以分度值 0.1 mm 的游标卡尺为例,如图 10–24 所示,游标尺上有 10 个等分刻度,总长 9 mm,因此游标尺的每一分度为 0.9 mm,比主尺上的最小分度小 0.1 mm。当测量爪并拢时,主尺和游标尺的零刻度线对齐,两者的第一条刻度线相差 0.1 mm,第二条刻度线相差 0.2 mm,……,第 10 条刻度线相差 1 mm,即游标的第 10 条刻度线恰好与主尺的 9 mm 刻度线对齐。若测量时测量爪的卡口间距为 0.3 mm,游标尺就要向右移动 0.3 mm,使得它第 3 条刻度线恰好与尺身的 3 mm 刻度线对齐。这样就将主尺上读数时所涉及的估读问题转化为确定主尺上的刻度线与游标尺上的哪条刻度线对齐的问题。所以,游标卡尺是利用主尺的单位刻度(1 mm)与游标尺的单位刻度之间固定的微量差值来提高测量精度的,即采取了错位放大法提高了测量的精度。
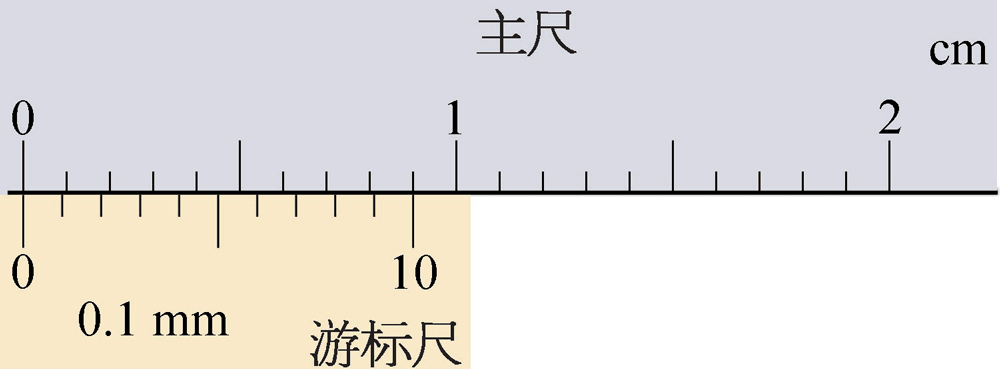
图 10–24 分度值为 0.1 mm 的游标卡
尺的刻度线

图 10–25 分度值为 0.02 mm 的游标
卡尺的读数
如图 10–25 所示的游标卡尺的精度为 \(\frac{1}{50}\) mm,即 0.02 mm。在读数时,先从主尺上读得游标尺的零刻度线所在的整数分度值(25 mm);再到游标尺上找与主尺刻度线准确对齐的游标刻度线(第 11 根刻度线);求得游标尺的分度值 11×\(\frac{1}{50}\) = 0.22 mm;最后得到测量值 25 + 0.22 = 25.22 mm。由于使用游标卡尺测量长度时没有进行估读,只是判断刻度线的对齐与否,因此其测量误差即为游标尺的精度值,本例中为 0.02 mm。
2.螺旋测微器的测量原理
螺旋测微器[图 10–26(a)]是依据螺旋放大的原理制成的。该原理类似于在盘旋式楼梯上行走时,走过的距离与上升高度间存在放大关系,即螺杆在螺母中旋转一周的同时即沿着旋转轴线方向前进(后退)一个螺距的距离。在螺旋测微器中,可动
刻度的一圈为 50 格,而旋转一圈,螺杆前进(后退)0.5 mm,即为固定刻度中的一小格,所以,螺旋测微器可精确测量的最小刻度为 \(\frac{0.5}{50}\) mm = 0.01 mm。

(a)实物
(b)读数
图 10–26 螺旋测微器
如图 10–26(b)所示的螺旋测微器(局部)螺距为 0.5 mm,活动套筒(可动刻度)的周界被等分为 50 格,故活动套筒转动 1 格,螺杆相应地移动 0.01 mm,再加上估读,其测量精度值可达到 0.001 mm。读数时,先读固定套筒(刻度)上标尺的数值,再加上活动套筒上标尺的数值。应特别注意活动套筒上的示数是否过 0,过 0 则加 0.5,不过 0 则不能加 0.5。如图10–26(b)所示,虽然固定套筒上的 5.5 mm 刻度线已经可以看到,但活动套筒上的示数尚未过 0,因此读数应为 5.0 + 0.474 = 5.474 mm,而非 5.5 + 0.474 = 5.974 mm。
学生实验二:测量金属丝的电阻率
实验原理与方案
图 10–27 实验电路图
要测得金属丝的电阻率,在金属丝的长度和直径的测量基础上,还需要进一步测出金属丝的电阻 R。本实验采用伏安法测量金属丝阻值 R,电路图如图 10–27 所示。
实验装置与方法
本实验要用到学生稳压电源、电压表、电流表、滑动变阻器、待测金属丝等实验器材。
实验操作和数据收集
根据图 10–27 连接电路,闭合开关,调节滑动变阻器,设计表格,记录多组电压、电流值。
数据分析
根据实验数据,绘制 U–I 图像,由图线的斜率得出金属丝的阻值 R。
根据测得的金属丝长度、直径和阻值计算金属丝的电阻率。
实验结论
金属丝的电阻率 ρ = ______________。
交流与讨论
与其他实验小组分享、比较同一金属丝电阻率的测量结果,并通过查表对比标准值与所测金属丝电阻率的差异。
分析实验误差产生的原因,提出减少实验误差的方法。
把各种材料的电阻率由小到大排列起来,如图 10–28 所示。

图 10–28 各种材料的电阻率
可见,锗、硅、硒、氧化铜、硼等的电阻率比绝缘体小而比金属大,这类材料称为半导体。
图 10–29 电子体温计
半导体的电阻率常随周围各种环境条件的改变而变化。利用半导体的电阻率随温度升高而减小的特性,可以制成热敏电阻。如图 10–29 所示是一个用热敏电阻制成的半导体体温计,灵敏度、精确度都比较高。
热敏电阻还广泛应用于电子器件的自动调节和控制,是自动化设备的一种重要元件。
有的半导体材料在光照下,电阻率也会改变,这类半导体材料可制成光敏电阻。它也是自动控制、遥测技术中的重要元件。例如,若机器上装有光敏电阻控制的制动装置,使一束光照射在光敏电阻上,操作时,若手伸入了危险区,光路就被截断,光敏电阻阻值迅速增大。通过控制电路,机器立刻自动停止运转,从而保证操作工人的安全。在货物传送带旁安装光敏电阻控制的计数器,就可对货物自动计数。
- 根据“测量金属丝的电阻率” 的实验,判断下列操作是否正确,并对错误的操作做出修改。
(1)用刻度尺多次测量金属丝的全长,算出其平均值。
(2)用螺旋测微器在金属丝上一个部位测量直径。
(3)实验中尽可能保持金属丝的温度不变。
- 某段导线的电阻是 2 Ω,如果把它均匀拉长到原来的 1.2 倍,这段导线的电阻将变为多少?
- 某同学为了测定自动铅笔笔芯的电阻率做了以下实验:他取出一根直径为 0.7 mm 的自动铅笔笔芯,用刻度尺测出笔芯的长度为 11.0 cm,又用“伏安法”测得其电阻阻值为 25.1 Ω。计算铅笔芯的电阻率并提出 1 ~ 2 个在实验中可能产生误差的原因。
- 将若干张相同的纸叠放在一起,用刻度尺测量出其总厚度,然后除以张数,可以得到一张纸的厚度。受此方法启发,如何用刻度尺测出一根细电阻丝的直径?写出测量方法,并用字母表示出测量值。若该电阻丝的总电阻为 R,总长度为 l,试写出该电阻丝的电阻率的表达式。
- 长江口涨潮时海水倒灌,出现所谓“咸潮”现象,使得崇明岛的水质受到影响。如果海水的电阻随长度、横截面积的变化规律与金属导体相同。设计一个测量海水电阻率的实验方案以研究“咸潮”出现的规律。
本节编写思路
本节学习落实课标“3.2.2 会测量金属丝的电阻率”的要求。上节电阻定律的学习是本节测量金属丝电阻率的理论基础。要注意区分两节课实验的区别:上节课是探究影响金属导体电阻的因素,得出电阻定律;本节是利用电阻定律测量某种材料金属丝的电阻率。
通过理论分析得知,要测量金属丝的电阻率先应测量金属丝的长度、直径和电阻,然后相应地进行学生实验一、二。
通过动手实验,学习工具的使用,进行实验误差的分析,减小实验谡差的讨论,培养严谨求实的科学态度。
正文解读
现在家用汽车已经相当普及,节首图所描述的与电阻率有关的现象,教师可以拍一段视频更好地体现电阻丝的除雾、除霜的功能。
关于“拓展视野”给出的游标卡尺和螺旋测微器的原理,学生从中可以学习和借鉴解决问题的思维方法。
学生实验一和学生实验二其实是电阻率测量实验的两个部分,教材为了呼应课程标准的要求,拆分为两个独立的实验。
问题与思考解读
1.参考解答:(1)正确 (2)错误,应该在多个部位进行测量并取平均值 (3)正确。
命题意图:知道测量时的注意事项,减少误差。
主要素养与水平:证据(Ⅱ);科学态度(Ⅰ)。
2.参考解答:2.88 Ω(长度拉长到 1.2 倍,由于导线的体积不会改变,所以横截面积缩小到 \(\frac{1}{{1.2}}\),根据电阻定律导电的电阻将变为原来的 1.44 倍)
命题意图:熟悉电阻定律的应用。
主要素养与水平:物质观念(Ⅰ);模型建构(Ⅰ);科学推理(Ⅰ)。
3.参考解答:ρ = RS/l = 25.1 × 3.14 × (0.35 × 10−3)2 ÷ 0.11 Ω·m = 8.78 × 10−5 Ω·m。
实验中测量笔芯长度、用伏安法测量笔芯电阻等会产生误差。
命题意图:电阻率的测量及误差分析。会用电阻定律进行计算。
主要素养与水平:模型建构(Ⅱ);科学推理(Ⅱ);证据(Ⅰ)。
4.参考解答:找一支圆铅笔(或粗细适当的圆柱体),将金属丝在铅笔上依次密绕适当的圈数,用刻度尺量出这个线圈的长度,再将线圈长除以圈数,所得的商就是金属丝的直径 d。
\[\rho = \frac{{R\pi {{\left( {\frac{d}{2}} \right)}^2}}}{l}\]
命题意图:了解测量长度的特殊法,熟悉电阻定律的计算。
主要素养与水平:模型建构(Ⅱ);科学推理(Ⅱ)。
5.参考解答:用玻璃管装满海水,两端密封接上电极进行测量(具体步骤略)
命题意图:与实际问题相结合,培养用所学知识解决实际问题的能力。
主要素养与水平:模型建构(Ⅱ);证据(Ⅱ);解释(Ⅱ);社会责任(I)。
资料链接
间接测量长度的多种方法
长度测量是最基本的测量。一般情况下,可以用测量工具刻度尺直接测量。如果受到某些条件的限制,不能或不易用测量工具直接测量,则可用间接测量方法。间接测量长度的方法通常有以下几种:
一、累积法
通过积少成多的办法进行测量,再通过求平均来求得相应的长度。这种方法还可以减小误差。可用于测纸的厚度和细金属线的直径。如要测某一本书每张纸的厚度,可取若干张纸(纸的张数要适量),压紧后,用最小刻度为毫米的刻度尺量出其总厚度,然后将总厚度除以纸的张数,所得的商即是每张纸的厚度。
又如,要测细金属丝的直径,我们只要找一支圆柱形铅笔(或粗细适当的圆柱体),将金属丝在铅笔上依次密绕适当的圈数,用有毫米刻度的刻度尺量出这个线圈的长度,再将线圈长除以圈数,所得的商就是金属丝的直径。
二、化曲为直法
曲线的长度是不易直接测出的,但可以将曲线化为直线.再用工具测出直线长。例如,测地图上某两城市铁路线的长度,可使棉线与地图上的铁路线重合,再把棉线拉直,用刻度尺测出其长度,即是地图上铁路线的长度。
三、滚轮法
比较长的曲线,可用一轮子沿曲线滚动,记下滚动的圈数,再测出其直径,然后求出其周长,最后将轮的周长与轮滚动的圈数相乘,所得的积就是曲线的长度。例如,要测运动场上跑道的长度,可用已知周长的滚轮在长跑道上滚动,用滚动的圈数 × 滚轮的周长,就可算出跑道的长度。
四、平移法
这种测量方法也叫“卡测法”。卡测法适用于部分形状规则的物体,某些长度端点位置模糊,或不易确定,如圆柱体、乒乓球的直径和圆锥体的高等,需要借助于三角板或桌面将待测物体卡住,把不可直接测量的长度转移到刻度尺上,从而直接测出该长度。例如,用直角三角板和刻度尺测球体的直径、圆锥体的高和圆柱体的直径等。
五、比例法
根据相似三角形的对应线段成比例,利用已知的长度求出未知的长度。例如,用竹子在晴天测量一幢楼房的高度,就是利用竹子的长与楼房的高的比等于它们的影子长度之比;飞机、轮船利用俯角和仰角以及一些已知的距离可求出未知距离的长度。
六、取样法
这种测量方法被称为“量小求大法”。由于被测量物体的长度远远超过了刻度尺的最大测量值,不便于用刻度尺测量,可先选取一个小物体或一小部分,用刻度尺测取其长度,然后设法测出大物体与小物体(或小部分)的倍数关系,最后根据这一倍数关系求得大物体的长度。
例如:测一大卷粗细均匀的细铜线的长度。由于细铜线长度数值非常大,远远超出了普通刻度尺的最大测量值,不便于直接测量。我们可以先截取一小段细铜线,用刻度尺测出其长度为 L,然后用天平分别测出所有细铜线的质量和截取的小段细铜线质量,两者相除求得其倍数关系为 n,则这一大卷细铜线的总长度为 nL。
伏安法测电阻及误差分析
【原理】
伏安法测电阻是电学的基础实验之一。它的原理是欧姆定律。根据欧姆定律的变形公式 R = \(\frac{U}{I}\) 知,要测某一电阻 Rx 的阻值,只要用电压表测出 Rx 两端的电压,用电流表测出通过 Rx 的电流,代入公式即可计算出电阻 Rx 的阻值。
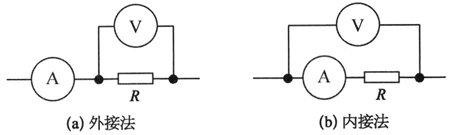
【内接法与外接法】
由于所用电压表和电流表都不是理想电表,即电压表的内阻并非趋近无穷大,电流表也存在内阻,因此实验测量出的电阻值与真实值不同,存在误差。为了减少测量过程中的系统误差,通常伏安法测电阻的电路有两个基本连接方法:电流表内接法和电流表外接法(图 2),简称内接法和外接法。
【误差分析】
外接法:
误差分析方法一:
在如图 3 所示的外接法中,考虑电表内阻的存在,则电压表的测量值 U 为 R 两端的电压,电流表的测量值为干路电流 I,即流过待测电阻的电流与流过电压表的电流之和,此时测得的电阻 R测 为 R 与 RV 的并联总电阻,即 R测 = \(\frac{U}{I}\) = \(\frac{{{R_{\rm{V}}} \times R}}{{{R_{\rm{V}}} + R}}\) < R(电阻的真实值)
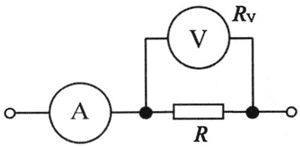
此时给测量带来的系统误差来源于 RV 的分流作用,系统的相对误差为:
\[\delta = \frac{{\left| {{R_测} - R} \right|}}{R} \times 100\% = \frac{1}{{1 + \frac{{{R_{\rm{V}}}}}{R}}} \times 100\% \tag{1}\label{1}\]
误差分析方法二:
当用外接法时,U测 = U真,I测 = IV + I真 > I真
所以,测出电阻值 R测 = \(\frac{{{U_测}}}{{{I_测}}}\) = \(\frac{{{U_真}}}{{{I_{\rm{V}}} + {I_真}}}\) < R真,即电压表起到分流作用,当 R 越小时,引起误差越小,说明该接法适应于测小电阻。
内接法:
误差分析方法一:
在如图 4 所示的内接法中,电流表的测量值为流过待测电阻和电流表的电流,电压表的测量值为待测电阻两端的电压与电流表两端的电压之和,即
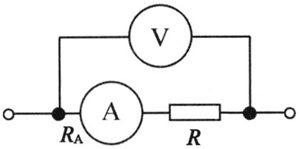
R测 = \(\frac{U}{I}\) = RA + R > R(电阻的真实值)
此时给测量带来的系统误差主要来源于 RA 的分压作用,其相对误差为:
\[\delta = \frac{{\left| {{R_测} - R} \right|}}{R} \times 100\% = \frac{{{R_{\rm{A}}}}}{R} \times 100\% \tag{2}\label{2}\]
误差分析方法二:
当用内接法时,I测 = I真,U测 = UA + U真 > U真
所以,测出电阻值 R测 = \(\frac{{{U_测}}}{{{I_测}}}\) = \(\frac{{{U_{\rm{A}}} + {U_真}}}{{{I_真}}}\) > R真,即电流表起了分压作用。当 RA 越小时引起误差越小,说明该接法适应于测大电阻。
【如何选择内接法与外接法】
一、根据待测电阻大小选择
从前面的分析可以知道,当 RV ≫ R 时,选择电流表外接法误差更小;当 RA ≪ R 时,选择电流表内接法误差更小。但这只给定了待测电阻 R 的一个大概的取值范围,在具体的测量中究竟如何根据给定的待测电阻 R 的值来确定测量电路的选择呢?
由 ①、② 式可知,伏安法测电阻时的相对误差不仅与电流表和电压表的内阻有关,而且与待测电阻的大小也有关。这里我们可以使内接法和外接法分别测电阻时两相对误差相等,即 \(\frac{1}{{1 + \frac{{{R_{\rm{V}}}}}{R}}}\) = \(\frac{{{R_{\rm{A}}}}}{R}\)
计算处理可得:R = \(\frac{{{R_{\rm{A}}} + \sqrt {R_{\rm{A}}^2 + 4{R_{\rm{A}}}{R_{\rm{V}}}} }}{2}\)
考虑到 RA ≪ RV,则有 R = \(\sqrt {{R_{\rm{A}}} \cdot {R_{\rm{V}}}} \)
由此可对内、外接法的选择作如下判断:
当 R = \(\sqrt {{R_{\rm{A}}} \cdot {R_{\rm{V}}}} \) 时,内接法和外接法测电阻的相对误差相等;当 R > \(\sqrt {{R_{\rm{A}}} \cdot {R_{\rm{V}}}} \) 时,采用内接法测电阻产生的误差较小;当 R < \(\sqrt {{R_{\rm{A}}} \cdot {R_{\rm{V}}}} \) 时,采用外接法测电阻产生的误差较小。
小结:用伏安法测电阻时,对于连接方法的选择遵循“大内大、小外小”的准则,即若待浏电阻为大电阻,则选用内接法,测量值与真实值相比偏大;若待测电阻为小电阻,则选用外接法,测量值与真实值相比偏小。
二、试触法
试触法电路图如图 5 所示,先把电压表一端固定在 a 端,另一端先后与 b、c 点试触,当电流表的示数变化明显时,说明电压表内阻分流明显,对电路影响大,即 Rx 与 RV 可比拟,Rx 属于大电阻,电路应当采用内接法;当电压表的示数变化明显时,说明电流表内阻分压明显,对电路影响大,即 Rx 与 RA 可比拟,Rx 属于小电阻,电路应当采用外接法。

发布时间:2022/5/24 上午9:31:31 阅读次数:6748
