第 2 章 第 4 节 科学测量：用单摆测量重力加速度

物理量的测量通常有多种方法。我们已学过用打点计时器或频闪照相来测量重力加速度。下面，我们通过单摆来测量重力加速度的大小。

实验目的

（1）用单摆测量重力加速度。

（2）会使用秒表测量时间。

（3）能分析实验误差的来源，并能采用适当方法减小测量误差。

实验器材

长约 1 m 的细线、开有小孔的金属小球、带有铁夹的铁架台、刻度尺、秒表、游标卡尺。

实验原理与设计

单摆做简谐运动时，由周期公式 T = 2π\(\sqrt {\frac{l}{g}} \)，可得 g = \(\frac{{4{\pi ^2}l}}{{{T^2}}}\)。因此，测出单摆摆长和振动周期，便可计算出当地的重力加速度。

用秒表测量 30 ～ 50 次全振动的时间，计算平均做一次全振动的时间，得到的便是振动周期。

安全警示

按操作规程使用秒表、游标卡尺等器材，轻拿轻放金属小球等，不要随意甩动小球，以免伤人。

实验步骤

（1）取长约 1 m 的细线，细线的一端连接小球，另一端用铁夹固定在铁架台上，让摆球自由下垂，如图 2-21 所示。

（2）用刻度尺测摆线长度 l_线，用游标卡尺测小球的直径 d。测量多次，取平均值，计算摆长 l = l_线 + \(\frac{1}{2}\)。

（3）将小球从平衡位置拉至一个偏角小于 5° 的位置并由静止释放，使其在竖直面内振动。待振动稳定后，从小球经过平衡位置时开始用秒表计时，测量 N 次全振动的时间 t，则周期 T = \(\frac{t}{n}\)。如此重复多次，取平均值。

（4）改变摆长，重复实验多次。

（5）将每次实验得到的 l、T 代入 g = \(\frac{{4{\pi ^2}l}}{{{T^2}}}\) 计算重力加速度，取平均值，即为测得的当地重力加速度。

数据分析

将测量的数据记入你设计的表格中，并分析数据，形成结论。

实验结论

写出实验结论。

讨论

（1）通过哪些方式可使小球的运动更加接近简谐运动？

（2）为什么要从平衡位置开始计时、计数？为什么不用秒表直接测量一次全振动的时间作为周期？除秒表外，测量时间还可选用哪些器材？

（3）你还能用什么方法测量重力加速度？

素养提升

能分析相关事实，提出并准确表述在实验中可能出现的物理问题；能在他人帮助下制订实验方案，能选用实验器材进行实验，获得实验数据，能注意减小实验误差；能分析数据，测得重力加速度的大小；能撰写规范的实验报告，在报告中能呈现设计的实验表格、数据分析过程及实验结论，能反思评估关于重力加速度的不同测量方法。

注意提升实验测量能力与误差分析能力。

——科学探究

物理聊吧

除了用公式法处理数据外，还可用图像法处理数据。图 2-22 是某同学作出的 T²-l 图像，如何从图像中求出重力加速度？请与同学交流你的想法。

科学书屋

秒表

秒表可分为机械秒表和电子秒表。机械秒表有大、小两个表盘（图 2-23），秒针沿大表盘转动，分针沿小表盘转动。通常，秒针转一圈所用的时间为30 s，最小分度为0.1 s。秒针每转过一圈，分针相应转过半格。分针和秒针所指示的时间之和为所测的时间。图中，分针转过半格，即示数为 30 s，秒针示数为 3.4 s，故所测时间为 33.4 s。秒针的转动是通过齿轮传动的，不可能停在两格中间，所以不需要估读。秒表上方的按钮起着控制指针走动和扭紧发条的作用。使用时先扭紧发条，按下按钮，秒表开始计时；再按下按钮，秒表停止计时，进行读数；再按一次，秒表回零，准备下一次计时。

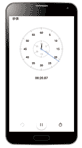
电子秒表采用液晶数字显示时间。通常，按一下START/STOP 按钮，开始自动计时；再按一下，停止计时并显示出所记录的时间；然后按 LAP/RESET 键回零。手机一般也有秒表的计时功能（图 2-24）。

节练习

1．请撰写“用单摆测量重力加速度的大小”的实验报告。注意在报告中呈现设计的实验表格以及数据分析过程和实验结论，讨论重力加速度的不同测量方法的特点。

参考解答：略

2．在“用单摆测量重力加速度的大小”实验中，某同学发现他测出的重力加速度值总是偏小，可能有哪些原因？

参考解答：根据单摆的公式 T = 2π\(\sqrt {\frac{l}{g}} \)，可得 g = \(\frac{{4{\pi ^2}l}}{{{T^2}}}\)；测得的加速度偏小可能是 l 偏小可能是 T 偏大。即把摆线的长当作摆长来计算，没有算上小球的半径，这样 l 偏小，算出来的重力加速度偏小；测出 n 次全振动的时间，误作为 （n − 1） 次全振动的时间进行计算，测得的周期偏大，算出来的重力加速偏小。振动中出现松动，使摆线长度增加了，测得的周期偏大，则测得的 g 值偏小。

3．一位同学用单摆测量重力加速度，他将单摆挂起后，进行了如下操作。请指出下列步骤中遗漏或错误的地方，并加以改正。

（1）测摆长 l：用刻度尺量出摆线的长度。

（2）测周期 T：将小球拉起，由静止释放，在小球某次通过最低点时，按下秒表开始计时，同时将本次通过最低点记为第 1 次；接着一直数到小球第 60 次通过最低点时，按下秒表停止计时；读出这段时间 t，算出单摆的周期 T = \(\frac{t}{60}\)。

（3）将所测得的 l 和 T 代入公式 T = 2π\(\sqrt {\frac{l}{g}} \)，算出 g，将其作为实验结果写入报告中。

参考解答：（1）摆长不等于摆线的长度，所以要用卡尺测出摆球直径 d，摆成 l 等于摆线长与 \(\frac{d}{2}\) 之和。

（2）一个周期内两次通过最低点，按秒表开始计时，并计数为 1，直到摆球第 60 次通过最低点时停止计时，所以共有 29.5 次全振动。所以 T = \(\frac{t}{29.5}\)。

（3）不能将单独一次的实验数据作为最终结果。g 应多次测量，然后取平均值作为实验最后结果。

4．在做“用单摆测量重力加速度的大小”实验时，如果已知小球直径为 1.80 cm，让刻度尺的0 刻度线对准摆线的悬点， 摆线竖直下垂，下端刻度如图（a）所示，那么单摆的摆长是________m。若测定 40 次全振动的时间如图（b）中秒表所示，则秒表读数是 ________ s，单摆的振动周期是 ________ s。由此得到的重力加速度 g =________m/s²。

参考解答：0.8730，75.2，1.88，9.74

5．某同学在做“用单摆测量重力加速度的大小”实验时，测量了 5 种不同摆长情况下单摆的振动周期，记录数据如下：

（1）根据表中数据画出 T² - l 图像；

（2）求此图像的斜率；

（3）由此图像求重力加速度。

参考解答：（1）图略。

（2）k = 4.03

（3）g ≈ 9.79 m/s²

6．北京和广州的两位同学，分别探究单摆的周期 T 与摆长 l 的关系，通过网络交流绘制了 T² - l 图像，如图（a）所示。

（1）北京的同学所测实验结果可能对应的图像是 A 和 B 中的哪一个？请说明理由。

（2）广州的同学还绘制了不同摆长的单摆的振动图像，如图（b）所示。由图可知两单摆摆长之比 l_a∶l_b 为多少？

参考解答：（1）由公式 T = 2π\(\sqrt {\frac{l}{g}} \)，因为在地球表面纬度越大重力加速度越大，所以北京重力加速度大于海南重力加速度，所以单摆在北京的周期应该小于海南，北京的同学所测实验结果对应的是图线 B。

（2）l_a∶l_b = 4∶9

发布时间：2022/5/9 下午8:07:34  阅读次数：3996