第 1 章 第 1 节 动量和动量定理

碰撞现象在生活中司空见惯。通常，鸡蛋从高处落到坚硬的盘子里会破，但若落在较厚的软垫上还会破吗（图 1-1）？本节我们学习了动量、冲量和动量定理后，便能解释这类现象。

1．动量

在游乐场开碰碰车（图 1-2），当运动的车去碰静止的车，若运动的车的总质量越大、车速越大，那么静止的那辆车会被撞得越远。可见，碰撞产生的效果与碰撞物体的质量和速度都有关。

迷你实验室

观察小球的碰撞

如图 1-3 所示，将质量相等的两个钢球 A、B 并排悬挂起来。把球 A 分别拉到不同高度释放，去碰撞静止的球 B，观察球 B 每次上升的最大高度。

将球 A 换成质量不同的钢球，分别拉到同一高度释放，再观察球 B 每次上升的最大高度。

由实验可知，从不同高度释放同一钢球，高度越高，被碰球上升越高；从同样高度释放质量不同的钢球，质量越大，被碰球上升越高。由此可见，对同一被碰球，其上升的高度与碰撞球的质量和碰前速度都有关。

人们在研究碰撞这类问题时，为了更好地说明问题，引入了一个与质量和速度都有关的物理量—动量。物理学中，把物体质量与速度的乘积称为物体的动量（momentum），通常用字母 p 表示。

\[p = mv\]

动量的单位由质量的单位和速度的单位共同决定。在国际单位制中，动量的单位是千克米每秒，符号为 kg·m/s。动量是矢量，它的方向与物体速度的方向相同。

物体在运动过程中，当速度的大小或方向变化时，动量会发生变化。物体动量的变化量 Δp 等于物体的末动量 p₂ 与初动量 p₁ 的矢量差，即 Δp = p₂ − p₁。动量的变化量也是矢量。

例题

如图 1-4 所示，一质量为 58 g 的网球以 30 m/s 的速率水平向右飞行，被球拍击打后，又以 30 m/s 的速率水平返回。被球拍击打前后，球的动量分别是多少？球的动量的变化量是多少？

分析

根据动量定义可求被击打前后网球的动量。由于球在被击打前后的动量在同一直线上，可利用同一直线上的矢量运算法则计算动量的变化量。

解

选定水平向右为正方向。由题意可知，m = 58 g = 0.058 kg，v₁ = 30 m/s，v₂ = −30 m/s。

击打前，球的动量

p₁ = mv₁ = 0.058×30 kg·m/s = 1.74 kg·m/s

球被击打前的动量大小为 1.74 kg·m/s ，方向水平向右。

击打后，球的动量

p₂ = mv₂ = 0.058×（−30 ）kg·m/s = −1.74 kg·m/s

球被击打后的动量大小为 1.74 kg·m/s ，方向水平向左。球被击打前后动量的变化量

Δp = p₂ − p₁ =（−1.74 − 1.74）kg·m/s = −3.48 kg·m/s

球被击打前后动量的变化量大小为 3.48 kg·m/s，方向水平向左。

讨论

球被击打前后，虽然动量的大小没有变化，但动量的方向发生了改变，因此动量发生了变化。求得动量的变化量为负值，表示其方向与选定的正方向相反。

策略提炼

动量与动量的变化量都是矢量。如果动量的方向都在同一直线上，在选定一个正方向后，已知矢量的方向用正、负号表示，动量及动量的变化量的运算就变为代数运算。

迁移

对同一条直线上的矢量运算，正方向的选定是任意的。例题中，若选定水平向左为正方向，结果又如何？请计算并与例题的结果进行比较。

2．动量定理

由以上例题可知，网球运动员击球时，球拍的作用力使球的动量发生了变化。在生产生活中，物体动量发生变化的现象随处可见。物体动量的变化与哪些因素有关呢？

对于一个质量不变的物体，速度的变化导致动量的变化，而物体速度的变化除了与物体受力情况有关外，还与力作用于物体的时间有关。例如，火车启动时，若牵引力小，则需要较长的时间才能达到正常的行驶速度；若牵引力大，则只需较短的时间便可达到正常的行驶速度。下面我们来推导，在恒力作用的情况下，物体动量的变化量与作用力和时间的定量关系。

设一质量为 m 的物体，初速度为 v₁，初动量 p₁ = mv₁。在合外力 F 的作用下，经过一段时间 t，速度变为 v₂，末动量 p₂ = mv₂（图 1-5）。物体的加速度

\[a = \frac{{{v_2} - {v_1}}}{t}\]

代入牛顿第二定律得

\[F = ma = m\frac{{{v_2} - {v_1}}}{t}\]

变形得

\[Ft = m{v_2} - m{v_1}\]

物体动量的变化量既与受到的合外力有关，又与该力的作用时间有关。合外力越大、作用时间越长， 物体动量的变化量就越大。可见，Ft 这个量反映了力对时间的积累效应。物理学中，把力和力的作用时间的乘积称为这个力的冲量（impulse），通常用符号 I 表示。

\[I = Ft\]

冲量也是矢量，它的方向与力的方向相同。在国际单位制中，冲量的单位是牛·秒，符号为 N·s。

由此，Ft = mv₂ − mv₁ 还可表示为

\[I = m{v_2} - m{v_1}\]

由上式可知，物体在一过程中所受合外力的冲量等于该物体在此过程中动量的变化量。这称为动量定理（theorem of momentum）。

由动量定理可得

\[F = \frac{{m({v_2} - {v_1})}}{t}\]

该式表明，作用在物体上的合外力等于物体动量的变化率，这实际上是牛顿第二定律的另一种表述。可进一步证明，在变力作用下，动量定理仍然成立。

例题

一个质量为 60 kg 的男孩从高处跳下，以 5 m/s 的速度竖直落地。取重力加速度 g = 10 m/s²。

（1）若男孩落地时屈膝（图 1-6），用了 1 s 停下来，则落地时地面对他的平均作用力是多大？

（2）若男孩落地时没有屈膝，只用了 0.1 s 就停下来，则落地时地面对他的平均作用力又是多大？

分析

男孩刚触地时动量方向竖直向下，一段时间内减小到 0，这一过程中地面对脚的作用力是变力。根据动量定理可求出落地时地面对他的平均作用力。

解

男孩落地时的受力分析如图 1-7 所示，选定竖直向上为正方向。设地面对他的平均作用力为 \({\bar F}\)，由题意可知，m = 60 kg，v₁ = − 5 m/s，v₂ = 0。

（1）男孩从触地到速度减为 0，经历的时间 t₁ = 1 s。由动量定理得

（\({\bar F}\)₁ − mg）t₁ = mv₂ − mv₁

\({\bar F}\)₁ = −\(\frac{{m{v_1}}}{{{t_1}}}\) + mg

=（\(\frac{{60 \times 5}}{1}\) + 60×10）N = 9.0×10² N

方向竖直向上。

（2）男孩从触地到速度减为 0，经历的时间 t₂ = 0.1 s。同理可得，地面对他的平均作用力

\({\bar F}\)₂ = −\(\frac{{m{v_1}}}{{{t_2}}}\)  + mg =（\(\frac{{60 \times 5}}{0.1}\) + 60×10）N = 3.6×10³ N

方向竖直向上。

讨论

两种落地方式中，动量的变化量相同，但所经历时间不同。作用时间越短，地面对人的平均作用力越大。因此，人从高处跳下时，为避免受伤，要尽量延长触地后的缓冲时间，以减小地面对人的作用力。由此，你能解释鸡蛋从高处落到软垫上不容易破的原因吗？

策略提炼

在碰撞这类问题中，相互作用力会发生变化，可根据动量定理计算变力的平均值。

运用动量定理分析问题时，要注意明确研究对象和过程，正确分析受力和运动的初、末状态；注意动量定理是矢量式，需根据矢量运算法则建立方程。

迁移

在碰撞这类问题中，由于相互作用时间极短，相互作用力会很大，通常可忽略其他较小的力而使问题简化。例如，在前面击打网球的例题中，若球与球拍的接触时间为 0.01 s，球受到球拍击打的平均作用力是多大？

科学书屋

关于“运动的量度”的争论

关于“运动的量度”，历史上有两种不同的观点。1644 年，笛卡儿提出“运动不灭原理”：物质的运动有一个固定的量，这个量从来不增加也不减少，并把物体的质量和速度的乘积（mv）作为物体的“运动量”的量度。而莱布尼茨（G. Leibniz，1646—1716）认为，活力（mv²）才是物体的“运动量”的量度。这场著名的争论延续了半个世纪之久。1743 年，法国力学家达朗贝尔（J. le R. D’Alembert，1717—1783）对这场争论给出了“判决”：两种量度是同样有效的。达朗贝尔的“判决”模糊谈到了：动量的变化和力的作用时间有关，活力的变化和力的作用距离有关。直到一百多年后，人们建立了能量转化与守恒定律，才进一步认识到这两种量度的区别。

对某一问题的认识有时会存在不同的观点，科学争论往往可帮助人们从多维的思想方法中得到启迪，从而更深刻、更全面地理解和认识问题。

3．碰撞与缓冲的实例分析

由动量定理可见，物体间的相互作用力与物体动量的变化和作用时间有关。既可通过增大物体动量变化量、缩短相互作用时间来增大相互作用力，也可通过减小物体动量变化量、延长相互作用时间来减小相互作用力。例如，冲床冲压工件时，由于冲头动量变化大且冲头与工件的碰撞时间短，在冲头与工件间会产生很大的作用力。冲压工件就是利用了这种作用力。修路、建房时常用打夯机。打夯时（图 1-8），打夯机将夯锤提到一定高度释放，通过夯锤撞击地面夯实地基。夯锤质量越大、提升高度越高、与地面的撞击时间越短，夯实地面就越有效。为保证驾乘人员的安全，有的汽车在相关部位安装了安全气囊，利用气囊的形变来延长力的作用时间，减轻因剧烈碰撞而造成的对车内人员的伤害（图 1-9）。

DIS实验室

验证动量定理

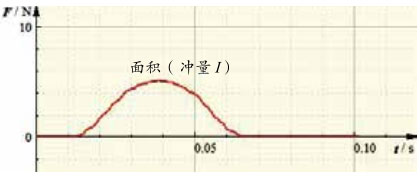
我们可用 DIS 实验装置验证在变力作用下的动量定理。如图 1-10 所示，将力传感器、光电传感器接入电路，将遮光片的宽度和小车质量输入计算机。推动小车使其与力传感器发生碰撞，通过碰撞中相互作用力随时间变化的图像（图 1-11）可得出小车受到的力的冲量，再由光电传感器测量的时间等可得到小车动量的变化量。比较小车受到的力的冲量和动量变化量，验证动量定理。

节练习

1．运输易碎器件时，经常在包装箱中填充泡沫塑料；为营救高空坠落者，常会在坠落者下方放置气垫。请解释这样做的理由。

参考解答：这样做是为了增加作用时间，从而减少对器件或坠落者的作用力，避免或减轻造成的伤害。

2．若质量为 m 的物体在某时刻的动量大小为 p，动能为 E_k，试证明：p² = 2mE_k。

参考解答：p² = （mv）² = 2m×\(\frac{1}{2}\)mv² = 2mE_k，即 p² = 2mE_k。

3．在某轿车的撞击实验中，有一质量为 60 kg 的人体模型坐在驾驶位置，轿车以 108 km/h 的速度撞到坚固的墙，假设该模型与车皆在 0.2 s 内停下。

（1）此模型在水平方向所受力的平均值为多少？

（2）有人认为，在类似的事故中，如果人用双手抵住方向盘，便可止住突然向前倾倒的身体。请对上述看法作出评价，并说出你的依据。

参考解答：（1）此模型在水平方向所受力的平均值为9 000 N，方向与轿车出速度的方向相反。上述看法是不正确的。

（2）9 000 N 约等于质量为 900 kg 的物体的重力，这近似相当于 15 个人同时站在人的双手上。显然，人的双手无法承受如此巨大的作用力。故上述看法是不正确的。

4．一小球从某高处以 10 m/s 的速度竖直向上抛出，落到地面时速度大小为 20 m/s。求小球在空中的运动时间。（取重力加速度 g = 10 m/s²，不计空气阻力）

参考解答：t = 3 s

5．高空作业必须系安全带。如果质量为 m 的高空作业人员不慎跌落，从开始跌落到安全带对人刚产生作用力的过程中，人下落的距离为 h（可视为自由落体运动）。此后经历时间 t，安全带达到最大伸长量，若在此过程中安全带的作用力始终竖直向上，则该段时间内安全带对人的平均作用力大小为多少？请提出关于安全带设计的建议。

参考解答：F = mg + \(\frac{{m\sqrt {2gh} }}{t}\)

安全带设计的建议：

（1）适当增大安全带所能承受的最大拉力；

（2）选用合适材料，延长人与安全带的作用时间。

（其他合理建议均可）

6．一质量为 1 kg 的物体在外力的作用下从静止开始做直线运动，其所受的合外力随时间变化的图像如图所示。求物体分别在 2 s 末、6 s 末和 9 s 末的速度。

参考解答：v₁ = 4 m/s，v₂ = 0，v₃ = − 2 m/s

*7．现代切割技术常用的一种“水刀”如图所示。它将水从高压水枪中高速射出，形成很细的水束，用来切割钢板等物体。已知水束的横截面积为 S，速度为 v，并垂直射向钢板，若水射上钢板后的速度视为 0，水的密度为 ρ，求水对钢板的平均冲击力。

参考解答：F = ρSv²

本套选择性必修教材的习题，对应不同的学业质量水平，其中题号标有“*”的习题有一定难度，可根据具体情况选做。

发布时间：2022/5/1 下午7:50:13  阅读次数：4598