第四章 运动和力的关系 复习与提高
A 组
1.在公路上,一辆汽车以较大的速度行驶,紧急刹车制动时间大于以较小速度行驶时的制动时间。这是因为速度越大,车的惯性越大吗?如果不是,上述现象该如何解释?
2.质量为 0.5 kg 的物体,受到方向相反的两个力作用,获得 3 m/s2 的加速度。若将其中一个力加倍,物体的加速度大小变为 8 m/s2,求另一个力的大小。
3.以 6 m/s 的速度匀速上升的气球,当升到离地面 14.5 m 高时,从气球上落下一小球,小球的质量为 0.5 kg,假设小球在运动过程中所受的阻力大小总等于 1 N。小球经多长时间到达地面?g 取 10 m/s2。
4.图 4–1 是采用动力学方法测量空间站质量的原理图。若已知飞船质量为 3.0×103 kg,其推进器的平均推力 F 为 900 N,在飞船与空间站对接后,推进器工作 5 s 内,测出飞船和空间站的速度变化是 0.05 m/s,求空间站的质量。
5.在解答一道已知量完全由字母表达结果的计算题时,一个同学解得某物体位移 x = \(\frac{{F}}{2m}\)(t1+t2),请你用单位制的知识检查,说明这一结果是否可能正确。
6.如图 4–2,在倾角 37° 足够长的斜面上有一个质量为 1 kg 的物体,物体与斜面之间的动摩擦因数为 0.3。物体在拉力 F 的作用下由静止开始运动,F 的大小为 10 N,方向沿斜面向上。加速一段时间后撤去 F,让物体在斜面上运动。
g 取 10 m/s2。
(1)物体从静止开始一共经历了哪几个匀变速直线运动过程?
(2)这几个匀变速直线运动的加速度的大小和方向如何?
7.某小组通过测量两辆小车在相同时间内通过的位移来比较它们的加速度,进而探究加速度与力的关系,实验装置如图 4–3 所示。将轨道分上下双层排列,两小车尾部的刹车线由后面的刹车系统同时控制,能使小车同时立即停下来。通过改变槽码盘中的槽码来改变拉力的大小。
(1)通过比较两小车的位移来比较两小车的加速度大小,你认为可行吗?请说明理由。
(2)已知两小车质量均为 500 g,实验数据如表 1 中所示。
分析表中数据,你能得到什么结论?说出你的分析过程。
| 实验次数 | 小车 | 拉力 F/N | 位移 x/cm |
| 1 | 甲 | 0.1 | 22.3 |
| 乙 | 0.2 | 43.5 | |
| 2 | 甲 | 0.2 | 29.0 |
| 乙 | 0.3 | 43.0 | |
| 3 | 甲 | 0.3 | 41.0 |
| 乙 | 0.4 | 55.4 |
(3)如果还要利用上述装置进行“探究加速度与质量的关系”实验,应该怎样调整实验条件?
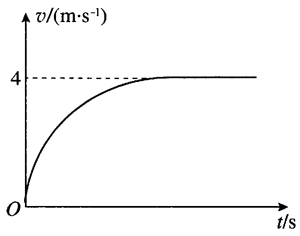
8.某同学为研究雨滴下落的规律查阅资料,了解到:较大的雨滴是从大约 1 000 m 的高空形成并下落的,到达地面的速度大约为 4 m/s。根据以上信息,可以把雨滴的运动模型看成是 1 000 m 高空的物体在有空气阻力的空间中由静止开始下落的运动,雨滴所受空气阻力随速度的增大而增大。请你分析雨滴下落的运动过程,描述雨滴下落过程中速度和加速度的变化,并
定性作出雨滴下落的 v–t 图像。
9.某同学制作了一个“竖直加速度测量仪”,可以用来测量竖直上下电梯运行时的加速度,其构造如图 4–4 所示。把一根轻弹簧上端固定在小木板上,下端悬吊 0.9 N 重物时,弹簧下端的指针指木板上刻度为 C 的位置,把悬吊 1.0 N 重物时指针位置的刻度标记为 0,以后该重物就固定在弹簧上,和小木板上的刻度构成了一个“竖直加速度测量仪”。
(1)请在图中除 0 以外
的 6 根长刻度线旁,标注加
速度的大小,示数的单位用
m/s2 表示,加速度的方向
向上为正、向下为负。
说明这样标注的原理。
(2)仿照以上装置,
设计一个“水平加速度
测量仪”。要求:画出它
的装置图;说明它的构造;
介绍加速度刻度的标注原理。
g 取 10 m/s2。
B 组
1.如图 4–5,两个质量相同的小球 A 和 B 之间用轻弹簧连接,然后用细绳悬挂起来,剪断细绳的瞬间,A 球和 B 球的加速度分别是多少?
2.如图 4–6,质量为 0.5 kg 的物块 A 放在一个纵剖面为矩形的静止木箱内,A 和木箱水平底面之间的动摩擦因数为 0.3。A 的右边被一根轻弹簧用 1.2 N 的水平拉力向右拉着而保持静止。现在要使弹簧能拉动物块 A 相对木箱底面向右
移动。设最大静摩擦力等于滑动摩擦力,g 取 10 m/s2。
(1)如果让木箱在竖直方向上运动,其加速度应满足什么条件?
(2)如果让木箱在水平方向上运动,其加速度应满足什么条件?
3.为了安全,在公路上行驶的汽车之间应保持必要的距离。如果一辆汽车在高速公路上
行驶的速度为 120 km/h,通常人的反应时间为 0.3 ~ 0.6 s,结合表 2 提供的资料,请通过计算说明不同路况下的安全距离。g 取 10 m/s2。
| 路面 | 动摩擦因数 |
| 干沥青与混凝土路面 | 0.7 ~ 0.8 |
| 干碎石路面 | 0.6 ~ 0.7 |
| 湿沥青与混凝土路面 | 0.32 ~ 0.4 |
4.在民航机场和火车站可以看到用于对行李进行安全检查的水平传送带。旅客把行李放到传送带上时,传送带对行李的滑动摩擦力使行李开始运动,随后它们保持相对静止,行李随传送带一起前进。若传送带匀速前进的速度 v 为 0.25 m/s,某木箱与传送带之间的动摩擦因数 μ 为 0.4,g 取 10 m/s2。问:该木箱放在传送带上后,传送带上将留下一段多长的摩擦痕迹?

5.某人想测量地铁启动过程中的加速度,他把一根细绳的下端绑着一支圆珠笔,细绳的上端用电工胶布临时固定在地铁的竖直扶手上。在地铁启动后的某段加速过程中,细绳偏离了竖直方向,他用手机拍摄了当时情景的照片(图 4–7),拍摄方向跟地铁前进方向垂直。根据这张照片估算此时地铁的加速度是多少?加速
度方向指向照片的哪个方向?请写明测量步骤、数据、计算过程和结果。
6.如图 4–8,A、B 两个物体相互接触,但并不黏合,放置在水平面上,水平面与物体间的摩擦力可忽略,两物体的质量 mA 为 4 kg,mB 为 6 kg。从 t = 0 开始,推力 FA 和拉力 FB 分别作用于 A、B 上,FA、FB 随时间的变化规律为
FA=(8-2t)(N)
FB=(2+2t)(N)
问:8 s 内物体 B 运动的加速度如何变化?
7.如图 4–9,质量为 2.5 kg 的一只长方体形空铁箱在水平拉力 F 作用下沿水平面向右匀加速运动,铁箱与水平面间的动摩擦因数 μ1 为 0.3。这时铁箱内一个质量为 0.5 kg 的木块恰好能静止在后壁上。木块与铁箱内壁间的动摩擦因数 μ2 为 0.25。设最大静摩擦力等于滑动摩擦力,g 取 10 m/s2。
(1)求木块对铁箱压力的大小 ;
(2)求水平拉力 F 的大小;
(3)减小拉力 F,经过一段时间,木块沿铁箱左侧壁落到底部且不反弹,当铁箱的速度为 6 m/s 时撤去拉力,又经 1 s 时间木块从左侧到达右侧,则此时木块相对铁箱运动的距离是多少?
“复习与提高”参考答案与提示
习题设计力图渗透高中物理核心素养:理解所学的物理概念和规律及其相互关系,巩固正确的运动和相互作用的观念,能解释自然现象,解决实际问题,如 A1 题解释速度大的汽车制动时间长,A8 题描述雨滴的运动,B3 题计算汽车的安全距离,B4 题计算物体在水平传送带上的划痕长度;学习模型建构,能在熟悉的问题情境中根据需要选用恰当的模型解决简单的物理问题,将实际问题中的对象和过程转换成所学的物理模型,如 A3 题分析匀速上升的气球上落下小球的运动, B1 题求与弹簧相连物体的瞬时加速度,B5 题测量列车启动阶段的加速度;培养科学推理能力,能对常见的物理问题进行分析,通过推理,获得结论并作出解释,如 A2、A6、B2、B4 等题;进行科学论证,恰当使用证据证明物理结论,如A5 题用单位制检查结果;培养质疑创新能力,能对已有结论提出有依据的质疑,采用不同方式分析解决物理问题,如 B6、B7 等题;进行科学探究,能制订科学探究方案,选用合适的器材获得数据,能分析数据,发现其中规律,形成合理的结论,用已有的物理知识进行解释,如 A7 题探究加速度与力、质量的关系、A9 题探究竖直加速度测量仪的原理并尝试设计水平如速度测量仪;培养科学态度与责任,如 A4、B3 等题。
A 组
1.设汽车的运动方向为正方向。汽车在紧急刹车制动的过程中,可以认为汽车所受阻力的大小 Ff 不变,根据牛顿第二定律有 a = \(\frac{{ - {F_f}}}{m}\),车制动的加速度不变;已知末速度为 0,根据匀变速直线运动规律有 Δt = \(\frac{{0 - {v_0}}}{a}\)) = \(\frac{{m{v_0}}}{F}\),若初速度 v0 越大,则制动时间 Δt 越大。
提示:学生在作答时一般会遇到两个思维障碍:第一,不能将汽车紧急刹车制动过程抽象为末速度为 0 的匀减速直线运动,无法正确选择公式 Δt = \(\frac{{0 - {v_0}}}{a}\)) 进行分析。第二,认为两种情况下汽车受到的阻力不同。实际上,汽车在紧急刹车制动的过程中,空气阻力与制动相比可以忽略不计,汽车受到的阻力可以认为相同。
2.1 N 或 7 N
提示:设物体受到的两个水平力分别为 F1、F2,且 F1 > F2,根据牛顿第二定律有
F1 – F2 = ma1 ①
依题意,若将其中一个力加倍,有两种情况:
(1)若将 F1 加倍,则求 F2 的大小,根据牛顿第二定律有
2F1 – F2 = ma2 ②
联立①②解得 F2 = m(a2 − 2a1)= 0.5×(8 − 2×3)N = 1 N。
(2)若将 F2 加倍,则求 F1 的大小,根据牛顿第二定律有
2F2 – F1 = ma2 ③
联立①③解得 F1 = m(a2 + 2a1)= 0.5×(8 + 2×3)N =7 N。
3.2.5 s
提示:理解物体的运动是由物体的初始状态和受力情况确定的,学会将题设条件转化为“小球在离地面 14.5 m 高时,有向上的初速度 6 m/s”。此后,把小球的运动分为向上的匀减速运动和向下的匀加速运动两个阶段处理。
小球脱离气球后匀减速上升,设加速度大小为 a1,则 mg + Ff = ma1。将 Ff = 1 N、m = 0.5 kg、g = 10 m/s2 代入解得 a1 = 12 m/s2。小球匀减速上升的时间 t1 = \(\frac{{0 - {v_0}}}{{ - {a_1}}}\) = \(\frac{1}{2}\) s = 0.5 s。小球匀减速上升的高度 h1 = \(\frac{{0 + {v_0}}}{2}\)t1 = \(\frac{6}{2}\)×0.5 m = 1.5 m。
设小球之后匀加速下降的加速度大小为 a2,则 mg – Ff = ma2。代入数据解得 a2 = 8 m/s2。设小球匀加速下落的时间为 t2,则小球匀加速下落的高度 h0 + h1 = \(\frac{1}{2}\)a2t22。代入数据解得 t2 = 2 s。
故小球脱离气球后,到达地面需要的时间 t = t1 + t2 = 2.5 s。
4.8.7×104 kg
提示:设空间站的履量为 m1、飞船的质量为 m2,根据牛顿第二定律有 F =(m1 + m2)a。又根据加速度定义式有 a = \(\frac{{\Delta v}}{{\Delta t}}\) = \(\frac{0.05}{5}\) m/s2 = 0.01 m/s2。代入数据得 m1 = 8.7×104 kg。
5.在力学单位制中,力 F 的单位是 N,质量 m 的单位是 kg,时间 t 的单位是 s,题中表达式右边的单位换算为 1 \(\frac{{\rm{N}}}{{{\rm{kg}}}}\)·s = 1 \(\frac{{{\rm{kg}} \cdot {\rm{m}} \cdot {{\rm{s}}^{{\rm{ - 2}}}}}}{{{\rm{kg}}}}\)·s = 1 m·s−1。m·s−1 是速度的单位,不是位移 x 的单位,故题中结果错误。
6.(1)在拉力 F 的作用下,物体沿斜面向上先做匀加速直线运动,后做匀减速直线运动,直至速度减为 0。然后沿斜面向下做匀加速直线运动,直至滑离斜面。
(2)物体沿斜面向上做匀加速直线运动,设加速度为 a1,根据牛顿第二定律有 F − (mgsin37° + μmgcos37°) = ma2。代入数据解得 a1 = 1.6 m/s2,方向沿斜面向上。
撤去 F 后,物体沿斜面向上做匀减速直线运动,设加速度为 a2,根据牛顿第二定律有 −(mgsin37° + μmgcos37°) = ma2。代入数据解得 a2 = − 8.4 m/s2,方向沿斜面向下。
由于 μ < tan37°,物体沿斜面向下做匀加速直线运动,直至滑离斜面。设加速度为 a3,根据牛顿第二定律有 mgsin37° − μmgcos37° = ma3。代入数据解得 a3 = 3.6 m/s2,方向沿斜面向下。
7.(1)两辆小车做初速度为 0 的匀加速直线运动的位移 x = \(\frac{1}{2}\)at12,经过相同的时间 t,有 \(\frac{{{a_1}}}{{{a_2}}}\) = \(\frac{{{x_1}}}{{{x_2}}}\)。所以,通过比较两辆小车的位移来比较加速度的大小,这个方案是可行的。
(2)当小车质量不变时,在实验误差范围内,分析每次实验的数据可知,甲、乙两辆小车的位移之比等于拉力之比,而加速度之比等于位移之比,则加速度之比等于拉力之比,故小车的加速度与拉力成正比。
(3)保持槽码盘中的槽码数量不变,改变小车上所加的配重,并使槽码盘和槽码的质量远小于小车和配重的质量。
8.雨滴下落后,速度增大,因此空气阻力增大,加速度减小,雨滴先做变加速直线运动。当加速度减为 0 时,雨滴受到的重力和空气阻力平衡,以 4 m/s 的速度匀速下落到地面。其 v–t 图像如图所示。
9.标注如图 4–8 所示。

(1)以加速度的方向向上为正,根据牛顿第二定律有 F – mg = ΔF = ma,即 a = ( \(\frac{F}{G}\) − 1)g = \(\frac{{\Delta F}}{G}\)g,式中 G = 1.0 N。
已知 C 在从上往下数的第2根长刻度线处,“O”在第4根长刻度线处。设两根长刻度线之间的距离是缸,弹簧的劲度系数为 k。
若指针指在第2根长刻度线处,即 C 处,则 F = 0.9 N,ΔF2 = 2k·Δx = 0.1 N,所以 a2 = − 1.0 m/s2、kΔx = −0.05 N。
若指针指在第1根长刻度线处,则 ΔF1 = 3k·Δx-= − 0.15 N,a1 = − 1.5 m/s2。
若指针指在第3根长刻度线处,则 ΔF3 = k·Δx-= − 0.05 N,a3 = − 0.5 m/s2。
若指针指在第5根长刻度线处,则 ΔF5 = k·Δx = − 0.05 N,a5 = 0.5 m/s2。
同理,若指针指在第 6、7 根长刻度线处,则加速度分别为 1.0 m/s2,1.5 m/s2。
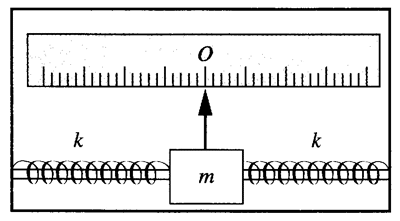
(2)水平加速度测量仪装置构造如图 4–9 所示,在沿水平方向安装的固定光滑杆上套一个质量为 m 的滑块,滑块两侧分别与劲度系数均为 k 的弹簧相连,两弹簧的另一端与固定端相连。滑块原来静止,弹簧处于自然长度,滑块上有指针,可通过标尺测出滑块的位移。若指针向左偏离 O 点的距离为 x,则加速度方向向右,大小为 \(\frac{{2kx}}{m}\)。
B 组
1.0;2g
提示:应用牛顿运动定律求瞬时加速度,理解弹簧的形变是一个渐变过程。在剪断细绳的瞬间,弹簧的弹力不变,而细绳对小球 A 的拉力突变为 0。剪断细绳前,设弹簧弹力为 F,以 B 为研究对象有 F = mg。剪断细绳的瞬间,弹簧弹力 F 不变,所以 aB = 0,aA = \(\frac{{F + mg}}{m}\) = 2g。
2.(1)a1 ≥ 2 m/s2,方向竖直向下;(2)a2 ≥ 0.6 m/s2,方向水平向左
提示:创设木箱在竖直方向和水平方向的两种运动情境,运用牛顿第二定律研究物块 A 能相对木箱向右运动的条件。已知 m = 0.5 kg,μ = 0.3,F = 1.2 N。
(1)设木箱竖直向下的加速度为 a1,,根据牛顿第二定律有 mg – FN = ma1。弹簧能拉动物体,则有 F ≥ μFN。联立解得 a ≥ g − \(\frac{F}{{\mu m}}\) = 2 m/s2,加速度方向竖直向下。
(2)设木箱水平向左的加速度为 a2,弹簧能拉动物体,根据牛顿第二定律有 μmg – F ≤ ma2。解得 a2 ≥ 0.6 m/s2,加速度方向水平向左。
3.(1)若前车突然因撞车等因素而停止,后车驾驶员反应时间为 t0,在 t0 时间内后车匀速运动的位移 x1 = v0t0。路面与轮胎之间的动摩擦因数为 μ,汽车刹车后的加速度大小 a = μg。后车紧急刹车的位移 x2 = \(\frac{{v_0^2}}{{2a}}\)。后车总的位移 x = x1 + x2 = v0t0 + \(\frac{{v_0^2}}{{2a}}\)。
(2)驾驶员最长的反应时间应取 t0 = 0.6 s,雨后路面湿滑的最小动摩擦因数应取 μ = 0.32。汽车行驶的最高速度为 v0 = 120 km/h = 33.3 m/s。则由(1)可知后车行驶的最大距离为 xm = 193.6 m,故 200 m 的行车距离为必要的安全距离。
4.7.8×10−3 m
提示:设木箱与传送带达到柏同速度前的加速度为 a,根据牛顿第二定律有 μmg = ma。解得 a = 4 m/s2。设历时 t 后木箱与传送带速度相同,则 t = \(\frac{v}{a}\) = \(\frac{0.25}{4}\) s = 0.062 5 s。在时间 t 内,木箱的位移 x1 = \(\frac{v}{2}\)t,传送带的位移 x2 = vt。则痕迹长度 Δx = x2 – x1 = \(\frac{v}{2}\)t = 7.8×10−3 m。
5.当圆珠笔与列车相对静止时,圆珠笔的加速度与列车的加速度相同。照片中圆珠笔向右偏,故列车的加速度方向向左。
用量角器测出细线与竖直扶手的夹角 θ = 8°。以圆珠笔为研究对象进行受力分析,根据牛顿第二定律在竖直方向有 FTcosθ – mg = 0,在水平方向有 FTsinθ = ma。解得 a = gtanθ,所以 a = gtanθ = 1.4 m/s2。
6.当 0 ≤ t ≤2 s 时 a1 = 1 m/s2,当 2 s < t < 8 s 时 a2 = \(\frac{{1 + t}}{3}\)(m/s2)。
提示:设两物块在 t1 时刻恰好分离(即相互作用的弹力为 0),此时二者的加速度仍相同,由牛顿第二定律得 \(\frac{{{F_{\rm{A}}}}}{{{m_{\rm{A}}}}}\) = \(\frac{{{F_{\rm{B}}}}}{{{m_{\rm{B}}}}}\),即 \(\frac{{8 - 2{t_1}}}{{{m_{\rm{A}}}}}\) = \(\frac{{2 + 2{t_1}}}{{{m_{\rm{B}}}}}\)。代入数据解得 t1 = 2 s。
则在 0 ~ 2 s 内,两物块以共同的加速度运动。对 A、B 系统,由牛顿第二定律有 FA + FB = (mA + mB)a1。代入数据解得 a1 = 1 m/s2。
2 s 以后,A、B 两物块已分离,对 B 物块,由牛顿第二定律有 FB = mBa2。代入数据得 a2 = \(\frac{{1 + t}}{3}\)(m/s2)。
7.(1)20 N;(2)129 N;(3)0.3 m
提示:第(1)(2)问要求根据解决问题的需要合理选择研究对象。第(3)问要求判断出物体与铁箱不能以共同的加速度做减速运动,能根据物体与铁箱相对运动的方向对物体和铁箱进行正确的受力分析,弄清楚物体与铁箱之间位移的关系。
(1)木块恰好静止在铁箱的后壁上时,木块在竖直方向受力平衡有 μ2FN = m1g。解得铁箱对木块的支持力的大小 FN = 20 N。根据牛顿第三定律,木块对铁箱压力的大小为 FNʹ = 20 N。
(2)木块在水平方向的加速度设为 a,根据牛顿第二定律有 FN = m1a。以整体为研究对象,根据牛顿第二定律有 F – μ1(m1 + m2)g =(m1 + m2)a。联立解得 F = 129 N。
(3)木块落到铁箱底部,撤去拉力后,铁箱和木块均以 v = 6 m/s 的初速度做匀减速直线运动。铁箱受到地面的摩擦力 Ff1 = μ1(m1 + m2)g = 9 N,方向水平向左。铁箱受到木块的摩擦力 Ff2 = μ2m1g = 1.25 N,方向水平向右。
设铁箱的加速度大小为 a1,根据牛顿第二定律有 a1 = \(\frac{{{F_{{\rm{f}}1}} - {F_{{\rm{f2}}}}}}{{{m_2}}}\) = 3.1 m/s2,方向水平向左。
设木块的加速度大小为 a2,根据牛顿第二定律有 a2 = \(\frac{{{F_{{\rm{f2}}}}^\prime }}{{{m_1}}}\) = \(\frac{{{F_{{\rm{f2}}}}}}{{{m_1}}}\) = μ2g = 2.5 m/s2,方向水平向左。
经过 1 s,木块从铁箱的左侧到达右侧,则木块对地位移 s2 = vt − \(\frac{1}{2}\)a2t2。铁箱对地位移 s1 = vt − \(\frac{1}{2}\)a1t2。故铁箱的长度 s = s1 – s2 = \(\frac{1}{2}\)(a2 – a1)t2 = 0.3 m。
发布时间:2022/4/12 下午10:40:59 阅读次数:4599
