第 2 章 第 1 节 静电力做功与电势能

我们知道，在攀岩运动中，若攀岩者上升，则重力做负功；若攀岩者下降，则重力做正功。重力做功的多少与攀岩者的始末位置有关，与攀岩路径无关。那么，电荷在静电力作用下运动，若静电力对电荷做功，与重力做功有无相似之处？本节将学习静电力做功的特点，探究静电力做功与电势能变化之间的关系。

1．静电力做功的特点

如图 2 – 1 所示，在电场强度为 E 的匀强电场中，若将一个带正电的试探电荷 q 沿电场方向从 A 点移动到 B 点，移动距离为 d，试探电荷受到的静电力 F = qE，静电力 F 对试探电荷做功

W₁ = qEd

如果将这个试探电荷从 A 点沿折线 ACB 移动到 B 点，当试探电荷沿直线 AC 移动时，静电力 F 与位移的夹角为 θ，移动距离为 l；当试探电荷沿直线 CB 移动时，静电力 F 与位移的夹角为 90°，移动距离为 l′。那么，静电力 F 对试探电荷做功

W₁ = Flcosθ + Fl′ cos 90° = Fd + 0 = qEd

图 2 – 1 分析静电力做功的示意图

这表明，试探电荷从 A 点沿折线 ACB 移动到 B 点，与直接从 A 点沿直线 AB 移动到B 点相比，静电力做的功是相同的。如果试探电荷沿着任一路径从 A 点移动到 B 点（如图 2-1 中绿色线表示的路径），静电力做的功又等于多少呢？请你尝试证明一下，是否仍然为 qEd。

由以上分析证明可知，在匀强电场中移动试探电荷时，静电力做功与路径无关，与电荷的始末位置有关。可以证明这个结论对于一切静电场都适用。

2．电势能

功是能量转化的量度。在力学中，我们根据重力做功与路径无关的特点，引入了重力势能的概念。重力做的功量度了重力势能的变化。当重力做负功时，物体的重力势能增大；当重力做正功时，物体的重力势能减小。

同样，由于静电力做功与移动路径无关，电荷在电场中也具有势能，这种势能称为电势能（electric potential energy）。与重力做功类似，静电力做功也可以量度电势能的变化。

在图 2-2 中，如果外力克服静电力做功，把正电荷 q 从 B 点移动到 A 点，外力对电荷做的功使其他形式的能转化成电势能储存起来，电荷的电势能增大；如果电荷在静电力的作用下从 A 点移动到 B 点，静电力对电荷做功，储存的电势能就释放出来，电荷的电势能减小，即静电力做的功等于电势能的减小量。用 W_AB 表示电荷从 A 点移动到 B 点过程中静电力所做的功，E_pA 和 E_pB 分别表示电荷在 A 点和 B 点的电势能，那么

W_AB = E_pA − E_pB

也就是说，静电力做功的过程就是电势能与其他形式能量转化的过程。静电力做正功，电势能减小；静电力做负功，电势能增大。

在讨论重力势能时，要先规定物体在某一位置的重力势能为零，然后才能确定物体在其他位置的重力势能。同样，在讨论电势能的时候，也需要先规定电荷在某一位置的电势能为零（零电势能点），然后才能确定电荷在其他位置的电势能。电荷在电场中某点的电势能，等于电荷从该点移动到零电势能点静电力所做的功。在图 2-2 中，如果规定 B 点为零电势能点，在静电力的作用下，正电荷 q 从 A 点移动到 B 点，静电力做功为 qEd，则正电荷 q 在 A 点的电势能为 qEd。

图 2 – 2 静电力做功与电势能变化示意图

显然，选择不同的零电势能点，电荷在电场中同一点的电势能的值是不同的，但电场中两点间的电势能之差却不会因零电势能点的选择不同而发生变化。选择恰当的零电势能点，常可使问题简化。在实际应用中，通常将电荷在大地表面的电势能规定为零，或者将电荷在离场源电荷无穷远处的电势能规定为零。如图 2-3 所示，在正点电荷所产生的电场中，取无穷远处为零电势能点，A、B 两点的电荷 q_A 、q_B 的电势能分别等于将 q_A、q_B 由 A、B 两点沿任意路径移到无穷远处静电力做的功，即 E_pA = W_A∞，E_pB = W_B∞。

图 2 – 3 分析点电荷电场中电势能的示意图

由静电力做功与电势能变化的关系，我们可根据静电力做功确定电势能的变化，也可根据电势能的变化确定静电力做的功。

在同一电场中， 同样从 A 点到 B 点， 正电荷与负电荷对应的电势能的变化是相反的。若以 B 点为零电势能点，正、负电荷在 A 点的电势能不同，这说明电荷在电场中的电势能与电荷有关。请比较电势能与重力势能特点的异同。

方法点拨

我们通过与重力势能的类比，引入了电势能的概念。类比是由两个对象的某些相同或相似的性质，推断它们的其他性质有可能相同或相似的推理方法。研究物理问题常采用类比的方法。

例题

如图 2-4 所示，两块平行金属板间距离为 4 cm，电场强度为 5×10⁵ N/C。一电子沿电场线从正极板运动到负极板时，静电力做了多少功？它的电势能怎样变化？若规定负极板为零电势能点，电子在正极板的电势能多大？（电子电荷量的大小为 1.60×10⁻¹⁹ C）

分析

由已知条件可确定在电子运动过程中静电力做的功，再根据静电力做功与电荷电势能变化的关系即可得出电势能的变化情况。

解

已知 E = 5×10⁵ N/C，q = 1.60×10⁻¹⁹ C，d = 0.04 m。电子从正极板运动到负极板过程中，所受静电力方向与位移方向相反，静电力做的功

W = qEd cos 180°

= − 1.60×10⁻¹⁹×5×10⁵×0.04 J

= − 3.2×10⁻¹⁵ J

所以，电子的电势能增大了 3.2×10⁻¹⁵ J。

若规定负极板为零电势能点，电子在正极板具有的电势能

E_p = W = − 3.2×10⁻¹⁵ J

负号表示电子在正极板的电势能比在负极板的电势能小。

讨论

电子从正极板运动到负极板过程中电势能增加，增加的电势能是由什么能量转化而来的？

策略提炼

静电力做功与电势能变化的关系，和重力做功与重力势能变化的关系类似。不管是正电荷还是负电荷，只要静电力对电荷做正功，电荷的电势能就减小；静电力对电荷做负功，电荷的电势能就增大。

迁移

若把例题中的电子换为质子，其他条件不变，质子的电势能怎样变化？若仍以负极板为零电势能点，质子在正极板具有的电势能多大？（质子的电荷量为 1.60×10⁻¹⁹ C）

解答：电势能减小了 3.2×10⁻¹⁵ J，E_p = 3.2×10⁻¹⁵ J

节练习

1．如图所示，在电场强度为 E 的匀强电场中，A、B 两点相距 l，连线 AB 与电场强度方向的夹角为 θ。将一电荷量为 q 的正电荷分别沿直线 AB、折线 ACB、曲线 ADB 从 A 点移动到 B 点，静电力各做了多少功？

参考解答：W_AB = W_ACB = W_ADB = Eqlcosθ

2．某种静电矿料分选器原理如图所示，带电矿粉经漏斗落入水平匀强电场后，分落在收集板中央的两侧。下列关于矿粉分离的过程表述正确的是

A．带正电的矿粉落在右侧               B．静电力对矿粉做正功

C．带负电的矿粉的电势能变大        D．带正电的矿粉的电势能变小

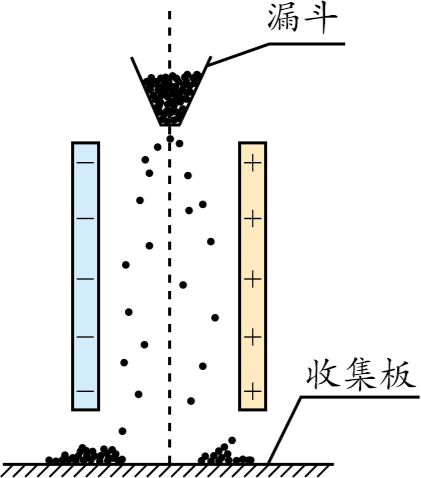
参考解答：BD

3．在静电场中，将一电子从 A 点移动到 B 点，静电力做正功，则

A．电场强度的方向一定是由 A 点指向 B 点

B．电场强度的方向一定是由 B 点指向 A 点

C．电子在 A 点的电势能一定比在 B 点的大

D．电子在 B 点的电势能一定比在 A 点的大

参考解答：C

4．如图所示，静电喷涂时，喷枪喷出的涂料微粒带负电，被喷工件带正电，微粒在静电力作用下向工件运动，最后吸附在工件表面。微粒在向工件靠近的过程中，假设只受静电力作用，那么

A．动能越来越小                      B．动能越来越大

C．克服静电力做功                   D．电势能逐渐减小

参考解答：BD

5．一电荷量为 − 3×10⁻⁶ C 的点电荷，从电场中的 A 点移动到 B 点，克服静电力做功 6×10⁻⁴ J，从 B 点移动到 C 点静电力做功 9×10⁻⁴ J。

（1）若以 B 点为零电势能点，电荷在 A 点的电势能为多少？

（2）若以 C 点为零电势能点，电荷在 A 点的电势能为多少？

参考解答：（1）E_pA = − 6×10⁻⁴ J

（2）E_pA = 3×10⁻⁴ J

6．如图所示，在电场强度为 4×10⁵ N/C 的匀强电场中，将一个电子从 A 点移动到 B 点。已知 A、B 间的距离为 20 cm，连线 AB 与电场线方向成 30° 角，请补充条件，求出电子电势能的变化。

参考解答：可补充条件：电子电荷量为 1.6×10⁻¹⁹ C。ΔE_p = 1.1×10⁻¹⁴ J。

发布时间：2022/4/11 下午1:17:34  阅读次数：3873