第二章 匀变速直线运动的研究 复习与提高

学生运用匀变速直线运动规律分析解决自行车减速、汽车追及、汽车过 ETC 通道、低空跳伞等实际问题。在对实际问题进行推理和分析的过程中，要求学生建构模型，用图像和公式描述匀变速直线运动的规律，用表格、图像、公式处理数据，通过论证得出结论，使学生能在新的情境中灵活运用匀变速直线运动规律，用数学方法解决物理问题，获得正确结论。

A 组

1．自行车无动力滑行的初速度为 v₀ = 4 m/s，末速度为 0，加速度为 a = − 0.2 m/s²，当自行车停止时，滑行位移 x = $\frac{0-v_0^2}{2a}$，代入数据得 x = 40 m > 30 m。可见，自行车仅靠滑行不能停在停车线前。

提示：在自行车减速停止的情境中，要注意加速度的方向与汽车初速度方向相反，解答中的负号就反映了加速度方向。

 

2．20 m

提示：已知 v₀ = 5 m/s，a = − 0.4 m/s²，t = 5 s。则第5 s末的速度为 v = v₀ + at = 5 m/s－0.4×5 m/s = 3 m/s > 0。所以，自行车在斜坡上通过的距离 x = $\frac{v_0+v}{2}$t，代入数据得 x = 20 m。

用匀变速直线运动的速度与时间的关系式和平均速度公式求位移，要注意加速度取负值，要检验结果是否合理，经过判断 5 s 的末速度大于 0。也可以用位移与时间的关系式求自行车在斜坡上通过的距离 x = v₀t + $\frac{1}{2}$at² = 20 m。

 

3．（1）45 m；（2）10 m/s；（3）25 m

提示：（1）钢球下落的高度 h = $\frac{v_3^2}{2g}$，代入数据得 h = 45 m。

（2）钢球在第 2 s 末的速度 v₂ = gt₂ = 20 m/s。故在前 2 s 内的平均速度 v = $\frac{v_2}{2}$ = 10 m/s。

（3）钢球落地时间 t₃ = $\frac{v_3}{g}$ = 3 s，在最后 1 s 内下落的高度 Δh = $\frac{1}{2}$gt₃² − $\frac{1}{2}$g(t₃ − 1)²，代入数据得 Δh = 25 m。

 

4．（1）0.605；0.810；0.996；1.176；1.390；（2）1.94 m/s²

 

提示：（1）相邻计数点间的时间间隔 T = 5×0.02 s = 0.10 s，则 v_A = $\frac{x_{OB}}{2T}$ = 0.605 m/s，v_B = $\frac{x_{AC}}{2T}$ = 0.810 m/s，v_C = $\frac{x_{BD}}{2T}$ = 0.996 m/s，v_D = $\frac{x_{CE}}{2T}$ = 1.176 m/s，v_E = $\frac{x_{DF}}{2T}$ = 1.390 m/s。

（2）如图所示，在 v–t 图像中描点，在实验误差允许的范围内所描出的各点在同一条直线上，因此可得出结论：小车的速度随时间均匀变化，即小车做匀加速直线运动。由直线斜率求出其加速度 a = 1.94 m/s²（1.90 ~ 1.99 m/s²均可）。

 

5．（1）55 m/s；（2）276 m；（3）9.67 s

提示：（1）以竖直向下为正方向，则 a = 12 m/s²，根据 v² − v₀² = 2ah₂，运动员打开降落伞时的速度 v₀ = $\sqrt{v^2-2g{h}_2}$，代入数据得 v₀ = 55 m/s。

（2）运动员做自由落体运动下降的高度 h₁ = $\frac{v_0^2}{2g}$，代入数据得 h₁ = 151 m。所以离开飞机时距地面的高度 h = h₁ + h₂ = 151 m + 125 m = 276 m。

（3）运动员做自由落体运动的时间 t₁ = $\frac{v_0}{g}$，代入数据得 t₁ = 5.5 s。做匀减速运动的时间 t₂ = $\frac{v-v_0}{a}$，代入数据得 t₂ = 4.17 s。故运动员离开飞机后，到达地面所经历的时间 t = t₁ + t₂ = 5.5 s + 4.17 s = 9.67 s。

 

6．（1）因为物体做初速度为 0 的匀加速直线运动，设加速度为 a，在前 n 秒内的位移为x_n，由匀变速直线运动的位移公式，得 x_能 = $\frac{1}{2}$an²，所以 x₁∶x₂∶x₃∶… = 1∶4∶9∶…

（2）同理，前（n − 1）秒内的位移为 x_{n – 1} = $\frac{1}{2}$a(n – 1)²，故第 n 秒内的位移为 x_n = $\frac{1}{2}$an² − $\frac{1}{2}$a(n – 1)² = $\frac{a}{2}$(2n − 1)。则 x_Ⅰ∶x_Ⅱ∶x_Ⅲ∶… = 1∶3∶5∶…

（3）设物体在第 (n − 1) 个时间间隔内的初速度为 v₀，末速度为 v，则 v = v₀ + aT，s_{n −1} = v₀T + $\frac{1}{2}$aT²。同理可得 s_n = vT + $\frac{1}{2}$aT²。联立解得 s_n – s_{n – 1} = (v₀ + aT)T + $\frac{1}{2}$aT² – (v₀T + $\frac{1}{2}$aT²) = aT²。则 Δs = s₂ − s₁ = s₃ − s₂ = … = s_n − s_{n − 1} = aT²。

B 组

1．18 s 内的 v–t 图像如图所示。

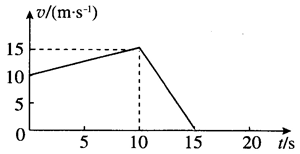
提示：汽车初速度 v₀ = 36 km/h = 10 m/s，以 0.5 m/s² 的加速度匀加速 10 s后，由 v = v₀ + at 得 v = 15 m/s，再以 3 m/s² 的加速度匀减速刹车，经 t₂ = $\frac{\mathrm{\Delta }v}{a}$ 停下，代入数据得 t₂ = 5 s，最后 3 s 汽车是静止的。

 

2．24 m/s

提示：汽车刹车前的速度为 v₀ = 108 km/h = 30 m/s。汽车在晴天行驶时，设刹车的加速度大小为 a₀，安全距离为 x₀，反应时间为 t₀，由匀变速直线运动的位移公式得x₀ = v₀t₀ + $\frac{v_0^2}{2a_0}$。汽车在雨天行驶时，设刹车的加速度大小为 a，安全行驶的最大速度为 v，由匀变速直线运动的位移公式得 x₀ = vt₀ + $\frac{v^2}{2a}$。又由 a = $\frac{3}{5}$a₀，联立解得以 a₀ = 5 m/s²，v = 24 m/s。

 

3．26 s；26 m/s；98 m

提示：x = 26 m，v_t = 12 m/s，a = 1 m/s²。设经过时间 t 汽车追上大客车，则由 $\frac{1}{2}$at² = v₁t + x，解得 t = 26 s。追上时，小汽车的速度 v₂ = at = 26 m/s。追上前，两车速度相等时，两车之间的距离 Δx 最大，此时 tʹ = $\frac{v_1}{a}$ = 12 s，则 Δx = x + v₁tʹ − $\frac{1}{2}$atʹ² = 98 m。

 

4．（1）0.2 m；（2）20 m/s；（3）20 m

提示：考虑到曝光时间极短，石子的平均速度近似等于瞬时速度；石子做自由落体运动，可以用自由落体的速度和位移关系式求解石子下落的高度。

（1）设在曝光时间 0.01 s 内，石子实际下落的距离为 l，由题意得 $\frac{4\mathrm{c}\mathrm{m}}{100\mathrm{c}\mathrm{m}}$ = $\frac{0.8\mathrm{c}\mathrm{m}}{l}$，解得 l = 20 cm = 0.2 m。

（2）石子在这 0.01 s 内的速度为 v = $\frac{l}{\mathrm{\Delta }t}$ = $\frac{0.2\mathrm{m}}{0.01\mathrm{s}}$ = 20 m/s。

（3）石子做自由落体运动，故 h = $\frac{v^2}{2g}$ = $\frac{{(20\mathrm{m}/\mathrm{s})}^2}{2\times 10\mathrm{m}/{\mathrm{s}}^2}$ = 20 m。

 

5．（1）t − $\sqrt{\frac{19}{20}}$t；（2）$\frac{t}{2}$；（3）$\frac{\sqrt{30}-5}{10}$

提示：子弹做匀减速运动穿过第 20 块木板后速度变为 0，运用逆向思维法，可以求出子弹做初速度为 0 的匀加速运动穿过 n 块木板所用的时间 t_n，设每块木板的厚度为 s，则有 ns = $\frac{1}{2}$at_n²，其中 1 ≤ n ≤ 20。因此当 n = 20 时，有 20s = $\frac{1}{2}$at²，所以有 $\frac{s}{a}$ = $\frac{t^2}{40}$。

（1）穿过第一块木板后 n = 19，有 19s = $\frac{1}{2}$at₁₉²。所以 t₁₉ = $\sqrt{2\times 19\times \frac{s}{a}}$ = $\sqrt{\frac{19}{20}}$t。因此，穿过第 1 块木板所用的时间为 t − $\sqrt{\frac{19}{20}}$t。

（2）穿过前 15 块木板，即 n = 5，有 5s = $\frac{1}{2}$at₅²。所以 t₅ = $\sqrt{2\times 5\times \frac{s}{a}}$  = $\frac{t}{2}$。

（3）穿过第 15 块木板前时 n = 5，有 6s = $\frac{1}{2}$at₆²。所以 t₆ = $\sqrt{2\times 6\times \frac{s}{a}}$ = $\sqrt{\frac{3}{10}}$t。

穿过第 15 块木板的时间 Δt = t₆ – t₅，解得 Δt = $\frac{\sqrt{30}-5}{10}$t。

 

6．（1）50 s；（2）22 s；27 s

提示：（1）v₁＝15 m/s、v₂＝5 m/s、x₀＝10 m、t₀＝20 s，a＝1 m/s²。走人工收费通道，汽车在减速、静止、加速三个阶段通过的位移 x₁＝$\frac{v_1^2}{2a}$×2，代入数据得 x₁ ＝ 225 m。所用时间 t₁ ＝$\frac{v_1}{a}$×2 ＋ t₀，代入数据得 t₁ ＝ 50 s。

（2）走 ETC 通道，汽车在减速、匀速、加速三个阶段通过的位移

x₂ ＝ $\frac{v_2^2-v_1^2}{-2a}$＋x₀＋$\frac{v_1^2-v_2^2}{2a}$，代入数据得 x₂ ＝ 210 m。

所用时间 t₂ ＝ $\frac{v_2-v_1}{-a}$＋$\frac{x_0}{v_2}$＋$\frac{v_1-v_2}{a}$，代入数据得 t₂ ＝ 22 s。

故节约时间 Δt ＝ t₁－（t₂＋$\frac{x_1-x_2}{v_1}$），代入数据得 Δt ＝ 27 s。