第五章 第五节 圆周运动的应用

 

 

 

 

 

 

 

 

 

 

 

 

 

图 5–43  转弯的火车

 

圆周运动的运动规律和物体做圆周运动的条件，在生活、生产和科学研究等方面有很广泛的应用。

我们知道，组成物质的分子总是在做永不停息的无规则运动。分子速率的测量对于分子热运动的研究具有重大意义。

1920 年，美国物理学家史特恩（O．Stern，1888－1968）提出了一种应用圆周运动规律测定气体分子速率的方法。史特恩实验装置如图 5–44 所示。A、B 为双层共轴圆筒形容器，内筒 A 半径为 r，外筒 B 半径为 R，内外筒可同时绕转轴 K 以同一角速度高速旋转；容器内部抽成高度真空，沿转轴 K 装有一根镀银的铂丝，铂丝通电加热使银蒸发成气体，一些银原子穿过筒 A 的狭缝 a 射出，最终落于筒 B 的内表面。由于银原子由内筒运动到外筒需要一定时间，若容器不动，这

 

些原子将到达外筒内壁上的 b 点；若容器以角速度 ω 旋转，这些原子将到达外筒内壁上的 bʹ 点。

设待测银原子的速率为 v，则原子由内筒运动到外筒所需时间为

\[\Delta t = \frac{{R - r}}{v}\]

而在此时间内，外筒上的 bʹ 点转过弧长为

\[\Delta s = R\theta = R\omega t\]

由上两式可得

\[v = \frac{{(R - r)R\omega }}{{\Delta s}}\]

实验中只需测得 R、r、ω、Δs，即可求得银原子的速率。

汽车、火车等在运动中经常会转弯（图 5–43），转弯时的运动可以看成局部的圆周运动，转弯必须有足够的向心力作用才能完成。

汽车在水平地面上转弯时，受重力、支持力和地面对车轮的静摩擦力，竖直方向的重力与支持力平衡，只有地面对车轮的静摩擦力提供汽车转弯所需的向心力。

如图 5–45 所示，火车轨道弯道处的外轨通常略高于内轨。当火车通过弯道时，车身会向弯道的圆心倾斜很小的角度 α，这时火车受到的支持力 F_N 与重力 G 的合力 F 沿水平方向，提供了火车转弯所需的向心力。

全自动洗衣机进入甩干程序后，在电动机的带动下，洗衣机的内筒会绕轴高速旋转。随着转速的增加，附着在衣物上的水需要的向心力越来越大，当衣物对水的附着力小于水

 

需要的向心力时，水就会离开衣物，从筒壁的小孔中飞出，一会儿衣物上的水就基本被甩掉了。

图 5–46 所示是做棉花糖的情景。砂糖颗粒在加热腔中熔化成糖液，当加热腔高速旋转时，由于缺少足够的向心力，糖液无法维持圆周运动，便从加热腔壁上的小孔飞出，遇冷凝结成固态的糖丝，聚成一团就成了棉花糖。

从上面的事例我们可以看到，做圆周运动的物体，如果受到的力不足以提供所需的向心力，物体就会远离圆心，这就是离心现象。

生活、生产中的离心现象有着广泛的应用，但有时也会造成危害，需要设法防范。

当汽车在道路上转弯时一定要减速慢行，尤其在雨雪天气、路面湿滑时，更要减速慢行，以防因摩擦力不足而发生离心现象——车辆发生侧滑，酿成车祸。

 

高速转动的砂轮、飞轮等，都不得超过额定的最大转速。如果转速过高，砂轮、飞轮内部的相互作用力不足以提供需要的向心力，砂轮、飞轮的某些组成部分会被高速甩出，这类离心现象可能酿成人身伤害等事故。

飞机由俯冲拉起或翻筋斗时，飞行员的血液由于离心运动会流向下肢，造成飞行员大脑缺血，感觉四肢沉重，这种现象叫做过荷。过荷太大时，飞行员会暂时失明，甚至晕厥。飞行员可以通过加强训练、增强体质来提高抗荷能力。图 5–47 所示就是飞行员进行提升抗荷能力训练的载人离心机。

图 5–47  载人离心机

 

问题与思考解读

1．参考解答：汽车通过弯道出口时的运动可近似看作局部的圆周运动，速度越大需要的向心力就越大，如果不减速，地面不能提供足够的向心力，容易发生汽车冲出弯道的事故。

命题意图：用圆周运动知识解释生活中的常见现象，巩固向心力的相关知识。

主要素养与水平：质疑创新（Ⅰ）；社会责任（Ⅱ）。

2．参考解答：

（1）舞蹈演员旋转时，裙摆因得不到足够的向心力而做远离圆心的运动，裙子张开。

（2）转动伞柄，伞面对水的附着力不足以提供水所需的向心力，水就被甩离伞面。

（3）车辆急转弯时，黄沙做圆周运动，如得不到足够向心力，黄沙就会被甩出。

命题意图：从实际情境中抽象物理模型，用物理语言解释生活中常见的现象，提升物理观念。

主要素养与水平：科学论证（Ⅱ）。

3．参考解答：汽车受到的重力和支持力平衡，静摩擦力提供向心力。由公式 F_f = m\(\frac{{{v^2}}}{r}\) 可得，最大安全速度 v = \(\sqrt {\frac{{{F_{f\max }}r}}{m}} \) =  \(\sqrt {\frac{{1.4 \times {{10}^4} \times 50}}{{2.0 \times {{10}^3}}}} \) m/s ≈ 18.71 m/s。

命题意图：用向心力公式计算车辆转弯的最大安全速度，熟悉向心力公式，提升安全意识。

主要素养与水平：科学推理（Ⅱ）；社会责任（Ⅱ）。

4．参考解答：高速转弯时赛车冲出赛道；长发女孩快速旋转时，头发会“飘”起来……

命题意图：引导学生关注生活，理解离心现象。

主要素养与水平：运动与相互作用（Ⅱ）。

5．参考解答：子弹的运动可看作匀速直线运动，纸筒匀速转动，子弹运动距离 l 的时间与纸筒转过 2πn + θ（n = 0，1，2，…）的时间相等，即 \(\frac{l}{v}\) = \(\frac{{2\pi n + \theta }}{\omega }\) ，解得 v =  \(\frac{{l\omega }}{{2\pi n + \theta }}\)（式中 n 为正整数）

命题意图：思考圆周运动的周期性问题，结合直线运动、圆周运动的规律解决比较复杂的问题，提升分析问题、解决问题的综合能力。

主要素养与水平：运动与相互作用（Ⅲ）；科学推理（Ⅲ）。

参考资料

铁轨引导的转弯

与汽车不同，火车没有方向盘，行驶在铁轨上的火车，行驶方向完全由铁轨引导。如图 9 所示，在火车车轮内侧有一圈比轮子稍大一点的圆盘，叫做轮缘，遇到弯道或岔道时，轮缘起到导车转弯或换道。

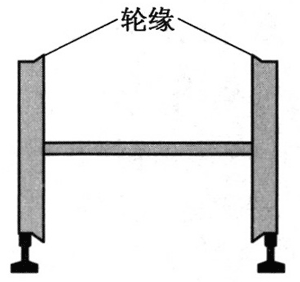
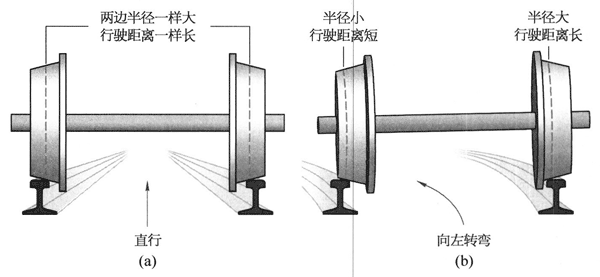
火车的车轮并不是平整的圆柱体，而是圆台。这一设计可以帮助火车顺利通过弯道。火车在直道上行驶时，两侧的车轮以等大的轮半径分别在两边的轨道上滚动，如图 10（a）所示；若列车向左转弯，由于惯性，车体会偏向右侧，导致右侧车轮与轨道接触点处的车轮半径较大，左侧半径较小，如图 10（b）所示（从车尾看）。这样，由于存在半径差，右轮在右侧弯轨上行驶的路程大于左轮行驶的路程，就可以使车轮完成转向了。

设计高速铁路时，为满足列车高速运行的需要，转弯半径就应当加大。一般情况下，不同设计时速的高速铁路对应的最小转弯半径如下表所示。

 

设计时速（km/h）	250	300	350
最小转弯半径（m）	4 000	4 500	7 000

 

我国新建高速铁路一般逢山开隧、遇水架桥，线路较为平直，大多数路段为直线或大半径曲线，为高速铁路时速的提升做好了充分的准备。

菲索齿轮法测光速

人们现在都知道，真空中光速为 3×10⁸ m/s，这么大的光速是怎么测出来的呢？意大利物理学家伽利略在 1607 年进行了世界上第一次测量光速的尝试。他让两个人分别站在相距数千米的两座山上，每人拿一盏灯，第一个人先亮灯，当第二个人看到第一个人的灯亮时立即亮起自己的灯，根据第一个人亮灯到他看到第二个人亮灯的时间间隔来计算光速。因为光的传播速度太大，加之观察者还要有一定的反应时间，实验方法过于粗糙，实验没有成功。

1849 年，法国物理学家菲索采用旋转齿轮法测量光速。此法原则上与伽利略提出的方法相似，不过用反射镜代替了第二个观察者，用旋转的齿轮代替了手动亮灯的开关。

齿轮法的装置如图 11 所示。光源 S 发出的光照射到半透明的玻璃片 M₁ 上，一部分光被 M₁ 反射。在光的传播路径上，有一个转速可调的齿轮 W，它的齿隙不遮光，而它的齿却能遮住来自 M₁ 的光。通过齿隙的光经过相当长的距离 L 到达平面镜 M₂ 后再次被反射并沿原路返回。如果齿轮不动，返回的光会穿过同一齿隙，被位于半透明玻璃片 M₁ 后的观察者看到。

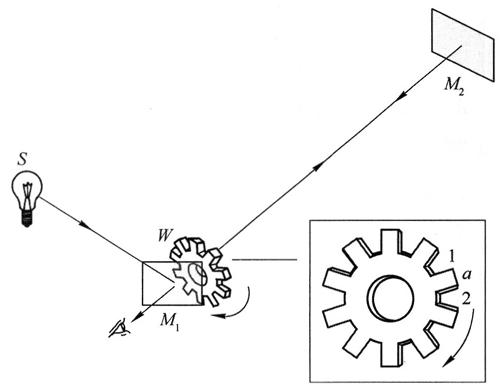
转动齿轮，齿轮速度较小时，穿过齿隙 1 的光被 M₂ 反射后仍穿过齿隙 1 进入观察者的眼睛。当齿转到光的传播路线上时，光将被遮住，观察者看不到光。因此，来自 M₁ 的光交替照射到齿隙和齿，观察者将看到闪光。

随着齿轮转速的增大，观察者每次看到亮光的时间越来越短。齿轮转速增大到某一数值时，穿过齿隙 1 的光被 M₂ 反射后再返回到齿轮时，恰被紧邻的齿 a 挡住，观察者看不到亮光；转速继续增大，当由 M₂ 返回的光恰好穿过齿隙 2 时，观察者再次看到亮光。

设齿轮的转速为 n，齿轮的齿数为 N，则观察者第一次看不到亮光时，齿 a 转到齿隙 1 的位置所需的时间为

\[\Delta t = \frac{1}{{2Nn}}\]

在这段时间内，光由齿轮传播到 M₂，又由 M₂ 返回到齿轮，走的路程为 2L，所以光速 c 为

\[c = \frac{{2L}}{{\Delta t}} = 4LnN\]

菲索用的齿轮齿数为 N = 720，在巴黎市郊柏距约 8 km 的两地之间进行测量，2L = 1.726 6×10⁴ m，发现第一次看不见光时，齿轮的旋转速度为 12.6 r/s，由此测得 c = 3.13×10⁸ m/s。这个实验中，主要的误差是很难精确地定出看不见光的条件，但菲索的结果已经很接近实际的光速。菲索之后，又有许多人先后改进了这个实验，所得结果均在 2.99×10⁸ m/s 和3.01×10⁸ m/s 之间。

惯性离心力

如图 12 所示，水平圆盘上有一径向直槽，槽内弹簧一端固定于圆心 O，另一端系一小球。当圆盘以均匀角速度旋转时，弹簧伸长，小球相对圆盘静止。在位于地面的观察者甲看来，小球受到弹簧的拉力，使之产生向心加速度做圆周运动。如有另一观察者乙位于圆盘上，则在他看来，此时小球静止必受平衡力作用，除受到弹簧伸长导致的回复力以外，同时还受到一个与回复力大小相等、方向相反的惯性力，否则小球不会静止。这个沿径向向外的力叫做惯性离心力，也就是平常所说的“离心力”。

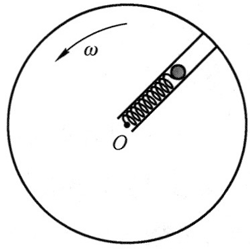
两位观察者的看法不同，是因为他们所处的参考系不同。甲处于相对地面静止的参考系（可看作是惯性系），乙处于转动参考系（即非惯性系）。对甲来说，是不存在“离心力”的，也就是说，在惯性系中是没有“离心力”的，惯性离心力是存在于转动参照系中的。在转动参考系中引入惯性离心力，可使牛顿运动定律继续成立。