第五章 第一节 曲线运动

图示为游乐场内过山车的照片。过山车是一种颇受人们欢迎的游乐项目,过山车上的游客随过山车沿轨道做曲线运动。曲线运动与之前学过的直线运动有不同的特点,具有更复杂的规律。过山车上的游客在运动过程中的速度、加速度是如何变化的?受力情况又是怎样的?
过山车是一种常见的游乐设施,很多学生都体验过这个项目,能回味在随过山车一起做曲线运动时惊险和异样的感受。用此图作为本章的情境引入可以使学生产生共鸣,激发学习曲线运动的兴趣。
同时,在学习圆周运动的应用时,可以运用此运动模型进一步讨论在竖直平面内圆周运动轨道的最高点与最低点的动力学规律。
第五章
- 在本章中我们将:
1.了解物体的曲线运动及其条件,认识平抛运动规律,用线速度、角速度和周期等概
念描述匀速圆周运动。
2.通过实验探究平抛运动和匀速圆周运动的规律。
3.运用运动合成与分解的方法分析生活中的抛体运动,运用牛顿第二定律分析匀速圆
周运动,了解离心现象及其成因。
- 本章的学习将用到机械运动的概念和匀速直线运动的规律。
- 本章的学习有助于运动观念的形成,并为研究变速直线运动的规律奠定基础。
学习目标
1.初步形成曲线运动的概念,能用平抛运动、匀速圆周运动的规律解释或解决生活中的简单问题。
2.通过观察和实验了解曲线运动,知道物体做曲线运动的条件,认识平抛运动、匀速圆周运动的规律,体验将复杂运动分解为简单运动的物理思想,体会物理学中实验过程和理论推导的方法,以及化繁为简的研究方法。
3.通过探究平抛运动特点的实验和探究向心力大小与半径、角速度、质量关系的实验,学会设计实验方案,进行实验并获得数据、分析数据,进而归纳出实验结论、作出解释。能撰写简单的实验报告。
4.结合车辆转弯、离心现象和分子速率测定等与生活实际及科技研究相关的事例分析,知道科学、技术、社会之间存在密切的关系。
编写意图
课程标准中对本章内容的要求为:
2.2.1 通过实验,了解曲线运动,知道物体做曲线运动的条件。
2.2.2 通过实验,探究并认识平抛运动的规律。会用运动合成与分解的方法分析平抛运动。体会将复杂运动分解为简单运动的物理思想。能分析生产生活中的抛体运动。
2.2.3 会用线速度、角速度、周期描述匀速圆周运动。知道匀速圆周运动向心加速度的大小和方向。通过实验,探究并了解匀速圆周运动问心力大小与半径、角速度、质量的关系。能用牛顿第二定律分析匀速圆周运动的向心力。了解生产生活中的离心现象及其产生的原因。
本章内容是在直线运动规律的知识基础上进行曲线运动的学习,在拓展对运动多样性的认识和分析过程中,深化对位移、速度、加速度等重要概念的理解,进一步提升关于力与运动关系的认识。
本章从生活中的曲线运动如投出篮球的运动等事例开始,引导学生了解曲线运动的特点。通过“自主活动”“大家谈”等栏目,经历将具体运动抽象的过程,认识曲线运动的速度方向、受力情况等规律,认识描述匀速圆周运动的线速度、角速度等物理量;通过研究平抛运动、匀速圆周运动等运动形式,体会物理学中实验和理论推导的方法,以及化繁为简的研究方法;结合车辆转弯、离心现象和分子速率测定等事例的分析,体会曲线运动规律与实际问题的联系。本章重点关注从现象归纳规律、运用规律解释现象的认知过程。
本章内容的学习要注重对运动观念的进一步提升,还应注重创设运用物理规律解释或解决实际问题的情境,为分析实际生活中的复杂运动奠定基础。
完成本章内容的学习,共需要 9 课时。其中,第一节 1 课时,第二节 2 课时,第三节 2 课时,第四节 2 课时,第五节 2 课时。

图 5–1 滑雪
滑雪运动是学生熟知的曲线运动。本节利用滑雪运动图片引出曲线运动的情境,使学生感知曲线运动的速度方向是变化的,这正是本节要讨论的重点。
本节编写思路
本节通过滑雪、投出的篮球及行驶的自行车等图片,用生活中常见事例为引导,引出本节讨论的主题,建立曲线运动的概念。
通过演示实验、“自主活动”等环节,让学生了解做曲线运动物体的速度方向的规律及物体做曲线运动的条件,进而思考曲线运动有何规律等问题。
通过介绍伽利略对曲线运动的研究方法,引出运动合成与运动分解的研究思路,让学生体会将复杂运动分解为简单运动的物理思想。
在学习过程中所经历的观察、实验、思辨等过程,有助于学生掌握研究方法、理解运动规律,并解释和描述常见的曲线运动,以及探讨生产生活中的复杂运动等。
在日常生活中,物体的运动轨迹一般是比较复杂的曲线。物体沿曲线所做的运动叫曲线运动(curvilinear motion)。图 5–1 中的滑雪运动员、图 5–2(a)中投出的篮球和图 5–2(b)中行驶的自行车所做的运动都是曲线运动。
做曲线运动的物体,在不同时刻、不同位置的运动方向一般都是不同的。

(a)

(b)
图 5–2 常见的曲线运动

图 5–3 纸板陀螺
如图 5–3 所示,用牙签和圆形硬纸板制作一个纸板陀螺,在纸板边缘滴上墨水,将陀螺放在白纸上,旋转陀螺使墨水飞出,观察墨水在白纸上留下的径迹。
此处设置“自主活动”是为了使学生能直观地观察到,做曲线运动的物体在某点的瞬时速度方向沿曲线在该点的切线方向,同时可以观察到各点的速度方向是不同的。这种现象意味着陀螺边缘任意一点在运动过程中的速度是变化的,说明做曲线运动的物体具有加速度。
在纸板陀螺的实验中,可以先使纸板陀螺在水平放置的白纸上旋转,待其旋转稳定后再用滴管将墨水滴到陀螺边缘,就可观察到墨水飞出,并在白纸上留下径迹。
可以观察到,墨水沿圆纸板的切线方向飞出。
图 5–4 曲线运动速度的方向
大量事实表明,做曲线运动物体速度的方向是时刻改变的,物体在某一点的瞬时速度方向沿曲线在该点的切线方向,如图 5–4 所示。
速度是矢量,不论速度的大小是否改变,只要速度的方向改变,就表示速度发生了变化,所以曲线运动是变速运动,做曲线运动的物体具有加速度。
图 5–5 重力使投出的篮球做
曲线运动
对投出的篮球进行分析,可以发现篮球受到的重力与速度方向是不同的,如图 5–5 所示。
通过分析做曲线运动的篮球的受力情况,得出其所受合力方向与运动方向不同,根据牛顿第二定律,得出其加速度方向与速度方向不同,从而得出物体做曲线运动的条件。
通过分析和演绎得出重要结论的方法,将有助于提高学生运用已有物理原理进行模型建构、科学推理等方面的能力。
根据牛顿第二定律,物体的加速度方向与物体受到的合力方向一致。当合力的方向与速度方向不同时,加速度方向也就与速度方向不同,物体运动的速度方向就会发生改变而做曲线运动。
可见,物体做曲线运动的条件是:物体所受合力的方向与其速度方向不在同一直线上。

图 5–6 吹乒乓球
在水平桌面上,一个乒乓球沿斜面滚下后做直线运动。如图 5–6 所示,从侧面用力吹乒乓球,使乒乓球运动经过指定位置,应该如何吹才能完成任务?
此处设置“自主活动”是为了让学生进一步体验物体是如何做曲线运动的,深刻体验物体做曲线运动的条件,同时培养学生的实验探究能力和发散思维能力。
活动可按以下步骤进行:① 让乒乓球沿斜面滚下做直线运动;② 在垂直于其运动轨迹的方向吹乒乓球,观察它的运动轨迹;③ 试着在不同位置吹,直到乒乓球经过指定位置;④ 总结吹乒乓球成功入位的经验。通过此活动的探究过程,可启发学生如何把物体沿某一曲线的运动与其沿两个不同方向上的分运动联系起来,为形成运动合成相关概念做铺垫。
图 5–7 行驶的帆船
运动的叠加原理 · 一个运动可以看成两个或几个运动的合成或叠加,这两个或几个运动是同时进行的且互不干扰。
早在 17 世纪,伽利略就已经提出了研究曲线运动的方法,他认为可以把曲线运动分解为两个相互垂直方向的运动。设想石块从一艘匀速行驶的帆船桅杆顶部下落;并假定当船停着不动时,石块从桅杆顶部落到甲板需要的时间相当于脉搏跳动 2 次的时间。当船向前匀速航行时,使石块从桅杆顶部同一位置落下,石块落到甲板上时间不变,石块的运动轨迹就是一条曲线,如图 5–7 所示。
教材图 5–7 中“行驶的帆船”的问题早在17世纪前就有不少学者做了思考和解释,伽利略利用他的惯性原理想通了这个问题。对于站在岸上的观察者来说,在帆船停靠在岸边和匀速行驶的两种情况下,石块的运动是不同的。当帆船停靠在岸边时,站在岸上的观察者看到石块做自由落体运动;当帆船匀速行驶时,石块不仅在竖直方向做自由落体运动,而且由于惯性,它同时还要沿水平方向做匀速直线运动,因此它的运动路径是图中虚线所示,是这两个运动的合成。
利用伽利略的思路,可引出研究曲线运动的方法,即可把它看成两个简单直线运动的组合的科学方法。
此处设置“助一臂”是为了说明运动合成与分解的基本原理,包括如下运动的特性:
(1)运动独立性:各分运动之间是互不相干的,即各个分运动均按各自规律运动,彼此互不影响。因此在研究某个分运动时,不需要考虑其他分运动。
(2)运动等时性:各个分运动与合运动总是同时发生,同时结束,经历相等的时间。因此,若已知某一分运动的时间,也就知道了其他分运动经历的时间;反之亦然。
(3)运动等效性:各个分运动叠加起来的效果就是合运动,描述运动的物理量如位移、速度、加速度等,均为各分运动物理量的矢量和,这就是运动的叠加原理。
石块所做的曲线运动可看成是由竖直方向的自由落体运动和水平方向的匀速直线运动组合而成的。这两个运动称为石块的分运动,而它们的合运动就是石块所做的曲线运动。
在研究曲线运动时,通常把它看成两个简单直线运动的组合,从而使问题变得容易研究。
既然一个运动可以看成两个分运动的组合,那么只要知道每个分运动的规律,就可以得到合运动的规律。由于描述物体运动的位移、速度和加速度等物理量都是矢量,那么,两个分运动在一段时间内的位移、速度和加速度等物理量的矢量和就是该段时间内物体合运动的位移、速度和加速度。这种已知分运动求合运动的方法,称为运动的合成。
反之,由已知的合运动求分运动的方法,称为运动的分解。
把石块开始下落的点设为坐标原点 O,以水平向右和竖直向下分别为 x 轴和 y 轴的正方向建立平面直角坐标系,如图 5–8 所示。然后,分别研究 x 轴、y 轴这两个方向的分运动——直线运动的规律,得出两个分运动的位移、速度和加速度。最后根据矢量合成的平行四边形定则,得到石块合运动的位移、速度和加速度。
图 5–8 运动的分解与合成
设江水的流速为 6 km/h,轮船在静水中行驶的速度为 12 km/h。当驾驶员驾驶轮船垂直向对岸方向航行时,轮船实际行驶的方向如何?速度大小为多少?如果江面宽 200 m,轮船将行驶到对岸何处?
此处设置“自主活动”是对前面学习的运动合成与分解方法的应用。通过对“渡江问题”的分析和讨论,感受运用运动合成与分解的方法对研究比较复杂的运动的重要性,为后续研究平抛运动打下基础。
参考答案:轮船实际航向为偏向江水流动方向,与江岸夹角约 63.4°;轮船相对于岸的速度大小约为 13.4 km/h;轮船将行驶到对岸沿江水流动方向下游 100 m 处。
可见,在研究比较复杂的运动问题时,运用运动合成与分解的方法往往是十分有效的。同时,这一方法的运用要注意合运动与分运动之间、各分运动之间都具有等时性的特点。

图 5–9
图 5–10
- 如图 5–9 所示,图中的虚线为某同学投出篮球的运动轨迹。请标出篮球在图示位置所受的力和速度矢量。
- 运动员以 10 m/s 的速度沿与水平面夹角为 30° 的方向斜向上推出一铅球,这个速度在水平方向和竖直方向的分速度分别是多大?画出速度分解的图示。
- 如图 5–10 所示,一质点沿 AB 方向做匀速直线运动,当质点运动到 B 点时加上一个力 F。此后该质点的运动轨迹最接近中哪条虚线,简述理由。
- 一艘渡船在宽为 d 的河中航行。现从码头出发,船头垂直于河岸,以速度 v 匀速向对岸行驶。问:
(1)若河水流速处处为 u,渡船将停靠在对岸哪个位置?
(2)若越靠近河中央水的流速越大,试定性画出该船行驶的轨迹示意图。
- 某飞机以 30° 仰角起飞,起飞时初速度大小为 100 m/s。假设其做加速度大小为 1 m/s2 的匀加速直线运动。则:
(1)起飞后 10 s 末飞机离地面多高?
(2)此时刻飞机距起飞点的水平距离为多少?
- 在学校趣味运动会“运动击杆”的比赛中,要求运动员坐在一辆由西向东运动的小车上抛出一小球,击中位于小车左侧(北边)路边的一根旗杆,运动员应如何抛出小球才能击中目标?请画出示意图并说明理由。
问题与思考解读
1.参考解答:见图 1(受到重力 G 竖直向下;速度 v 沿篮球运动轨迹的切线方向向前)。
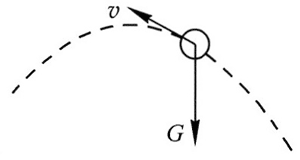
命题意图:通过实例分析与作图,体会物体做曲线运动时受到偏离运动方向的力的作用,其速度方向必将改变。
主要素养与水平:运动与相互作用(Ⅰ);模型建构(Ⅰ)。
2.参考解答:铅球水平方向的分速度为 vx = vcos30° ≈ 8.66 m/s,竖直方向的分速度为 vy = vsin30° = 5 m/s。见图 2。
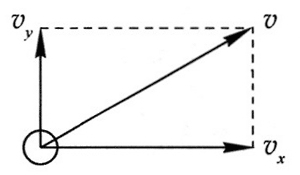
命题意图:通过对速度分解的计算与作图,体会用运动分解法研究实际运动的方法。
主要素养与水平:运动与相互作用(Ⅰ);模型建构(Ⅰ)。
3.参考解答:对质点施加力 F 后,质点受到的合力就为 F,它与质点原运动方向不在一条直线上。由 F 的方向推断,此后该质点的运动轨迹最接近图中的 BQ 虚线。
命题意图:体验运用曲线运动产生的条件分析与判断质点的运动轨迹。
主要素养与水平:运动与相互作用(Ⅰ);科学推理(Ⅰ)。
4.参考解答:(1)渡船将停靠在对岸沿河水流动方向下游距码头正对岸 s = \(\frac{{ud}}{v}\) 处。
(2)见图 3。
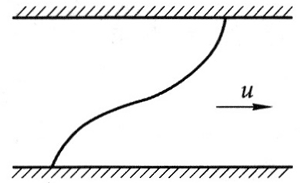
命题意图:体验运用运动合成与分解的方法研究问题,运用各分运动具有等时性的特点研究较复杂的运动,为后续学习平抛运动的轨迹做准备。
主要素养与水平:运动与相互作用(Ⅱ);科学推理(Ⅱ)。
5.参考解答:(1)根据匀加速直线运动规律,s = v0t + \(\frac{1}{2}\)at2 = 1 050 m,所以飞机离地面高度为 h = ssin30° = 525 m。
(2)距起飞点的水平距离为 x = scos30° ≈ 909.33 m。
命题意图:运用运动合成与分解的思路和方法解决物体做匀变速运动时的实际问题。
主要素养与水平:运动与相互作用(Ⅱ);模型建构(Ⅱ);科学推理(Ⅱ)。
6.参考解答:应在小车尚未到达旗杆正前方之前抛出小球;且需控制好抛出的速度大小,使小球的水平(合)运动恰好对着旗杆。见图 4。
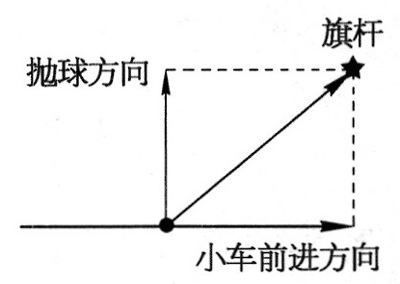
命题意图:在实际的运动情境中,运用运动合成与分解的方法进行模型建构、问题分析及实践探究。
主要素养与水平:模型建构(Ⅲ);科学推理(Ⅱ);科学论证(Ⅱ)。
发布时间:2022/1/30 下午9:47:40 阅读次数:10323
