第 4 章 万有引力定律及航天 第 2 节 万有引力定律的应用

万有引力定律的发现，不仅解决了行星的运行问题，也为人们开启了“飞天”的理论之路。那么，人造卫星要以多大的速度环绕地球运动才能不落回地面？“嫦娥四号”探测器又是怎样飞向神秘的月球的？本节我们将运用万有引力定律来研究天体的运动，探讨人造卫星的发射原理，认识科学定律对人类探索未知世界的作用。

1．天体质量的计算

如何运用引力常量计算出地球的质量？重力的存在主要是因为地球对物体有引力作用，如果不考虑地球的自转，可以认为在地面附近重力等于万有引力，即

mg = G \(\frac{{mM}}{{{R^2}}}\)

式中，R 为地球的半径， m 为物体的质量，M 为地球的质量。由此可以估算出地球的质量。

拓展一步

重力与万有引力的关系

如果考虑地球的自转，物体的重力与万有引力并不相等。如图 4-12 所示，若将地球看成质量分布均匀的球体，地球对物体的万有引力 F 的方向指向地心 O；物体的重力 mg 只是万有引力的一个分力，方向竖直向下；万有引力的另一个分力 F′ 提供物体随地球自转所需要的向心力。进一步计算表明，物体受到的重力与万有引力相差不大，因此，在粗略计算中可认为重力近似等于万有引力。

图 4-12 重力与万有引力分析示意图

还有另一种方法可计算天体的质量。假设质量为 m 的天体 A，围绕质量为 M 的天体 B 近似做匀速圆周运动（图 4-13），天体 A 所需要的向心力

F = mω²r = m（\(\frac{{2\pi }}{T}\)）²r

图 4-13 天体 A 绕天体 B 做匀速圆周运动的示意图

此向心力由天体 B 对天体 A 的万有引力提供，即

G \(\frac{{mM}}{{{r^2}}}\) = m（\(\frac{{2\pi }}{T}\)）²r

由此可解得天体 B 的质量

M = \(\frac{{4{\pi ^2}{r^3}}}{{G{T^2}}}\)

由上式可知，只要知道某小天体围绕某中心大天体做圆周运动的周期和两天体之间的距离，就可求出中心大天体的质量。

已知月球绕地球运行的周期 T = 27.3 天，月球与地球的平均距离 r = 3.84×10⁸ m，由此可估算出地球的质量

M = \(\frac{{4 \times {{3.14}^2} \times {{(3.84 \times {{10}^8})}^3}}}{{6.67 \times {{10}^{ - 11}} \times {{(24 \times 3600 \times 27.3)}^2}}}\) = 6.02×10²⁴ kg

请查阅资料，算一算太阳的质量。

2．人造卫星上天

为什么宇宙飞船能像月球那样围绕地球旋转？宇宙飞船在什么条件下能挣脱地球的束缚？

在《自然哲学的数学原理》一书中，牛顿用一幅图解释了行星能保持在某轨道运行的原因（图 4-14）。从抛体运动的角度考虑，如投掷一块石头，该石头本应做直线运动，但因其自身重力，石头做曲线运动，最终落到地面；投掷速度越大，落地点距投掷点就越远。只要抛出的速度足够大，被抛出的物体就不再掉下来。这实际上就是人造地球卫星或宇宙飞船上天的原理。

图 4-14 牛顿的抛体运示意图

如何使人造卫星和宇宙飞船获得足够大的初始速度？1903 年，动俄国科学家齐奥尔科夫斯基（K.Tsiolkovski，1857—1935）提出了液体火箭发动机的构想，首次阐述了如何利用多级火箭克服地球引力实现宇宙航行。正是基于这种构想，人类在 1957 年成功发射了第一颗人造地球卫星。图 4-15 展示了用多级火箭发射卫星，使卫星进入轨道的大致过程。

图 4-15 火箭推动卫星进入轨道的示意图

如果卫星绕地球运行的轨道可视为圆形，并且卫星距地面的高度远小于地球半径，则卫星轨道半径可近似视为地球半径 R = 6.4×10⁶ m，这时卫星所受地球的引力与卫星做圆周运动所需的向心力相等。假设卫星质量为 m，地球质量为 M，根据向心力公式有

G \(\frac{{Mm}}{{{R^2}}}\) = m \(\frac{{{v^2}}}{R}\)

由此可得，卫星在地面附近轨道绕地球做匀速圆周运动所必需的运行速度

v = \(\sqrt {\frac{{GM}}{R}} \) = \(\sqrt {\frac{{6.67 \times {{10}^{ - 11}} \times 5.98 \times {{10}^{24}}}}{{6.4 \times {{10}^6}}}} \) m/s = 7.9 km/s

人们称 7.9 km/s 为第一宇宙速度（first cosmic velocity），也称环绕速度。

如果人造地球卫星发射的速度大于 7.9 km/s，它将沿椭圆轨道围绕地球运行，甚至会摆脱地球引力，远离地球而去。通过计算可知，人造卫星脱离地球引力所需的速度为 11.2 km/s，人们称之为第二宇宙速度（second cosmic velocity），也称脱离速度（图 4-16）。

图 4-16 不同宇宙速度对应不同轨道的示意图

脱离地球引力的人造卫星还受到太阳引力的作用，相当于“人造行星”。当其发射速度达到 16.7 km/s 时，就会挣脱太阳引力的束缚，飞出太阳系。人们称 16.7 km/s 为第三宇宙速度（third cosmic velocity），也称逃逸速度。

物理聊吧

图 4-17 是“阿波罗十一号”宇宙飞船的登月往返航线示意图。

（a）从地球飞往月球

（b）从月球飞往地球

图 4-17 “阿波罗十一号”登月往返航线示意图

经火箭发射，“阿波罗十一号”宇宙飞船首先进入环绕地球的轨道，然后加速，脱离环绕地球轨道后，惯性飞行，进入环绕月球的轨道，最后登月舱降落在月球（红色轨迹）。

当宇航员在月球上完成工作后，再发动引擎进入环绕月球的轨道，然后加速，脱离环绕月球轨道，进入环绕地球轨道，最后降落于地球（绿色轨迹）。

结合登月往返航线讨论：为什么飞船能围绕地球旋转？飞船在什么条件下能挣脱地球的束缚？为什么飞船能围绕月球旋转？飞船在什么条件下能挣脱月球的束缚？

例题

我国的量子科学实验卫星“墨子号”于 2016 年 8 月 16 日在酒泉成功发射，其升空后围绕地球的运动可视为匀速圆周运动，离地面的高度为 500 km（图 4-18）。已知地球的质量约为 6.0×10²⁴ kg，地球的半径约为 6.4 × 10³ km，求“墨子号”运动的线速度大小和周期。

分析

卫星绕地球做匀速圆周运动，地球对卫星的万有引力提供向心力。可由向心力公式求解。

解

由题意可知，“墨子号”距地面高度 h = 5.0 × 10⁵ m，地球半径 R = 6.4 × 10⁶ m，地球质量 M = 6.0 × 10²⁴ kg。设 m 为“墨子号”的质量，r 为地球球心到“墨子号”的距离。

由           \(G\frac{{Mm}}{{{r^2}}} = m\frac{{{v^2}}}{r}\)

其中       r = R + h

可得

\(\begin{array}{l}v = \sqrt {\frac{{GM}}{r}} \\ = \sqrt {\frac{{6.67 \times {{10}^{ - 11}} \times 6.0 \times {{10}^{24}}}}{{6.4 \times {{10}^6} + 5.0 \times {{10}^5}}}} {\rm{m/s}}\\ = 7.6 \times {10^3}{\rm{m/s}}\end{array}\)

周期

\(\begin{array}{l}T = \frac{{2\pi (R + h)}}{v}\\ = \frac{{2 \times 3.14 \times (6.4 \times {{10}^6} + 5.0 \times {{10}^5})}}{{7.6 \times {{10}^3}}}{\rm{s}}\\ = 5.7 \times {10^3}{\rm{s}}\end{array}\)

讨论

人造地球卫星绕地球做圆周运动的线速度、角速度、周期和向心加速度与哪些因素有关？

策略提炼

当中心天体质量很大，卫星绕中心天体做匀速圆周运动时，可认为中心天体不动，卫星所需要的向心力由中心天体对它的万有引力提供。由向心力公式建立关系式 G\(\frac{{Mm}}{{{r^2}}}\) = ma，是解决天体运动问题的基本思路和方法之一。

迁移

地球同步卫星是相对地面静止的卫星，卫星的运行方向与地球自转方向相同，运行轨道为位于地球赤道平面上的圆形轨道，运行周期与地球自转周期相等。请定性比较地球同步卫星与“墨子号”二者的轨道半径、线速度及向心加速度的大小。

科学书屋

人造卫星——人类的“千里眼”“顺风耳”

人造卫星是人类的“千里眼”和“顺风耳”。人造卫星种类很多、用途各异，有科学卫星、气象卫星（图 4-19）、地球资源卫星、环境检测卫星和照相侦察卫星等，卫星上的照相机和雷达等设备可以帮助人们看得更远、更深入。

卫星上的接收器和转发器可以帮助人们接收和转发信息。例如，通信卫星可以把相距遥远的两地连接起来，即使是边远地区也可以进入通信网络。尤其是静止通信卫星（也叫地球同步卫星），为人类通信带来了极大方便。静止通信卫星绕地球运行一周的时间和地球自转一周的时间相同，在地球上观察，赤道上方与地球同步运行的通信卫星总是静止不动的。从理论上来说，发射三颗等距分布在地球同步轨道上的静止通信卫星就几乎可以实现全球通信了。

3．预测未知天体

目前科学家已确认太阳系有八大行星，按距太阳由近及远的顺序依次为水星、金星、地球、火星、木星、土星、天王星和海王星。它们在各自的椭圆轨道上绕太阳运转，如图 4-20 所示。

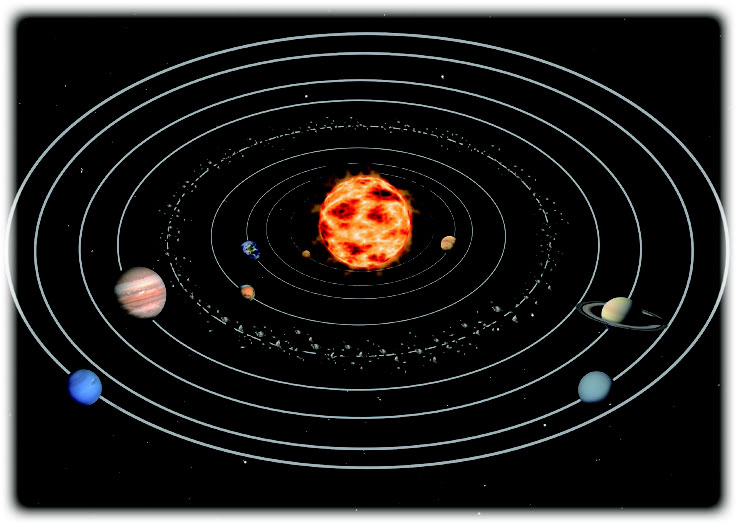
水星、金星、火星、木星及土星都是人们用肉眼直接观察到的。1781 年，人们第一次通过天文望远镜发现了新的大行星——天王星。天文学家在观察天王星时，发现它绕太阳的运行轨道与由万有引力定律计算出来的轨道不吻合。于是，有些人开始怀疑万有引力定律的正确性；也有人运用万有引力定律预测，可能在天王星外还有一颗未知的大行星。

1845 年，英国大学生亚当斯计算出了这颗未知行星的轨道和质量，但未引起重视。几乎同时，法国天文爱好者勒维耶也独立计算出了这颗未知行星的位置。1846 年 9 月 23 日，德国天文学家伽勒在勒维耶预测的区域发现了这颗神秘的行星——海王星。

海王星的发现是科学史上的奇迹，因为它是人们通过计算发现的。通过万有引力定律成功地预测未知的星体，不仅巩固了万有引力定律的地位，也充分展示了科学理论的预见性。

素养提升

能了解万有引力定律的内涵，会计算人造卫星的环绕速度，知道第二宇宙速度和第三宇宙速度；能用万有引力定律解释一些天体运动问题。具有与万有引力定律相关的运动与相互作用的观念。

——物理观念

方法点拨

利用科学理论不仅能解释已知的现象，还能预言一些未知的事物和现象。例如，科学家运用万有引力定律成功预测了海王星的存在。后来在天文学领域，基于相对论，爱因斯坦又预言了一系列重要事件和现象。

科学书屋

哈雷彗星

英国物理学家哈雷（E．Halley，1656—1742）通过观察、计算分析等，认为1531 年、1607 年和 1682 年出现的彗星，实际上是同一颗彗星的三次回归，并预言这颗彗星将于 1759 年再次出现。果然，这颗美丽的彗星在哈雷预计的时间段拖着长长的尾巴，又一次出现在星空中。为了纪念哈雷，大家将这颗彗星命名为哈雷彗星。后来，人们预测这颗彗星将分别于 1835 年、1910 年和 1986 年回归地球，结果它都如期而至（图 4-21）。

人们预测它在 2061 年还将回归地球。让我们共同等待它的出现吧！

节练习

1．同步卫星是与地球自转同步的卫星。请问，能否将同步卫星定点在北京上空？请说明理由。

【答案】不能。地球同步卫星若不在赤道所在平面上，假设实现了“同步”，那它受到地球的万有引力就不指向做圆周运动所在圆的圆心，不可能做稳定的圆周运动。因此，地球同步卫星必须定点在赤道的正上方。

2．为满足不同领域的需要，我国有许多不同轨道高度的人造卫星。如图所示，在某一轨道平面上有人造卫星 A、B 都绕地球做圆周运动，两颗人造卫星的质量之比为 1∶2，到地球球心的距离之比为 2∶3，则它们的

A．周期之比为 3∶2                        B．线速度大小之比为 \(\sqrt 3 \)∶\(\sqrt 2 \)

C．向心加速度大小之比为 4∶9      D．向心力大小之比为 1∶18

【答案】B

3．某卫星在距离地心 4R （R 是地球的半径）处，由于地球对它的引力作用而产生的加速度是地球表面重力加速度的多少倍？

【答案】\(\frac{1}{{16}}\)

4．1970 年，我国发射的第一颗人造地球卫星绕地球运动轨道近似为圆形，运行周期为 114 min，轨道的平均半径为 7 782 km。请据此估算地球的质量。

【答案】5.59 × 10²⁴ kg

5．我国发射了绕月运行的探月卫星“嫦娥一号”。该卫星在月面着陆前的轨道近似圆形，且贴近月球表面运行。已知月球质量约为地球质量的 \(\frac{1}{{81}}\)，月球半径约为地球半径的 \(\frac{1}{{4}}\)，地球的第一宇宙速度约为 7.9 km/s，该探月卫星绕月运行的速率约为多少？

【答案】1.8 km/s

6．火星的质量大约是地球的 \(\frac{1}{{9}}\)。如图所示，卫星 M 和卫星 E 分别以等大的轨道半径绕火星和地球做匀速圆周运动。哪个卫星的周期更短？请说明理由。

【答案】T = 2π\(\sqrt {\frac{{{r^3}}}{{GM}}} \)。因为地球质量大于火星质量，所以卫星 E 周期更短。

7．下表给出了五颗卫星绕木星运行的数据，这些卫星的运动可近似视为圆周运动。

（1）请根据表中数据定性描述：卫星运行周期与轨道半径之间的关系，卫星运行周期与卫星质量之间的关系。

（2）请用物理规律来证明你的上述分析。

【答案】（1）由表中数据可以看出：轨道半径越大，周期越长；卫星运行的周期与卫星的质量没关系。

（2）T = 2π\(\sqrt {\frac{{{r^3}}}{{GM}}} \)

所以，周期 T 与轨道半径的 \(\sqrt {{r^3}} \) 成正比，与卫星的质量没有关系。

8．某同学在解决一个物理问题的过程中，计算出一颗人造地球卫星绕地球做圆周运动的周期是 80 min。你觉得该同学的答案合理吗？请说明理由。

【答案】不合理。近地卫星的周期 T_min ≈ 84 min，所以人造地球卫星绕地球做圆周运动的周期是 80 min 不合理。

发布时间：2022/1/23 下午4:20:55  阅读次数：1669