第 4 章 第 1 节 天地力的综合：万有引力定律

自远古时期，人类就开始孜孜不息地探索天体的运动规律，创作了很多关于星空的神话、史诗。“仰观吐曜，俯察含章”，浩瀚宇宙中，日月星辰周而复始地运行（图 4-1），它们有着怎样的运动规律？本节将学习开普勒定律和万有引力定律。

图 4-1 茫茫星空

1．行星运动的规律

自古希腊起，人们一直以为太阳、月亮和星星都是围绕地球转动的，直到波兰天文学家哥白尼（ N. Copernicus，1473—1543）提出“日心说”。继而，德国天文学家开普勒（J. Kepler，1571—1630，图 4-2）根据前人的观测和研究，于 1609 年和 1619 年先后提出了太阳系行星运动的三大定律。

开普勒第一定律：所有行星绕太阳运动的轨道都是椭圆，太阳位于椭圆的一个焦点上（图 4-3）。图中 F₁、F₂ 是椭圆的两个焦点。

图 4-3 开普勒第一定律示意图

开普勒第二定律：任何一个行星与太阳的连线在相等的时间内扫过的面积相等（图 4-4）。

图 4-4 开普勒第二定律示意图

开普勒第三定律：行星绕太阳运行轨道半长轴 a 的立方与其公转周期 T 的平方成正比（图 4-5）。

\(\frac{{{a^3}}}{{{T^2}}}\) = k

图 4-5 开普勒第三定律示意图

科学书屋

表 4-1 八大行星绕太阳运动的有关数据

注：a 是年的单位符号。偏心率 e 是椭圆扁平程度的量度，等于椭圆两焦点间的距离与长轴长度的比值。圆是椭圆的特例，偏心率为 0。

由开普勒定律可知，行星的运行轨道为椭圆，并且其绕太阳运行的速率不断变化。由表中的数据可知，太阳系八大行星的运行轨道偏心率都小于 0.3，都可近似认为是圆形。为了便于研究问题，人们通常认为行星绕太阳做匀速圆周运动。

迷你实验室

画椭圆

请准备笔、纸、图钉和绳子，按图 4-6 所示，试画出偏心率分别为 0.9、0.5、0.1 的椭圆，由此体会把行星轨道近似看成圆形的原因。

图 4-6 根据不同偏心率画椭圆

2．万有引力定律

太阳系的行星在各自基本恒定的轨道上围绕太阳运动，并且遵循一定的运动规律。这些行星为什么会如此运转？它们为什么既不会脱离太阳，又不会坠向太阳？牛顿总结了前人的研究成果，运用开普勒三大定律和自己在力学、数学方面的研究成果，于 1687 年在《自然哲学的数学原理》一书中正式提出了万有引力定律（law of universal gravitation）：

自然界中任何两个物体都是相互吸引的，引力的方向沿两物体的连线，引力的大小与这两个物体质量的乘积 m₁m₂ 成正比，与这两个物体间的距离 r 的平方成反比（图 4-7），即

F = G  \(\frac{{{m_1}{m_2}}}{{{r^2}}}\)

式中，质量的单位用千克（kg），距离（两个物体视为质点时，r 是两质点的距离；若是两个质量分布均匀的球体， r 则是两球心的距离）的单位用米（m），力的单位用牛顿（N）。

G 为引力常量，在数值上等于两个质量都为 1 kg 的物体相距 1 m 时相互吸引力的大小。根据 2014 年国际科学技术数据委员会（CODATA）推荐的基本物理常数值，G =（6.674 08 ± 0.000 31）×10⁻¹¹ N·m²/ kg²，通常取 G = 6.67×10⁻¹¹ N·m²/kg²。

拓展一步

对万有引力定律公式的推导

如果将行星运行的轨道近似视为圆形，就可由牛顿运动定律和开普勒定律推导出万有引力定律。

设质量为 m 的某行星，以速率 v 绕质量为 M 的太阳做匀速圆周运动，它们之间的距离为 r。由牛顿第二定律可知，行星所需要的向心力

F = m \(\frac{{{v^2}}}{r}\)

将行星的运转周期 T 和速率 v 的关系式 v = \(\frac{{2\pi r}}{T}\) 代入上式并加以整理，可得

F = 4π² （\(\frac{{{r^3}}}{{{T^2}}}\)）\(\frac{{{m}}}{r^2}\)

由开普勒第三定律可知，\(\frac{{{r^3}}}{{{T^2}}}\) 是常量，因此 F 与 m 成正比，与 r² 成反比。

行星所需要的向心力由太阳对行星的引力提供。根据牛顿第三定律可知，行星与太阳间的相互引力应大小相等、方向相反、性质相同，这个引力也应与太阳的质量 M 成正比，综上所述，有

F = G  \(\frac{{Mm}}{{{r^2}}}\)

G 为引力常量，F 为万有引力，其方向在两物体的连线上。

例题

如图 4-8 所示，木星是太阳系中最大的行星，与太阳的距离为 7.8 × 10⁸ km，木星和太阳的质量分别为 1.9 × 10²⁷ kg 和 2.0 × 10³⁰ kg。试求木星与太阳之间的万有引力大小。

分析

已知两天体的质量和它们之间的距离，可用万有引力定律计算它们之间的引力。

解

由题意可知，m₁ = 1.9 × 10²⁷ kg，m₂ = 2.0 × 10³⁰ kg， r = 7.8×10¹¹ m。

根据公式 F = G\(\frac{{{m_1}{m_2}}}{{{r^2}}}\) 可得所求引力

\[\begin{array}{l}F = 6.67 \times {10^{ - 11}} \times \frac{{1.9 \times {{10}^{27}} \times 2.0 \times {{10}^{30}}}}{{{{(7.8 \times {{10}^{11}})}^2}}}\\ = 4.2 \times {10^{23}}{\rm{N}}\end{array}\]

讨论

虽然天体之间的距离很远，但由于它们的质量非常大，所以它们之间的万有引力很大。

策略提炼

天体相距很远，一般可视为质点。因此，在计算天体之间的万有引力时，可以直接运用万有引力定律计算。

在计算过程中，因数据较大，对指数的计算要特别仔细。

迁移

粗略研究行星的轨道运动时，通常只考虑太阳对行星的万有引力。木星与地球之间的最近距离约为 6.3 × 10⁸ km，地球的质量约为 6.0 × 10²⁴ kg。请估算木星与地球之间的万有引力大小，并与木星和太阳之间的万有引力大小作比较。

实际上，太阳系中的各大行星受其他天体的引力远小于受太阳的引力，它们运动状态的变化主要受太阳引力支配。虽然任何两个物体之间都有万有引力，但日常物体的质量一般较小，万有引力往往可以忽略。我们之所以能明显感觉到地球引力的作用，是由于地球的质量很大。在估算地球与物体之间的万有引力时，通常将地球质量等效集中于地球中心。

拓展一步

牛顿的月—地检验

牛顿认为，物体落地是由于地球对物体的吸引，而地球与物体间的引力可能与天体间的引力具有相同性质。他的证明思路如下（图 4-9）：

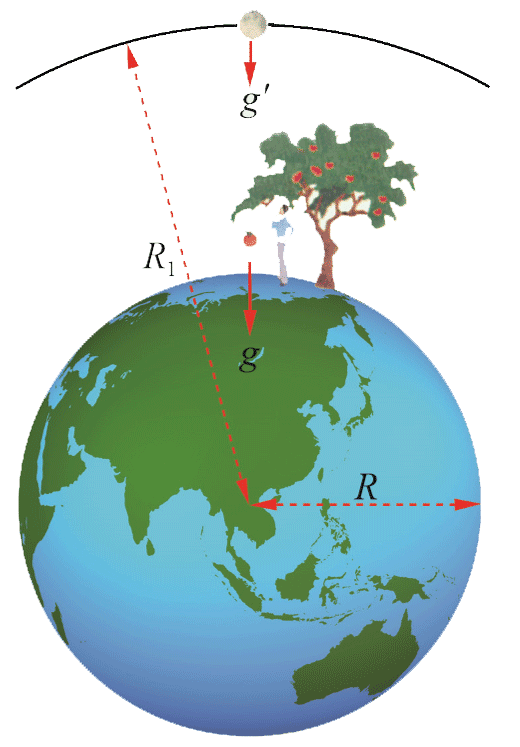
在地面上质量为 m 的物体所受的地球引力遵守万有引力定律，则有

\[F = G\frac{{Mm}}{{{R^2}}} = mg\]

式中，M 为地球质量，R 为地球半径。

因此，物体在地面处重力加速度的大小

\[g = G\frac{M}{{{R^2}}}\]

假设将地面上的物体放到月球绕地球旋转的轨道上，由于月球轨道半径 R₁ 是地球半径 R 的 60 倍，则物体受地球引力作用产生的加速度 gʹ 就是它在地面时重力加速度的 ，

\[g = \frac{1}{{{{60}^2}}}g = \frac{1}{{3600}} \times 9.8{\rm{m/}}{{\rm{s}}^{\rm{2}}} = 2.7 \times {10^{ - 3}}{\rm{m/}}{{\rm{s}}^{\rm{2}}}\]

这是根据地球对物体的万有引力计算出的处在月球轨道的物体的加速度，与月球绕地球公转的向心加速度恰好相等［已知月球绕地球公转的半径约为 3.8 × 10⁵ km，公转周期约为 27.3 d（d 是天的单位符号），请自己计算验证］。这表明地球对月球的引力与地球对地面物体的引力具有相同性质，由此说明了地球对地面物体的引力与天体之间的引力具有相同性质，遵循同样的规律。

牛顿的月—地检验，将地球对地面物体的引力、行星对卫星的引力统一起来，证明了它们都遵守万有引力定律。

3．引力常量的测定

万有引力定律是自然界的基本规律之一，在物理学中占有非常重要的地位。然而，牛顿当时未能给出引力常量的准确值，如何测量引力常量一时成为物理学界普遍关心的重大课题之一。

直到 1798 年，英国物理学家卡文迪许（H．Cavendish，1731—1810）利用扭秤实验（图 4-10），巧妙地测出了铅球间的引力，从而证明了万有引力定律的正确性，并得到了当时精确度很高的引力常量数值。

引力常量的确定有着非常重要的意义，它使万有引力定律能够广泛地应用于生产生活实践中，有了真正意义上的实用价值。卡文迪许也因此被称为“能称出地球质量的人”。

拓展一步

卡文迪许扭秤实验的原理

卡文迪许实验的原理如图 4-11 所示。当两个等质量的大铅球分别靠近两个等质量的小铅球时，大、小铅球之间的相互引力 F，使固定小铅球的支架受到力矩作用而转动，金属丝因形变而产生扭转力矩，当两个力矩平衡时支架停止转动。固定在支架上的平面镜 M 反射到标尺上的光束会转过一个小角度，由此可以推算出大、小铅球之间的引力。已知大、小铅球的质量 mʹ、m 及它们之间的距离 r，由万有引力定律便可以计算出引力常量 G 。

卡文迪许实验装置测出了非常微小的引力，从而算出了引力常量 G。你认为该装置的巧妙之处体现在哪些方面？如果你有疑惑，可以上网查找相关资料进行了解。

测定常量是科学研究的一项重要内容，是人们深入认识自然的一种方式。对科学定律中常量的测定，其精确度是不断提高的。

节练习

1．重力是因地球的吸引而产生的，请分析重力加速度 g 与哪些因素有关。进一步分析重力加速度 g 的异常变化对地下矿藏勘探工作有何价值。

【答案】重力加速度 g 值的大小主要与地球的质量和半径有关，也与海拔高度和纬度有关。在相同纬度、相同海拔处，矿藏的分布不同，导致地下的质量分布不同。如果密度较大，则该地的 g 值较大，反之g 值较小。所以，根据不同的 g 值可以分析地下的质量分布。进而判断是否有矿藏以及矿藏的大致种类。

2．在太阳系中，火星和木星沿各自的椭圆轨道绕太阳运行。根据开普勒行星运动定律可知

A．太阳位于木星运行轨道的中心

B．火星和木星绕太阳运行速度的大小始终相等

C．火星与木星公转周期之比的平方等于它们轨道半长轴之比的立方

D．在相同时间内，火星与太阳连线扫过的面积等于木星与太阳连线扫过的面积

【答案】C

3．海面上有两艘正在行驶的轮船，质量都是 1.0 × 10⁴ t，相距 10 km。它们之间的万有引力有多大？请将这个力与其中一艘轮船所受的重力进行比较，看看是重力的多少倍。

【答案】F = 6.67 × 10⁻⁵ N，\(\frac{F}{G}\) = 6.67 × 10⁻¹³

4．有一颗小行星绕太阳做圆周运动，它的轨道半径是地球轨道半径的 n 倍。这颗小行星的公转周期是多少年？

【答案】\({n^{\frac{3}{2}}}\) 年

5．曾经有人用木星的直径作为量度单位，测量了木星卫星的轨道半径。如图所示，他发现木卫一的周期是 1.8 天，距离木星中心 4.2 个木星单位，而木卫四的周期是 16.7 天。请预测木卫四距离木星中心的距离。

【答案】r₂ = 4.42r₁ = 18.56 个木星单位

6．查阅资料，写一篇关于卡文迪许实验室的科技小论文，内容包含卡文迪许实验室的发展历程和作出的主要贡献等。

【答案】略

发布时间：2022/1/22 下午4:48:15  阅读次数：2296