第四章 第五节 牛顿运动定律的应用

图 4–28 赛车
赛车是学生喜爱的一项竞技运动,包含着科技水平和工业能力的竞争。车辆的运动与牵引力、阻力、加速性能和质量紧密相关,应用牛顿运动定律分析相关问题,有助于模型建构、综合分析能力的提高。
本节以此作为切入点,引出讨论主题——牛顿运动定律的应用。
本节编写思路
本节以拔河比赛中的力学问题为载体,感受应用牛顿运动定析问题的一般思路,认识受力分析是研究力学问题的基础,体会模型建构的方法。
通过“示例”学习应用牛顿定律解决力与运动问题的解题规范,知道牛顿运动定律所能解决的两类问题。
在“自主活动”中体会用分段处理的方法,理解整体与局部的关系。
本节的学习经历将促进对牛顿运动定律的理解,引导对所学内容的总结与综合,体会模型建构、演绎推理、综合分析的作用,养成严谨、规范地处理问题的习惯。
宏观世界中,无论陆、海、空各种交通工具的运动还是火箭发射和宇宙航行,都遵循着牛顿运动定律。例如,为了使图 4–28 所示的赛车提速,不仅需要考虑动力和阻力等因素,还要为车体瘦身减重;章导图所示的航空母舰设计时不仅要考虑舰载机安全起飞,为了使舰载机在航空母舰上安全降落,还设计了拦阻索来缩短舰载机的着舰滑行距离。我们几乎时时处处都要用到牛顿运动定律去解决遇到的问题。下面将运用牛顿运动定律来分析几个事例,体会用牛顿运动定律解决问题的过程和方法。

图 4–29 进行中的拔河比赛
如图 4–29 所示,两队正在进行拔河比赛,最终左队获胜。
由于比赛的具体参与者很多,情况比较复杂,我们仅分析右队恰好被获胜的左队拉得向前滑行的情况。我们像上一节开始时一样,将情况简化为两位队员直接互拉,并将队员抽象为两个质点,分析其受力。
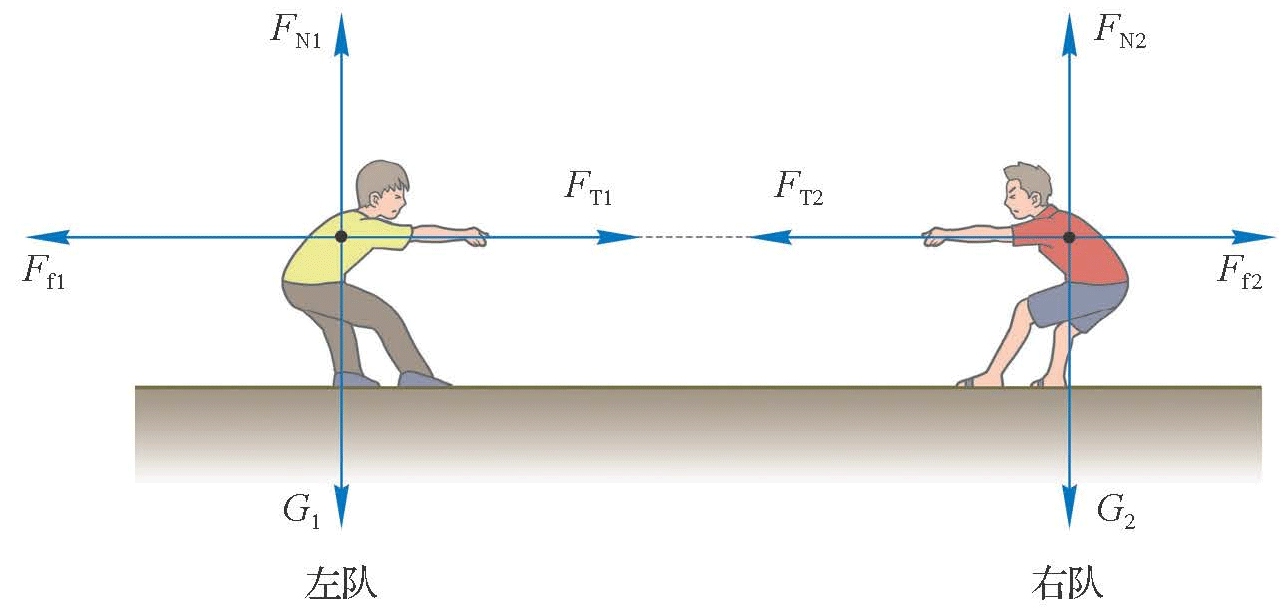
图 4–30 两队队员受力分析
根据牛顿第三定律,左、右两队间的拉力是一对作用力和反作用力,大小相等,方向相反。如图 4–30 所示,左队队员受到右队的拉力 FT1 。因此,左队队员有相对于地面向右运动的趋势,地面对左队队员有一个向左的摩擦力 Ff1。同理,可对右队队员作受力分析。
由于分析两队拔河的情况较为复杂,故将其简化为两人之间的拔河场景。即便如此,仍需做出多方面的近似。首先是假设两人之间通过直接的相互作用,把绳子视为其中一人手臂的延伸,其原因是只有这样才能认为拔河双方间的相互作用是作用力和反作用力。如果两人通过拔河绳互拉,则虽然在不可伸长轻绳的前提下两人受到绳子的拉力相等,但两人之间的相互作用并不是一对作用力与反作用力。
选择最简单的模型,将两人均视为质点,相互作用是一对作用力与反作用力,两人与地面之间的摩擦因数相等,沿水平方向发生相互作用。在此前提下通过受力分析可知,胜负并不取决于谁的力气大,而是由两人所受的地面摩擦力决定,由于摩擦因数相等,故体重大者占优。如果假设两人体重相等,但相互作用不沿水平方向而上述其他假设不变,通过简单分析可知身材高者占优。
对于获胜的左队,只要 FT1 的大小不超过其与地面间的最大静摩擦力,必有 FT1 = Ff1,左队队员所受合力为零。根据牛顿第一定律,队员保持静止状态。
对于失利的右队,其与地面间的最大静摩擦力比左队的小,小于右队所受的拉力,即 Ff2 < FT2,合力不为零,方向向左。根据牛顿第二定律,右队的加速度向左,滑向左边,从而输掉了比赛。
在本例中决定输赢的是左、右两队在水平方向所受的合力。左队之所以会赢是因为他们受到的合力为零,右队之所以会输是因为向左的合力改变了他们的运动状态。
上述实例中,我们根据两队的受力情况,运用牛顿运动定律讨论了决定拔河比赛输赢的原因。在其他情况中同样可以根据物体的运动状态变化,依据牛顿运动定律分析其受力情况。

图 4–31 运动员从雪坡上下滑

图 4–32 运动员的受力分析
示例 质量为 60 kg 的滑雪运动员不借助雪杖,从倾角为 30° 的斜坡上自静止起沿斜坡向下加速滑行(图 4–31),滑行 200 m 通过标志杆时的速度大小为 40 m/s。估算滑雪运动员所受的阻力。(g 取 10 m/s2)
分析:把滑雪运动员抽象为质点,把情境转化为示意图,分析运动员的受力情况。根据运动员的运动情况,分析加速度,按需要建立坐标系,运用牛顿运动定律和运动学规律求解。
解:以运动员为研究对象,画出运动员从雪坡上下滑的受力分析,如图 4–32 所示。
已知运动员的质量 m = 60 kg,则运动员受到的重力为
\[G = mg = 60 \times 10{\rm{N}} = 600{\rm{N}}\]
运动员的下滑过程可视为初速度为零的匀加速直线运动,加速度 a 沿斜面向下。以沿斜坡向下为正方向,
则运动员的初速度 vA = 0 m/s,末速度 vB = 40 m/s,位移 xAB = 200 m,由运动学规律可得
在前面课程中,曾经强调物理量有相应单位,因此在代入数据进行计算时,需同时写出数值和单位。但通过第三节单位制的讨论可知,如果在代入数据前已经把所有物理量的单位以 SI 表示,那么最后结果一定也是由 SI 表示的单位,在这种情况下,就不必逐一写出每个物理量的单位而只要写出最后结果的 SI 单位。以后的计算书写均按此规范即可。
\[v_B^2 - v_A^2 = 2a{x_{AB}}\]
\[a = \frac{{v_B^2 - v_A^2}}{{2{x_{AB}}}} = \frac{{{{40}^2} - 0}}{{2 \times 200}}\;{\rm{m/}}{{\rm{s}}^{\rm{2}}} = 4\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}\]
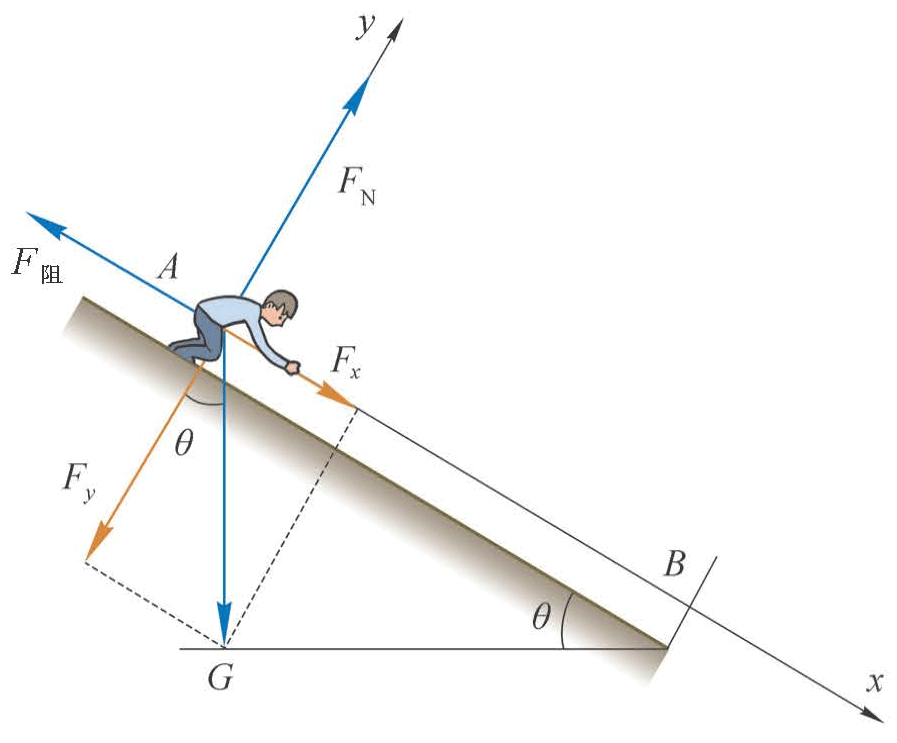
图 4–33 沿 x、y 方向分解重力
运动员的加速度 a = 4 m/s2,方向沿斜坡向下。
根据牛顿第二定律,运动员所受的合力也沿斜坡向下,垂直于斜坡方向上的合力为零。取 x 轴平行于斜坡向下,取 y 轴垂直于斜坡向上,建立坐标系。沿 x 与 y 方向分解重力,如图 4–33 所示。
\[\begin{array}{l}{F_x} = G\sin \theta \\{F_y} = G\cos \theta \end{array}\]
沿 x 方向的合力使运动员沿斜坡向下加速运动,根据牛顿第二定律得
\[\begin{array}{l}{F_x} - {F_阻} = ma\\{F_阻} = {F_x} - ma\end{array}\]
\(\begin{array}{l} = G\sin \theta - ma\\ = (600 \times 0.5 - 60 \times 4){\rm{N}}\\ = 60{\rm{N}}\end{array}\)
滑雪运动员所受的平均阻力为 60 N,方向沿斜坡向上。
在本示例中,我们先根据运动员的运动情况求出他的加速度;再运用牛顿运动定律确定运动员的受力情况。有时我们也会运用牛顿运动定律根据物体的受力来确定物体的运动情况。这两种类型的应用都是人们认识客观世界、进行科学研究的重要途径。
当我们坐过山车加速上升时,会感到人被紧紧地压在座椅上不能动弹;而当过山车加速向下俯冲时,则又会有悬空感。如果你仔细体会,乘电梯上、下楼的过程中也会有类似感受。这些感受都与“超重”和“失重”现象有关。
测量体重时,人对秤的压力与人所受的重力大小相等。但是,如果人在秤上突然下蹲或突然起立,秤的示数就会发生改变。手持悬挂重物的细线并保持重物静止时,线上的拉力大小等于重物所受的重力大小。若手突然加速上提,细线可能会断裂,说明线上的拉力
图 4–34 电梯从底楼上升到顶楼过程力传感器示数随时间的变化
在细线断裂前变大了。这些现象都与竖直方向的运动有关。让我们通过实验来研究。
当物体在地球表面沿竖直方向做加速或减速运动时,就会发生超重或失重现象。超重和失重现象的产生与物体的运动速度无关,仅取决于物体的加速度,且发生超重与失重现象时物体所受到的重力并不发生变化。超重与失重现象可总结如下:
|
运动情况 |
超重、失重情况 |
视重 |
|
匀速运动 |
无 |
mg |
|
加速度竖直向上,大小为 a |
超重 |
mg + ma |
|
加速度竖直向下,大小为 a |
失重 |
mg − ma |
|
加速度竖直向下,大小为 g |
完全失重 |
0 |
在电梯顶板上固定一个力传感器,将重物挂在力传感器的挂钩上。当电梯静止时通过力传感器测得的示数即为重物对力传感器拉力的大小,与重物所受重力 G 的大小相等。电梯从底楼由静止起上升,最后停在顶楼。重物对传感器拉力大小在此过程中随时间的变化如图 4–34 所示。
电梯上升过程中经历了先加速后匀速再减速的运动过程。在电梯加速上升的过程中,重物对力传感器的拉力大于重物所受的重力;在电梯减速上升的过程中,重物对力传感器的拉力小于重物所受的重力;在电梯匀速上升的过程中,重物对力传感器的拉力大小等于重物所受的重力。物体对悬绳的拉力或对支持物的压力大于物体所受重力的现象,称为超重(overweight)现象。物体对悬绳的拉力或对支持物的压力小于物体所受重力的现象,称为失重(weightlessness)现象。
如果一个人站在电梯中,当发生超重或失重现象时,电梯地板对他的作用力大小就等于视重大小。爱因斯坦提出了这样一个思想实验:如果在远离所有天体的宇宙深处,航天员处于一个密闭的太空舱中,太空舱以大小为 g 的加速度向上加速运动,此时航天员所受太空舱地板对他的作用力大小为 mg。由于航天员并不知道太空舱的运动情沉,因此他可以认为这是因为太空舱在向上以大小为 g 的加速度做加速运动;也可以认为太空舱是静止在一个重力加速度为 g 的星球表面,他受到了星球引力的作用。这就出现一个问题,虽然在两种情况下航天员都会发现地板对他的作用力是 mg,但如果是前一种情况,m 是惯性质量,而如果是后一种情况,m 是引力质量。由于惯性质量与引力质量相等,因此在航天员看来,受到引力和具有加速度两者是等价的。爱因斯坦从惯性质量与引力质量相等出发,在分析思考了引力和惯性的关系后提出了广义相对论的等效原理(弱等效原理):不能在局部区域内分辨力是由加速度产生的还是由物体产生的,在局域范围内加速场与引力场等价。
根据图 4–34 所示的 F–t 图像大致画出电梯上升过程的 v–t 图像,并说明你的作图依据。
“自主活动”需要学生对电梯中的重物受力分析,运用牛顿第二定律,根据图 4–34 逐段分析重物的加速度,画出大致的 v–t 图像。这是用多段运动的 v–t 图像展示比较复杂的运动过程,也是牛顿运动定律的应用。
牛顿三大运动定律是牛顿力学的基础。在我们的生活、生产和科学实践中,无论是大楼、桥梁及太空站的结构,还是汽车、飞机、火箭、人造卫星及各种天体的运动,或是岩石、地壳、洋流、大气等的移动,都遵循牛顿力学规律。
牛顿系统总结了伽利略、开普勒(J.Kepler,1571—1630)和笛卡尔等人的研究成果,以实验为指导,利用伽利略开创的观测与数学分析相结合的方法,才在前人工作的基础上提出了牛顿运动定律。所以,一个规律的发现不可能只经过几次简单的实验就得以实现。科学家们要搜集已有的实验事实,在此基础上归纳出某一规律。这一过程既需要谨慎的态度、求实的作风,也需要勇气和信念。
300 多年前建立的牛顿力学至今在人类的生活、生产和科学实践中依然发挥着重大作用。牛顿力学中所建立的许多基本概念、基本规律和基本方法都已经推广到物理学的其他领域和其他学科。牛顿力学可以说是人类历史上建立的第一个重要的科学理论。科学家们通过建立一套基本观念、基本概念,以及定律、公式等,对复杂的自然现象作出解释,充分体现了人类的智慧。
- 磁浮列车是连接上海浦东国际机场的重要交通工具之一,列车运行最高速度为 430 km/h。若列车从车站开出后可视作匀加速直线运动,经过 4 min 就可达最高速度。求一位质量为 60 kg 的乘客在列车加速过程中受到的合力有多大?
- 质量为 m 的木块放置于粗糙的水平桌面上。若用大小为 F 的力水平拉木块,其加速度为 a1;当拉力方向不变,大小变为 2F 时,木块的加速度为 a2。试写出 a1 与 a2 的关系,并比较两者的大小。

图 4–35
- 如图 4–35 所示,一个质量为 0.15 kg 的棒球被球员接住的过程中,速度会在大约 0.05 s 内从 30 m/s 骤减到 0,作用在这个棒球上的力约为多大?方向如何?
- 滑板运动员在斜坡上练习。他从倾角为 θ 的斜坡底端携带滑板以加速度 a 由静止开始沿直线向上“奔跑”;经时间 t 后,突然双脚站立在滑板上,继续上滑;最后沿原路退滑到出发点。这是他完成的一次练习。这样一次练习过程可以分为哪几个阶段?说说你分段的依据。

图 4–36
- 图 4–36 所示为在飞行中的大型客机内进行失重训练的中国航天员。他们正处于接近完全失重的状态。说一说此时客机的运动状态。
- 某人在地面上最多能举起 60 kg 的物体,而在一个加速下降的电梯里最多能举起 80 kg 的物体。(g 取 10 m/s2)
(1)求电梯的加速度。
(2)若电梯以此加速度上升,此人在电梯里最多能举起物体的质量是多少?
问题与思考解读
1.参考解答:合力约为 30 N
命题意图:根据运动求合力。
主要素养与水平:模型建构(Ⅰ);科学推理(Ⅱ)。
2.参考解答:a1 = \(\frac{{F - f}}{m}\),a1 = \(\frac{{2F - f}}{m}\),因此,a2>2a1
命题意图:对相似的情境进行比较。
主要素养与水平:科学推理(Ⅱ)。
3.参考解答:约为 90 N,与棒球运动速度方向相反
命题意图:简单建模,从运动求力。
主要素养与水平:模型建构(Ⅰ);科学推理(Ⅱ)。
4.参考解答:跑动阶段和滑行阶段;依据是受力情况不同。或:跑动阶段、上滑阶段和下滑阶段;依据是受力情况、运动规律不同(注:分段方式与分段依据要对应)
命题意图:运动的分段分析。
主要素养与水平:科学推理(Ⅱ);科学论证(Ⅱ)。
5.参考解答:以加速度 g 减速上升或加速下降
命题意图:通过实际事例理解超重和失重。
主要素养与水平:运动与相互作用(Ⅰ);科学推理(Ⅱ);社会责任(Ⅰ)。
6.参考解答:(1)某人在地面上最多能举起 60 kg 的物体,此人的最大举力为 F = mg = 60×10 N = 600 N,则加速下降的电梯中,根据牛顿第二定律,得 mg − F = ma,解得a = \(\frac{{mg - F}}{m}\) = \(\frac{{800 - 600}}{{80}}\) = 2.5 m/s2
(2)若电梯加速上升,根据牛顿第二定律,得 F − mʹg = mʹa,解得 mʹ = \(\frac{F}{{g + a}}\) = \(\frac{{600}}{{10 + 2.5}}\) kg = 48 kg
命题意图:从实际问题中提取研究对象和运动过程。
主要素养与水平:模型建构(Ⅰ);科学推理(Ⅱ)。
发布时间:2021/7/15 下午5:31:47 阅读次数:8110
