第三章 相互作用与力的平衡 小结
- 基本概念和基本规律
力:物体与物体之间的相互作用。
重力:物体在地面附近由于地球的吸引而受到的力。重力的大小 G = mg,方向竖直向下,作用点在物体的重心。
弹力:发生弹性形变的物体由于要恢复原状而对引起形变的物体施加的作用力。
胡克定律:在弹性限度内,弹簧发生弹性形变时弹力的大小 F 跟弹簧形变量 x 成正比,即 F = kx。
滑动摩擦力:两个相互接触的物体发生相对运动时在接触面上产生阻碍相对运动的力。其大小跟压力成正比,Ff = μFN,μ 是动摩擦因数,与接触面的材料、粗糙程度等因素有关。
静摩擦力:两个相互接触的物体具有相对运动趋势时在接触面上产生阻碍相对运动趋势的力。
合力和分力:当物体受到几个力同时作用时,可以用一个力来替代这几个力,产生与原来几个力作用相同的效果。这个力就称为合力,原来的几个力是这个合力的分力。求几个力的合力的方法称为力的合成。把一个力用几个力同时作用来替代的方法称为力的分解。力的合成和分解都遵循平行四边形定则。
- 基本方法
通过探究实验,感受实验与推理相结合的物理学研究方法。
在探究力的合成规律实验中,认识等效替代方法。
在探究共点力平衡条件的过程中,运用演绎、推理的方法。
- 知识结构图
图 3–53
- 体操运动员可以双臂悬挂在单杠上,也可单臂悬挂,说明两种悬挂方式中的等效替代关系。双臂悬挂时,运动员受到的拉力可简化为图 3–53 中的共点力 F1、F2 ,大小均为 500 N。试用力的图示画出这两个力的合力。
- 用大拇指和食指捏着一个装有半瓶水的开口向上的瓶子,保持静止。此时瓶子受到了哪些力的作用?不断地向瓶子里加水,直至瓶子充满水,整个过程中瓶子没有下滑。在此过程中,瓶子受到的各个力的大小是如何变化的?
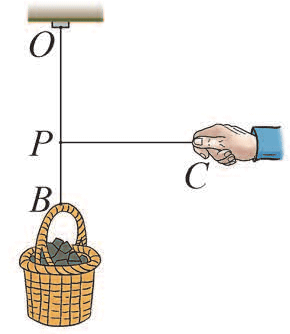
图 3–54
- 如图 3–54 所示,用绳在 O 点悬挂一个重 100 N的物体,绳 OB 能够承受的最大拉力为 200 N。若在绳上 P 点系上相同的绳 PC 后,缓慢地沿水平方向拉绳 PC,使 OP 逐渐偏离竖直方向。说明在此过程中 OP、PB 和 PC 段绳受到的拉力大小如何变化。哪一段绳可能先断裂?断裂时 OP 与竖直方向的夹角多大?
- 如图 3–55 所示,一位质量为 55 kg 的登山运动员借助安全绳稍事休息。他的左脚接触岩石,水平向左将自身推离岩面,此时安全绳与竖直方向的夹角为 20°。有人估算出绳子上的拉力约为 600 N,试写出分析推理的过程。

图 3–55
图 3–56
- 如图 3–56 所示,气球被细绳拴在地面上。无风时,细绳处于竖直状态;当风从右方水平吹来时,细绳偏离竖直方向。风越大,细绳与竖直方向的夹角越大。某同学根据这一现象尝试测量水平风力的大小,他用力传感器测出细绳上的拉力 F ,用量角器量出绳与竖直方向的夹角 α 。他如何从测得的数据得到风力 F风 的大小?写出推理的过程。
- 如图 3–57(a)所示为便利的运输工具——双轮小车。送水员用双轮小车运送 19 L的桶装矿泉水,图 3–57(b)为小车装水后的截面示意图,在拉运过程中,
图 3–57
图示角度保持不变,不计桶与小车之间摩擦力的影响。
(1)试分析送水员拉动小车使矿泉水桶和小车一起水平向右匀速运动时,矿泉水桶的受力情况,并分别求出小车 OP、OQ 侧面对桶的支持力大小。
(2)若送水员改变小车的角度,侧面 OP 与水平方向的夹角变大,侧面 OP、OQ 对桶的支持力会如何变化?
- 如图 3–58 所示,分别用 a、b、c 三根长度不同的轻绳提起装有等量清水的水桶后保持静止。某同学认为无论选用哪根轻绳,保持静止时人对绳的作用力均相等,绳上的弹力大小也相等。这一说法是否合理,简述理由。
图 3–58
图 3–59
- 如图 3–59 所示,质量为 30 kg 的小孩坐在 10 kg 的雪橇上,一成年人用与水平方向成 37° 角、大小为 100 N 的拉力拉雪橇,使雪橇沿水平地面做匀速运动。(g 取 10 m/s2,sin37° = 0.6,cos37° = 0.8)求:
(1)雪橇对地面的压力。
(2)雪橇与水平地面间的动摩擦因数。
图 3–60
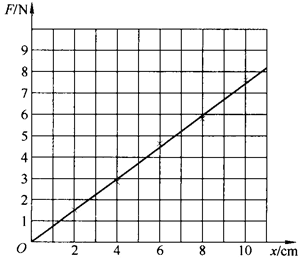
- 用如图 3–60(a)所示的实验装置研究弹簧的弹力与形变量之间的关系。轻弹簧上端固定一个力传感器,然后固定在铁架台上。当用手向下拉伸弹簧时,可从力传感器得到弹簧的弹力。用刻度尺测量弹簧原长和伸长后的长度,从而确定伸长量。测量数据如表 3–2 所示。
表 3–2
|
伸长量 x/×10−2 m |
2.00 |
4.00 |
6.00 |
8.00 |
10.00 |
|---|---|---|---|---|---|
|
弹力 F/N |
1.50 |
2.93 |
4.55 |
5.98 |
7.50 |
以弹簧的伸长量 x 为横坐标,弹力 F 为纵坐标,在图 3–60(b)中的坐标纸上画出反映弹力与伸长量关系的图线.并根据图线得出该弹簧的劲度系数。实验过程应遵循哪些注意事项?
图 3–61
- 某组同学在水平放置的方木板上做“探究两个互成角度的力的合成规律”实验。
(1)该组同学用坐标纸记下了橡皮筋的结点位置 O 以及两个弹簧测力计拉力的大小和方向,如图 3–61 所示,图中每一小格边长均代表 0.5 N。试在图中作出 F1 与 F2 的合力。
(2)改正下列实验操作中的错误。
A.先在白纸上描一个点 O ,再用两个弹簧测力计将结点拉到该位置。用手按住结点,记录力的大小和方向。
B.为了读数方便,将弹簧测力计压在木板上。
C.为了避免摩擦力的影响,斜向上拉弹簧测力计。
D.用两个弹簧测力计拉细绳时,橡皮筋结点没有与事先标记的 O 点重合,仅需调整一个弹簧测力计的大小与方向。
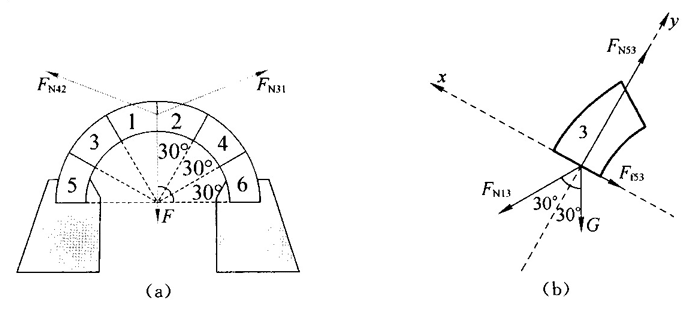
- 拱桥是古代能工巧匠的杰作,我国古代的赵州桥就是其中的典型代表。拱桥是由许多楔形砖块砌成的。为简化研究,如图 3–62 所示,将拱桥视为由 6 块相同的砖砌成的结构。如果不计砖块间摩擦力,该拱桥模型能否保持平衡?
图 3–62
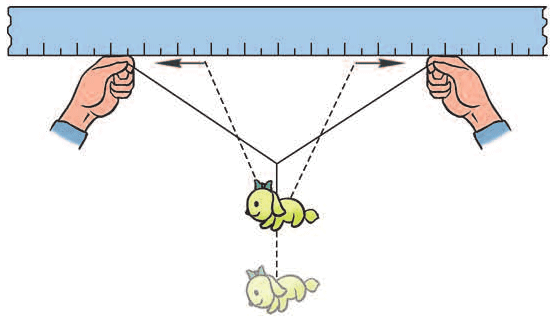
图 3–63
- 某同学设计了一个测量一根细线(或头发)能承受多大的力的实验方案。如图 3–63 所示,在一根长度已知的细线的中央悬挂着质量已知的重物,然后沿着刻度尺将双手慢慢分开,观察分开到什么距离时线断,这样就可计算细线能承受的最大拉力。试简述该同学的实验原理,并尝试做一做,提出改进的建议。
- 事物往往具有两面性,摩擦现象也概莫能外。试写一篇 200 字左右的短文,从我们熟悉的生活现象中选取不同事例,谈谈摩擦力的作用和利弊。
问题与思考解读
1.参考解答:单臂悬挂时受到单杠的作用力与双臂悬挂时受到的作用力的合力相等。按规范的力的图示画出 F1、F2,作平行四边形,获得对角线。量得对角线长度,再按比例得到合力的大小,合力大小为 500 N,图略
命题意图:培养规范作图的习惯,体会空间对称性。
主要素养与水平:模型建构(Ⅰ);科学推理(Ⅰ)。
2.参考答案:通常我们将水和瓶子作为一个整体进行分析。瓶子和水受到重力、两根手指的压力、接触处的静摩擦力。随着瓶内水量逐渐增加,瓶子与水所受的重力增加,静摩擦力也增加,手对瓶子的压力可能变化也可能不变
命题意图:对生活中的实例做受力分析。
主要素养与水平:模型建构(Ⅱ);科学推理(Ⅱ);科学态度(Ⅰ)。
3.参考解答:PB 段拉力大小不变,OP 段拉力变大,PC 段拉力变大。夹角为 60° 时,OP 段断裂
提示:以 P 点为对象,用共点力的平衡分析三个力之间关系的动态变化过程
命题意图:从静态的问题推广到多个力准静态变化的过程,了解表示力的几何图形中变与不变的意义。
主要素养与水平:科学推理(Ⅱ)。
4.参考解答:以运动员为研究对象,他受到重力、绳子的拉力和岩石的作用力,其中岩石的作用力水平向左。运动员的受力分析如图所示,根据共点力平衡的条件,绳子拉力与岩石作用力的合力竖直向上,大小等于运动员所受的重力。故绳子拉力大小 FT = \(\frac{G}{{\cos 20^\circ }}\) = \(\frac{{55 \times 9.8{\rm{N}}}}{{0.94}}\) = 573.4 N。因此,估算值 600 N 接近真实情况
命题意图:根据共点力平衡条件对实际问题做出估算。
主要素养与水平:模型建构(Ⅱ);科学推理(Ⅱ)。
5.参考解答:把有风时测得的绳子拉力分解为水平和竖直两个分力,根据水平方向二力平衡得到风力的大小为F风 = Fsinα
命题意图:利用正交分解处理物体平衡问题。
主要素养与水平:科学推理(Ⅱ);解释(Ⅱ)。
6.参考解答:(1)不计摩擦力的影响,桶受到重力和两个弹力(支持力)的作用。若 g 取 10 m/s2,OP 对桶的支持力为 152 N,OQ 对桶的支持力为 114 N
(2)因为 OP 始终与 OQ 垂直,可以利用圆的性质。若 OP 与水平面的夹角变大,OP 对桶的支持力变小,OQ 对桶的支持力变大
命题意图:引导学生将立体图转化为平面图,利于问题的分析。
主要素养与水平:模型建构(Ⅱ);科学推理(Ⅱ)。
7.参考解答:将桶和绳子视为对象,保持静止时,人对桶的作用力竖直向上,与桶所受的重力平衡。因此,无论选择哪一根绳子,人对桶和绳的整体作用力均相同。以人与绳的接触点为对象,该点受三个力。保持静止时,绳子越短,夹角越大,绳上的张力越大
命题意图:在同一个情境中,选择不同的对象进行分析。
主要素养与水平:科学推理(Ⅱ);科学论证(Ⅰ);质疑创新(Ⅰ)。
8.参考解答:以小孩和雪橇为对象,其受力情况如图所示。由于其做匀速直线运动,合力为零,沿水平方向和竖直方向正交分解,在两坐标轴方向上各分力的合力均为零。
(1)竖直方向:Fsinθ+FN = mg,解得 FN = mg – Fsinθ = 340 N。由牛顿第三定律得雪橇对地面压力:FʹN = FN = 340 N
(2)水平方向:Fcosθ – Ff = 0,Ff = μFN。解得:μ ≈ 0.24
命题意图:应用正交分解的方法。
主要素养与水平:模型建构(Ⅱ);科学推理(Ⅱ)。
9.参考解答:F–x 关系图像如图所示,在图中直线上读取相距较远两点的数据,由 k = \(\frac{{\Delta F}}{{\Delta x}}\) 得到该弹簧的劲度系数约为 74 N/m(71~77 N/m 均可)。在实验过程中应注意:(1)弹簧的拉伸长度不能超过其弹性限度;(2)拉力应保持竖直方向向下,如用钩码代替手拉等;(3)需待力传感器示数稳定后再读数
命题意图:重温测量弹簧的劲度系数实验。
主要素养与水平:证据(Ⅱ);解释(Ⅱ)。
10.参考解答:(1)如图所示。由方格纸的格数能够确定力的大小为3 N
(2)A.结点应处于自由状态。B.弹簧测力计的形变方向要与细绳方向沿同一直线。C.两个力构成的平面应与木板平面平行。D.调整一个弹簧测力计必然会影响另一个测力计的大小和方向
命题意图:来自学生的实际操作,通过完善操作步骤来反思实验过程。
主要素养与水平:质疑创新(Ⅰ);证据(Ⅱ);科学态度(Ⅰ)。
11.参考解答:将 1、2 两块砖合起来看作一个整体进行研究,如果不计其他砖块之间的摩擦,其受力情况如图(a)所示;由于其静止,合力为零。设每一块砖重 G,可得 FN42 = FN31 = 2G,再以砖 3 为研究对象,如果不计摩擦,其受力情况如图(b)所示,运用正交分解法,对第3块砖进行受力分析。因 FN13 与 FN31 互为反作用力,所以 FN13 = FN31 = 2G,FN53 = FN13cos30°+Gcos30° = \(\frac{{3\sqrt 3 G}}{2}\),FN13 及 G 在 x 轴上的合力 Fx 为:Fx = FN13sin30° − Gsin30° = \(\frac{G}{2}\),因Fx ≠0,故第3块砖不能保持平衡,而是沿其所受合力方向滑出。从总体上看,拱桥的结构不能保持平衡,第 3、4 块砖会沿与第 5、6 块砖的接触面斜向上滑出,而第 1、2 块砖又会因第 3、4 块砖的滑出而下陷,致使结构塌毁,石块之间必须有摩擦力作用。查表可知,石块间的摩擦因数大于 0.5,根据计算,完全满足石拱桥设计要求。在此基础上,也可在石块之间加混凝土
命题意图:根据共点力平衡条件,通过建模分析解决实际问题。
主要素养与水平:科学推理(Ⅱ);科学论证(Ⅲ);社会责任(Ⅰ)。
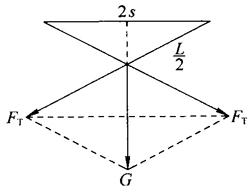
12.参考解答:实验中缓慢移动细绳两端至断裂时测量细绳两端距离 2s,受力分析如图所示。由几何关系 \(\frac{{{F_T}}}{{\frac{G}{2}}}\) = \(\frac{{\frac{L}{2}}}{{\sqrt {{{\left( {\frac{L}{2}} \right)}^2} - {s^2}} }}\),得FT = \(\frac{{GL}}{{2\sqrt {{L^2} - 4{s^2}} }}\)。实验中可能会出现的问题:手拉细线时细线与手指间可能会发生滑动
命题意图:用共点力平衡的条件来解决一个真实的问题,通过体验对原有的方案进行反思。
主要素养与水平:质疑创新(Ⅰ);证据(Ⅱ);科学态度(Ⅰ)。
13.参考解答:从摩擦力的利、弊两个角度阐述。可以选取诸如行走、搬运、传动等常见现象讨论,分析其中摩擦力的方向和作用。提示:也可以设想如果摩擦力消失,日常生活中习以为常的现象会发生怎样的变化
命题意图:根据摩擦力的概念和规律,列举生活实例并分析解释摩擦力在其中发挥的作用。
主要素养与水平:运动与相互作用(Ⅰ);科学论证(Ⅰ);科学本质(Ⅰ)。
发布时间:2021/7/13 下午8:59:11 阅读次数:5923
