第三章 第三节 力的分解

图 3–29 学生拉着轮胎前进
用学生拉轮胎进行负重跑为理解力的分解提供情境基础。通过课堂讨论可更好地理解力的分解依据和意义。
本节以此为例引出拉力的两个作用效果,与后续按效果分解力的讨论相呼应。
本节编写思路
本节首先从力的矢量合成方法出发,讨论了分解力的一般方法。通过推理论证,感悟数学手段是分析问题的一般方式。在“自主活动”中,亲身体验力的分解效果,并对“分力小于合力”的潜意识造成矛盾冲突。通过拉车出泥沼的情境形成在实际问题中需根据效果分解力的认识,理解力的分解的基本原则,通过“示例”了解利用力的分解解决问题的一般方法。
经历根据实际效果进行力的分解的过程有助于加深对力的分解是力的合成的逆过程的理解,形成利用作图、计算等方法进行力的分解的技能,促进科学推理能力的发展,也为后续力的正交分解打下基础。
如图 3–29 所示,学生用绳拉着轮胎进行负重跑以训练体能。学生对轮胎的拉力 F 是斜向上的。这个力产生了两个效果:一方面使轮胎克服阻力前进,另一方面把轮胎向上提。这相当于两个力同时作用在轮胎上:一个是水平方向的力 F1,使轮胎前进;一个是竖直方向的力 F2,把轮胎向上提。F 与 F1、F2 的共同作用效果相同,可以用 F1 和 F2 来替代 F。
这种把一个力用几个同时作用的力来替代的方法称为力的分解(decomposition of force)。力的分解也是一种等效替代。
图 3–30 一个力可以
有无穷多种分解方法
一个力可以由任意多个分力来替代。我们针对一个力分解为两个分力的简单情况分析。
力是矢量,力的合成遵循平行四边形定则。力的分解同样遵循平行四边形定则。
根据平行四边形定则,以一个力 F 为对角线作出平行四边形;平行四边形的两条邻边即为与 F 共点的两个分力。如果没有限制,对于同一条对角线,可以作出无穷多个平行四边形(图 3–30)。因此,一个力分解为两个分力的分解方法可以有无穷多种。
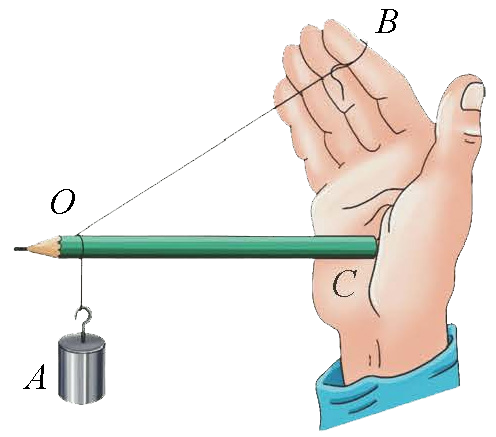
图 3–31 钩码对 O 点的拉力的作用效果图
用铅笔、细线把一个钩码按如图 3–31 所示的方式悬挂起来,谈谈悬挂钩码后手指和手掌有什么感受。根据感受,谈谈可以沿哪两个方向分解钩码对 O 点的拉力,你为什么这样分解?用作图法画出这两个力。
这个“自主活动”是一个利用随身物件动手做的小实验,通过动手实验,可以直观感受悬挂重物产生的竖直向下的拉力(在保持平衡的条件下,该拉力与重物的重力大小相等)分别对细线和笔杆产生的作用效果,从而将拉力分解到其产生效果的两个方向。

图 3–32 司机将汽车拉出泥沼
图 3–33 将 F 分解为 FA、FB
图 3–34 斜面上木箱所受重力的
分解
在实际问题中我们常常根据力的实际作用效果来确定分力的方向,再用平行四边形定则求出分力。
如图 3–32 所示,一辆货车陷入了泥沼无法依靠自身的动力脱身。有经验的司机会在附近找一棵结实的大树,用钢索将车 A 与大树 B 连接,拉紧;然后,司机只要将一根绳子绕过钢索中央的 O 点,沿着垂直于钢索的方向拉绳;仅需一两人之力,就能让车前进一些。收紧钢索后再拉,重复多次,就能将车拉出泥沼。司机以力 F 拉绳,有使钢索沿着 AO、BO 方向伸长的效果。将 F 沿这两个方向分解得到如图 3–33 所示的平行四边形。由图中力的矢量关系可知,由于拉力 F 几乎与钢索垂直,两个分力的夹角 α 接近 180°,人只需要施加一个不太大的力,就可以通过钢索对汽车产生很大的拉力,从而将车拉动。
示例 把一个木箱放在倾角为 θ 的斜面上,木箱受到重力的作用。从力的作用效果来看,应该怎样分解重力?分力的大小与斜面的倾角有什么关系?
分析:重力的作用产生了两个效果:使木箱有沿斜面下滑的趋势和使木箱紧压斜面。因此,木箱的重力可分解为平行于斜面向下的力 F1 和垂直于斜面向下的力 F2。
解:以木箱为研究对象,根据木箱所受重力产生的效果画出分解重力 G 的平行四边形,如图 3–34 所示。由几何关系可知
\[\begin{array}{l}{F_1} = G\sin \theta \\{F_2} = G\cos \theta \end{array}\]
F1 和 F2 的大小都与斜面的倾角有关,倾角 θ 越大, F1 越大、 F2 越小。
《说文解字注》上说“梁之字,用木跨水,则今之桥也”,“凡独木者日杠,骈木者日桥”。我国建设桥梁的历史悠久。在山东省发现了春秋战国时期齐国都城宽达七八米的护城河修桥的遗迹;在陕西省,渭河的老河床下也发现了秦昭王时期修建的渭水桥的木桩基础。许多古老的桥梁至今被保存了下来(图 3–35):建于隋朝、距今大约 1 400 年,世界上现存最早、保存最完整的古代单孔敞肩石拱桥——赵州桥;北宋年间建成的,我国现有最早的跨海大桥——洛阳桥;始建于南宋,被著名桥梁专家茅以升誉为“世界上最早的启闭式桥梁”——广济桥;建于南宋,被《马可·波罗游记》记载的,名扬海外的石造联拱桥——卢沟桥。它们既是中华民族历史文化遗产,也是世界人类科技文化的重要组成部分。
“STSE”介绍了各种桥梁。建造水上桥梁时,为了让桥下能顺利通行大型船只,桥孔下必须留有足够的净空高度,这样就必须把桥造得高一些。桥造高了,就需要引桥来连接两岸和正桥。
当汽车沿引桥上桥时,跟“示例”的分析同理,汽车所受的重力会产生沿引桥桥面向下的作用效果,即分力 F1 = Gsinθ,阻碍汽车向上行驶。为减小该阻力,需要减小引桥的倾角 θ,使引桥的坡度比较平缓。在正桥高度一定的情况下,则需要把引桥建得很长。如果将引桥建造成螺旋形,盘旋而上,则既可以保持引桥坡度的平缓,又可以节省引桥在岸边的占地,提高土地的利用率。如图所示,上海南浦大桥浦西段引桥就采用了这样的设计。


图 3–35 中国古代四大名桥
新中国成立以来,我国的桥梁建设事业飞速发展。以前的长江天堑,如今已成为平坦通途;一座座大桥横跨峡谷,其中连接云、贵两省的北盘江大桥(图 3–36)其桥面离水面有 565 m 的高度,相当于 200 层楼高,是世界第一高桥;跨海大桥,如东海
大桥、杭州湾跨海大桥、青岛海湾大桥相继建成。2018 年 10 月,世界上最长的跨海大桥,连接香港、珠海和澳门的港珠澳大桥建成通车。港珠澳大桥全长 55 km,其中跨海段 42 km,拥有世界最长的沉管隧道,是世界上最长的钢结构桥梁。

图 3–36 北盘江大桥
图 3–37 斜拉桥原理示意图
每一座桥梁均涉及力的合成、分解与平衡。
在现代桥梁建设中,斜拉桥已成为桥梁的主流。斜拉桥是将桥的主梁用许多根拉索直接系在桥塔上的一种桥梁。左右对称的斜拉索对桥塔产生一对对沿着拉索方向的拉力,每一对拉力的合力均竖直向下作用于桥塔下的桥墩(图 3–37)。斜拉桥桥体矫健轻盈,似长虹卧波,具有跨径大、桥塔高、结构稳定性强等特点。
斜拉桥是一种自锚式体系。在教材图 3–37 中,斜拉桥主梁的总重,除了被桥塔和水下墩台支撑外,还由桥塔引出的斜拉索下端的竖直分力承受。斜拉索下端的水平分力由主梁承受。斜拉索上端的拉力,左右对称地形成向下的合力,作用于桥塔和水下墩台。
了解斜拉桥中有关力的分解、合成等力学原理,可以进一步感悟科学、技术与社会的关系。
我国的桥梁建设发展日新月异,建成的大桥包揽当今世界全部桥型。中国桥梁建设已成为中国制造的亮丽名片。
- 如图 3–38 所示,一个 15 N 的力沿 OA 方向,它的一个分力沿 OB 方向,大小为 6 N。作图表示另一个分力的大小和方向。
图 3–38
- 将一个大小等于 20 N 的力,分解为两个力,其中一个分力的大小为 16 N,另一个分力的大小为 12 N。作图分析,说明满足上述条件有几种可能性。
- 如图 3–39 所示,一人通过箱带拉着一个旅行箱前进。拉力大小为 12 N,箱带与水平面夹角为 30°,求拉力的水平分力和竖直分力的大小。

图 3–39
图 3–40
- 如图 3–40 所示,光滑斜面上物体受到的重力 G 被分解为 F1、F2 两个力。判断下列说法是否正确,并简述理由。
(1) F1 是斜面作用在物体上使物体下滑的力,F2 是物体对斜面的压力。
(2)物体受到 G、FN、F1、F2 四个力作用。
(3)物体只受重力 G 和弹力 FN 的作用。
(4)力 FN、F1、F2 三个力的作用效果和 G、FN 两个力的作用效果相同。
- 图 3–21(a)中的小猩猩双臂悬挂时,双臂间的夹角与手臂上的拉力有何关系?
问题与思考解读
1.参考解答:用 1 cm 长的线段表示 5 N,作为标度。作力的图示,得到另一个分力约为 11 N,如图所示

命题意图:规范作图,根据平行四边形法则分解力。
主要素养与水平:科学推理(Ⅱ)。
2.参考解答:用尺和量角器规范作图。在同一平面内有两种可能性,在空间有无数种可能性
命题意图:理解力的分解的多样性。
主要素养与水平:科学推理(Ⅱ);科学论证(Ⅱ)。
3.参考解答:沿水平和竖直方向分解拉力。水平分力约为 10.4 N,竖直分力为 6 N
命题意图:为学习力的正交分解做准备。
主要素养与水平:科学推理(Ⅱ)。
4.参考解答:(1)错,F1 和 F2 是重力 G 的两个分力
(2)错,F1 和 F2 是重力 G 的两个分力
(3)正确
(4)正确
命题意图:体会合力与分力间等效替代的关系。
主要素养与水平:科学推理(Ⅰ);科学论证(Ⅱ)。
5.参考解答:把小猩猩作为研究对象,手臂上的拉力的合力不变。夹角越大,分力越大。
命题意图:了解简单的动态变化分析。
主要素养与水平:运动与相互作用(Ⅰ);模型建构(Ⅰ);科学推理(Ⅰ)。
发布时间:2021/7/12 下午9:13:24 阅读次数:7087
