第一章 第二节 位置的变化 位移

图 1–3 越野车和它在冰原上留下的车辙
随着经济和社会发展,汽车已成为生活中不可或缺的交通工。雪地上的车辙,显示了越野车的运动轨迹和经过的位置,形象生动地指向本节的内容主旨。如何确定运动物体的位置、描述位置的变化,是形成运动观念必须解决的基本问题。同时,通过节首图引出与描述位置变化有关的时间与时刻的概念。
本节编写思路
本节由生活经验、实例和自主活动提炼出时刻与时间间隔、位置、位移和路程的概念。
通过文字叙述和自主活动,从生活语言描述过渡到物理语言描述,引出用时间轴和坐标轴描述相关概念的方法,进而得到描述运动的位置一时间坐标(图像),总结出描述运动的三种基本方法:文字叙述、数学关系和图像。
在“自主活动”中掌习位移的测量方法,了解 DIS 实验和分体式位移传感器。
经历本节学习,学生将感受从具体到抽象、从经验到理性的科学思维方法。
由图 1–3 中越野车的车辙可以看出其位置在一段时间内发生了变化,车辙的终点反映了车在拍摄时所处的位置。物体位置随时间的变化与时间和时刻有关。时间和时刻既有联系又有区别。高铁 14 时发车, 17 时 30 分到达下一站。这里的 “ 14 时 ”和 “ 17 时 30 分 ” 就是高铁开始运动和结束运动的时刻,3 时 30 分是这两个时刻之间的时间间隔,即高铁的行驶时间。
图 1–4 时间轴
用数轴来表示时刻和时间,将其称为 “ 时间轴 ” 。如图 1–4 所示,时间轴上的点表示时刻,如 t1、t2;时间轴上的一段线段表示时间间隔,如 Δt = t2 − t1。如果将计时起点设为时间轴的原点,即 Δt1 = t1 − 0 = t1, Δt2 = t2 − 0 = t2。因此,通常用 t 来表示相对计时起点的时间间隔。
日常生活中通常所说的 “ 时间 ” 有时指的是时刻,有时指的是时间间隔。例如, “ 现在是北京时间 14 时 ” 说的是时刻, “ 我用 30 s 的时间通过手机订了一张电影票 ” 说的是时间间隔。
“时间”是日常生活用语,到底是指“某时刻”还是“某段时间间隔”通常需要通过前后文才能确定。在物理学中为了确切地对此加以描述,分别表述为“时刻”(用符号 t 表示)和“时间间隔”(用符号 Δt 表示)。在高中物理中,由于通常把时间起点取为 t = 0,因此有时符号 t 也表示时间间隔。
图 1–5 平面直角坐标系
为了描述物体的运动必须选定另一个物体作为参照,这个被选定的物体称为参考系(reference frame)。选择合适的参考系可以使问题的研究得到简化。如船舶在大海中航行时,我们通常以地球表面为参考系,在地球表面建立由经线和纬线构成的坐标系,用经度和纬度来确定其位置。若船舶的航行范围比较小,也可将该范围内的地球表面视为平面,在此平面内选定一个点作为坐标原点,建立相互垂直的 x 轴与 y 轴,在坐标轴上选取适当的长度单位表示空间尺度,用直角坐标系的坐标来确定船舶位置。图 1–5 中,在水平面内建立坐标系,船舶从 A (xA,yA)运动到 Aʹ (xAʹ,yAʹ),船舶的位置发生了变化。
由于我们处在三维空间之中,为了说明物体在空间的位置,需要确定参考系,并通过建立坐标系,用数学的语言加以精确描述。常用的坐标系有直角坐标系、平面极坐标系、球面坐标系等。
在高中物理中所涉及的主要是直角坐标系,如图1所示,抽象为质点的物体P在空间位置可由该质点在坐标系中的坐标(x,y,z)确定,也可由质点到原点的距离r和OP连线的方向余弦cosα = \(\frac{x}{r}\)、cosβ = \(\frac{y}{r}\),cosγ = \(\frac{z}{r}\)中的任意两个共同确定。无论用哪种方式,质点在三维空间的位置都需要三个独立的量描述。
从数学角度看,这是一种代数的方法,这样的描述显然不够简洁,因此在物理学中通过引入位置矢量来加以描述。位置矢量是一个由坐标原点指向质点所在位置的有向线段,用符号 r 表示,其大小 r(即矢量的模)表示质点与原点间的距离,其方向表示质点在空间的方位,由此,只需要一个矢量即可简洁地表示质点的空间位置。
如图 1–6 所示,从甲地出发去乙地的方式有很多,可以乘坐汽车、高铁、轮船、飞机等,无论选择何种交通工具,从甲地到乙地的位置变化都相同,但是通过的路径(或轨迹)并不相同。本章章导图中的光迹显示的就是车灯运动的轨迹。我们把物体在运动中通过的路径(或轨迹)的长度称为路程(path)。
在物理学中,物体位置的变化用物理量位移(displacement)来表示。我们用一条由起点指向终点的有向线段来表示位移。位移的大小就是从起点至终点的直线距离,方向由起点指向终点。在图 1–6 中,带箭头的红色有向线段表示从甲地到乙地的位移,线段的长度表示位移的大小,箭头的指向表示位移的方向。显然,根据物体的起点位置和位移,可以唯一确定其终点位置。图 1–6 所示的四种交通工具虽然经过的路程各不相同,但位移都相同;而且在任何情况下,路程均不小于位移的大小。
图 1–6 从甲地到乙地的路线图
在物理学中,把位移这类既有大小、又有方向的物理量称为矢量(vector),把温度、质量、路程这类只有大小、没有方向的物理量称为标量(scalar)。

图 1–7 某同学的行走路径
如图 1–7 所示,某同学从花园里的 A 点出发,沿着小路先向东走了 40 m 到达 B 点,再向北走了 30 m 到达终点 C。请在图上用有向线段表示从 A 到 B、从 B 到 C 的位移,并给出该同学在整个过程中的位移大小。
此处设置“自主活动”,在作图中初步建立矢量的概念,了解位移与路程的区别,知道整个过程的位移与前后两阶段位移之间并非代数和的关系,而是一种几何关系。为后续学习矢量的合成进行初步的渗透和铺垫。
参考答案如图 2 所示。
通过上述的自主活动发现, A 到 C 的位移大小为 A 、 C 间直线段的长度,并不等于 A 到 B 与 B 到 C 的路程之和。
为了定量描述物体沿直线运动的位移,我们以物体运动所在直线为坐标轴(x 轴),取直线上一点为坐标原点 O 并选择合适的标度和单位。这样,物体在任一时刻的位置均可以用 x 轴上的坐标来表示。
如图 1–8 所示,开始时质点位于位置 A, A 点坐标 xA = 2 m;然后该质点沿直线运动到位置 B, B 点坐标 xB = 5 m。质点的位移 ΔxAB 就是终点坐标与起点坐标之差,即
ΔxAB = xB − xA = 5 m − 2 m = 3 m
图 1–8 直线坐标轴
如果质点从位置 A 运动到位置 C, C 点坐标 xC = − 3 m,质点的位移 ΔxAC 可以表示为
ΔxAC = xC − xA=(− 3 m) − 2 m = − 5 m
此时质点位移的正负反映位移的方向;当位移为正时,质点位移沿 x 轴正方向;位移为负时,质点位移沿 x 轴负方向。
如果将质点出发的位置设为坐标原点,那么该质点沿 x 轴做直线运动时,运动到任意末位置 x1、x2 的位移 Δx1 = x1 − 0 = x1,Δx2 = x2 − 0 = x2。因此,质点沿 x 轴做直线运动时,通常用质点的位置 x 来表示质点相对坐标原点的位移。
在物体(质点)做直线运动情况下,用 x 轴上的坐标表示其位置。物体沿直线(x 轴)做一维运动时,只能向着 x 轴的正方向或负方向运动,此时可用代数量来表示位移矢量的大小和方向,用符号 Δx 表示,其定义是末位置坐标 x2 与初位置坐标 x1 之差,Δx > 0 表示位移方向沿 x 轴正方向,Δx < 0 表示位移方向沿 x 轴负方向。
图 1–9 所示是小球沿水平方向运动的频闪照片,并以 0 s 时小球的位置为坐标原点,沿小球运动方向建立 x 轴。通过对照片的分析,能够获得小球在运动过程中位置随时间变
化的数据。如 0.04 s 时,小球的位置 x1 = 0.02 m ;0.16 s 时,小球的位置 x2 = 0.08 m 。在这段时间内,小球在末时刻的位置 x2 与初时刻的位置 x1 之差就是小球在该段时间内的位移大小,即 Δx = x2 − x1 = 0.08 m − 0.02 m = 0.06 m。
小球的位置严格而言应是小球质心(即球心)位置(坐标)。

图 1–9 小球沿水平方向运动的频闪照片
为了直观地描述小球做直线运动的规律,我们以时间 t 为横轴、相对坐标原点的位移 x 为纵轴建立直角坐标系,然后根据图 1–9 中的数据,将小球在不同时刻相对于坐标原点的位移在坐标平面上描点后将其连成直线或平滑的曲线,从而得到小球位移随时间变化的图像,即小球运动的 x–t 图像。
物体运动时,其位置将随时间不断变化,因此对于运动的描述仅有位移信息是不够的,还必须给出时间信息。位移-时间图像用位移-时间坐标中的数据描述做直线运动物体的位置、时刻信息,即何时位于何处。并通过将数据点连接为函数图像,“形象”地表示物体运动过程,即相对原点的位移随时间的变化规律。在介绍描述运动的图像方法的同时,引导学生进一步认识运动总是发生在空间和时间之中,初步建立空间和时间相互联系的观念。
图1–10 小球运动的 x–t 图像
利用图 1–9 中的数据,在如图 1–10 所示的坐标平面中画出小球运动的 x–t 图像。该图像有什么特点?能直观反映出小球运动的哪些规律?
从图 1-9 读取小球的位置坐标或相对原点的位移 x 与对应时刻t的数据,在位移-时间坐标中描点,并用平滑曲线或直线连接数据点,得到小球的位移-时间(即 x-t)图像。由图像可直观得到小球的位移随时间线性增大的匀速直线运动特征,体会用图像描述直线运动的方法,感受运动的时空观。懂得物理规律常用文字叙述、数学关系和图像三种形式描述。
我们既可以用文字,也可以用图像来描述小球的运动规律。图像具有形象直观的特点。此外,物理量间的定量关系还可用数学关系式简洁、准确地表达。文字叙述、数学关系、图像是表述物理规律的三种常用方法。
物体位移的大小等于始、末位置间的直线距离。刻度尺是测量距离的传统工具。信息技术的发展给物理实验带来了不少便利。现在我们可以用位移传感器来测量距离。
分体式位移传感器由发射器和接收器两部分组成。使用时将两者正对,保持接收器位置不变,改变发射器的位置。通过连续测量发射器与接收器间的距离来确定各个时刻发射器的位置,得到发射器位移大小随时间变化的数据。
如图 1–11 所示,双手分别拿着分体式位移传感器的发射器和接收器,保持两者正对,仅移动发射器,测量发射器的位移随时间的变化。试一试,能否使发射器在一段时间内做匀速直线运动。
图 1–11 用传感器测量位移的大小
这个“自主活动”是第一个利用 DIS 进行测量的实验活动,其目的是:(1)学习和使用 DIS 进行测量,知道 DIS 界面显示实验数据的方式;(2)利用分体式位移传感器测量位移,初步了解速度的测量方法。
通过实验,应能分辨分体式位移传感器发射器、接收器的外部结构;学会传感器与数据采集器、计算机之间的连接及数据处理软件的使用;学会固定接收器,使接收器接收窗与发射器发射窗正对,以及完成测量后要关闭发射器上电源等操作要求;体验数据处理软件数字显示、图像两种界面的显示结果与发射器相对接收器实际位移的对应关系。在尝试使发射器做匀速直线运动的过程中,理解得到的位移-时间(即 x–t)图像的意义,并与发射器的运动情况相对应,感悟用图像描述运动的方法。
如图 1–12(a)所示,位移传感器由发射器和接收器组成,发射器内装有红外线和超声波发射器;接收器内装有红外线和超声波接收器。如图 1–12(b)所示,测量时,固定在被测运动物体上的发射器向接收器同时发射一个红外线脉冲和一个超声波脉冲,由于红外线传播时间可以忽略,接收器收到红外线脉冲时刻即可认为是脉冲的发射时刻,记为 t1,收到超声波脉冲时停止计时,记为 t2。计算机根据两者的时差
图1–12 位移传感器测距离的原理示意图
Δt2 = t2 − t1和空气中的声速,计算出发射器和接收器之间的距离。这就如雷雨时可以根据看到闪电和听到雷声的时差来计算雷电发生处到观察者的距离一样。不断发射脉冲就可以对运动物体进行跟踪定位。
除了位移的大小,其他物理量,如力、速度、温度、压强、电压、电流等,也都可以用数字化信息技术进行测量。采用这样的测量技术,并用计算机处理测量信息的实验称为数字化信息系统(Digital Information System,DIS)实验。
数字化信息系统主要包括数据采集、处理和显示三个部分。传感器采集物理信息,将其转化为电信号;电信号经处理转化为数字信息后可以呈现为数值、图像等形式。在数字化实验中,要根据所测的物理量选择不同的传感器,数据的处理和显示可由计算机实现。
- 选择合适的标度,把你们学校上午课表上的时刻标注在时间轴上(图 1–13)。在时间轴上标出从第三节课上课到第四节课下课间的时间间隔。
图 1–13
- 图 1–14 所示的圆形大花坛的环形道路半径为 r,某人从 A 点出发沿环形道路健身跑。当他的位移大小刚好等于环形道路的直径时,他经过的路程是多少?
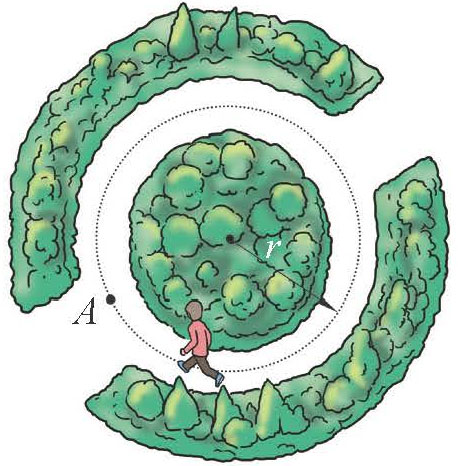
图 1–14
- 足球运动员进行折返跑训练。运动员先沿着 x 轴正向跑动,经 A 点到达 B 点后转身,沿 x 轴负向跑到 C 点。各点的位置如图 1–15 所示。试据此填写表 1–2。
图 1–15
表 1–2
|
A 点坐标 |
B 点坐标 |
C 点坐标 |
从 A 到 B 的位移 |
从 B 到 C 的位移 |
从 A 到 C 的位移 |
|---|---|---|---|---|---|
|
|
|
|
|
|
- 一跑步者在不同时刻的位置数据如表 1–3 所示,利用表中的数据在图 1–16 中作图。在 5.5 s 时,跑步者位于何处?如果跑步者继续按此规律运动,何时距离出发点 35 m?
表 1–3
图 1–16
|
时刻 t/s |
位置 x/m |
|---|---|
|
0.0 |
0.0 |
|
1.0 |
4.9 |
|
2.0 |
10.0 |
|
3.0 |
15.1 |
|
4.0 |
19.9 |
|
5.0 |
25.0 |
|
6.0 |
30.1 |
- 如图 1–17 所示为 A 、 B 两人运动的 x–t 图像。 A 保持匀速运动直达终点, B 晚出发一段时间。图中哪根图线表示 A 的运动? A 、 B 两人谁先到达终点?
图 1–17
1.参考解答:如图 3 所示
命题意图:在时间轴上表示时间和时刻,为后续运动图像的学习做准备,与学生的生活实际结合。
主要素养与水平:科学推理(Ⅰ)。
2.参考解答:此人沿着圆环跑动,因此当他的位移大小等于直径d时,他运动的路程有多种可能。为 πr(2n + 1)(n = 0,1,2,…)。
命题意图:体会位移和路程的区别。
主要素养与水平:运动与相互作用(Ⅰ);科学推理(Ⅱ)。
3.参考解答:8 m,21 m,15 m,13 m,−6 m,7 m
命题意图:用数学工具描述真实的运动,为了后续图像的学习做准备。
主要素养与水平:运动与相互作用(Ⅰ);解释(Ⅰ)。
4.参考解答:如图 4 所示,27 ~ 28 m,7 s 时
命题意图:从一维的坐标轴,到二维的坐标系,用图像表示运动的过程,为后续速度的学习、实验数据的处理做准备。
主要素养与水平:运动与相互作用(Ⅱ);解释(Ⅱ)。
5.参考解答:过原点的图线表示 A 的运动,不过原点的图线表示 B 的运动,A 先到终点。
命题意图:学会从用图像表示单一对象、单一过程的运动,到描述两个对象、多段过程的运动。
主要素养与水平:运动与相互作用(Ⅱ);科学推理(Ⅱ)。
发布时间:2021/6/28 下午10:58:05 阅读次数:7221
