第 2 章 第 2 节 位移变化规律

对于匀变速直线运动，我们已经知道物体运动的速度随时间变化的规律，那么物体运动的位移随时间变化有着怎样的规律呢？本节我们将学习匀变速直线运动的位移-时间关系和位移-速度关系。

1．匀变速直线运动的位移-时间关系

在匀速直线运动中，物体运动的速度不变，因此位移 s ＝ vt，这在数值上恰好等于 v-t 图像中着色部分的面积[图2-7（a）]。

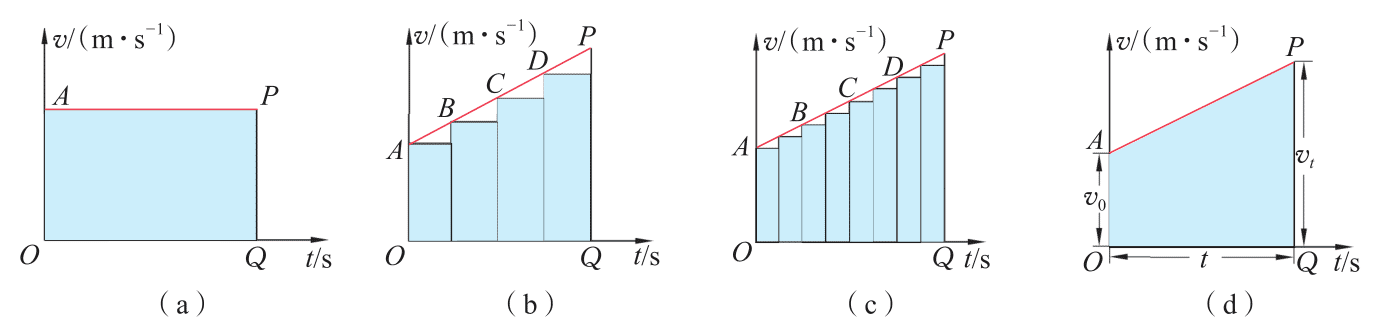
在匀变速直线运动中，由于运动速度不断变化，无法采用前面的方法直接计算出位移。不过，我们可设想将匀变速直线运动v-t图像中的时间分为许多小的时段，在每个时段中，认为物体近似以某一速度做匀速直线运动，每个时段所对应的位移在数值上等于该时段对应的矩形面积[图2-7（b）]。时段划分越细，设想的运动就越接近真实运动，矩形面积之和就越接近梯形OAPQ的面积[图2-7（c）]。当所取的时段足够小时，设想的运动便可等同于真实运动，矩形面积之和便等于梯形面积[图2-7（d）]。该梯形面积在数值上便等于匀变速直线运动的位移大小，即

\[s = \frac{1}{2}({v_0} + {v_t})t\]

将 v_t＝v₀＋at 代入上式，有

\[s = {v_0}t + \frac{1}{2}a{t^2}\]

这个数学关系式通常称为匀变速直线运动的位移公式，它描述了匀变速直线运动的位移随时间变化的规律，即位移-时间（s-t）关系。根据这个公式，知道了初速度和加速度，就能确定在不同时间内物体运动的位移。

方法点拨

推导中用到了微积分的思想，即无限分割微元求和、逐渐逼近真实状况的思想。在物理学研究中常常用到这种思想。

素养提升

能在特定情境中运用匀变速直线运动模型解决问题；能用科学研究中的极限方法分析物理间题，通过推理，获得结论。

——科学思维

同样，我们还可用图像直观描述匀变速直线运动的位移与时间的关系。

仍以图2-1所示的汽车运动为例。选汽车行驶的时间t为横坐标，汽车相对于其起始位置的位移s为纵坐标，分别在坐标纸上描出相应的点，再将各点用平滑曲线连接起来，便可得到位移随时间变化的s-t图像（图2-8）。

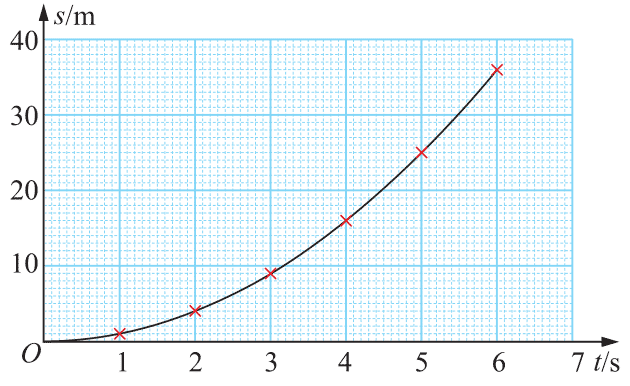
从 s-t 图像中我们可直观看出物体运动过程中位移随时间的变化情况，并可求出不同时间内物体运动的位移。

2．匀变速直线运动的位移-速度关系

对于一个以加速度a做匀变速直线运动的物体，有时仅知道物体运动的初速度 v₀ 和末速度 v_t，怎么确定物体的位移呢？

我们可把公式 v_t ＝ v₀＋at 和 s ＝ v₀t＋\(\frac{1}{2}\)at² 联立，消去时间t，得到一个新的公式

\[v_t^2 - v_0^2 = 2as\]

这便是匀变速直线运动的位移-速度（s-v）关系式。根据这个公式，在没有时间信息时，我们也可用位移与速度的关系分析物体运动的相关情况。

例题

汽车从开始制动到停止所行驶的距离，是衡量汽车制动性能的参数之一。某型号的汽车以 100 km/h 的速度在柏油路面上行驶，急刹车后做匀减速直线运动。若匀减速时的加速度大小为 5 m/s²，开始制动后 2 s 内汽车行驶的距离是多少？从开始制动到完全停止，汽车行驶的距离是多少？

分析

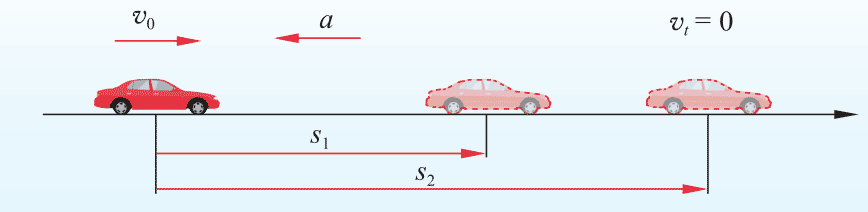
汽车刹车后做匀减速直线运动，运动过程如图 2-9 所示。在第一问中，已知初速度、加速度和时间的信息求位移，可用位移-时间关系式；在第二问中，通过初速度、加速度和末速度的信息求位移，可用位移-速度关系式。

解

选定初速度方向为正方向，由题意知 v₀ ＝ 100 km/h ＝ 27.8 m/s，a ＝－5 m/s²，v_t ＝ 0，t ＝ 2 s。

根据速度公式 v_t ＝ v₀ ＋ at，可知汽车刹车时间

\[{t_0} = \frac{{{v_t} - {v_0}}}{a} = \frac{{0 - 27.8{\rm{m/s}}}}{{ - 5{\rm{m/}}{{\rm{s}}^{\rm{2}}}}} = 5.56{\rm{s}}\]

因为 t＜t₀，所以汽车在刹车后 2 s 内一直运动。根据位移公式，可得开始制动后 2 s 内汽车的位移

\[\begin{array}{l}{s_1} = {v_0}t + \frac{1}{2}a{t^2}\\ = 27.8{\rm{m/s}} \times 2{\rm{s}} + \frac{1}{2} \times ( - 5{\rm{m/}}{{\rm{s}}^{\rm{2}}}) \times {(2{\rm{s}})^2}\\ = 45.6{\rm{m}}\end{array}\]

根据公式 v_t²－v₀²＝2as，可得汽车从开始制动到完全停止的位移

\[\begin{array}{l}{s_2} = \frac{{v_t^2 - v_0^2}}{{2a}}\\ = \frac{{0 - {{(27.8{\rm{m/s}})}^2}}}{{2 \times ( - 5{\rm{m/}}{{\rm{s}}^{\rm{2}}})}}\\ = 77.3{\rm{m}}\end{array}\]

所以，开始制动后 2 s 内汽车行驶的距离为 45.6 m；从开始制动到完全停止，汽车行驶的距离为 77.3 m。

策略提炼

关于匀变速直线运动的问题，通常涉及v₀、v_t、a、t和s这五个物理量，以及v-t、s-t和s-v关系式。在选用关系式时，首先看问题情境中有哪些已知量与未知量，再看这些量出现在哪个关系式中，最后确定所用的关系式。这是解决该类问题比较便捷的方法。

运用公式时，要注意速度、加速度与位移的方向，由此确定代入数据的正负号。

讨论

一般以速度 100 km/h 行驶的汽车，从开始制动到完全停止的距离为几十米。本题的计算结果在合理范围内。

由于汽车从刹车到停止仍需行驶一段距离，同向行驶的汽车之间需保持一定的安全距离。你认为以 100 km/h 行驶的汽车需与前车保持多大的安全距离？把你的看法与查阅的相关数据进行比较。此外，在其他条件不变的情况下，汽车从开始制动到完全停止所行驶的距离与刹车时速度的平方成正比。你能证明吗？当汽车行驶速度增大时，该距离将显著增大。因此，汽车超速行驶极易引发交通事故。

迁移

我国道路交通安全法规定，机动车因故障在高速公路临时停车时，需在故障车来车方向 150 m 以外设置警告标志。某司机驾驶汽车以 120 km/h 的速度在高速公路上匀速行驶，发现前方警告标志时刹车使汽车减速至停止。该司机从发现警告标志到汽车开始制动的反应时间为0.6 s，制动时的加速度大小为 5 m/s²。假设制动后，汽车做匀减速直线运动，那么从司机发现警告标志到汽车停下，行驶的距离是多少？请解释上述交通法规的必要性。

素养提升

能理解位移、速度和加速度的内涵，能用公式、图像等方法描述匀变速直线运动；自用匀变速直线运动的规律解释生活中的一些现象。具有与直线运动相关的初步的运动观念。

——物理观念

节练习

1．一辆电动车以 4 m/s 的速度沿直线匀速行驶，然后以 1 m/s² 的加速度匀加速行驶。求电动车匀加速行驶 10 m 时的速度。

【解答】6 m/s

2．若某汽车以 18 m/s 的速度行驶，刹车后做匀减速直线运动，加速度大小为 4 m/s²，求刹车后 5 s 内汽车前进的距离。

【解答】40.5 m

3．如图所示，在某一段平直的铁路上，一列以 144 km/h 的速度行驶的动车开始匀减速行驶，经过 2 min，动车恰好停在车站；在车站停留 4 min，动车匀加速驶离车站，离开车站 2 km 时恢复到原来的速度 144 km/h，求：

（1）动车减速时的加速度大小；

（2）动车从开始减速到恢复到原速度这段时间内的平均速度大小。

【解答】（1）a ＝ －0.33 m/s²

（2）9.6 m/s

4．某型号的汽车在以 72 km/h 的速率行驶时，可以在 54 m 的距离内停下来；在以 36 km/h 的速率行驶时，可以在 17 m 的距离内停下来。假设两次刹车中，驾驶员的反应时间和刹车的加速度都相同，求驾驶员的反应时间和刹车时加速度的大小。

【解答】t ＝ 0.7 s，a ＝ 5 m/s²

5．试证明：做匀变速直线运动的物体在一段时间内的平均速度等于这段时间中间时刻的瞬时速度。

*6．做匀变速直线运动的物体，设在各个连续相等的时间t内的位移分别是 s₁，s₂，s₃，…，s_n。如果物体的加速度是 a，试证明：

（1）s₂－s₁＝s₃－s₂＝…＝s_n－s_n－1＝at²；

（2）s₄－s₁＝s₅－s₂＝s₆－s₃＝3at²。

参考解答：

证明：根据公式 s = v₀t + \(\frac{1}{2}\)at²，得

s₁ = v₀t + \(\frac{1}{2}\)at²

s₂ = v₀×(2t) + \(\frac{1}{2}\)a(2t)² – s₁ = v₀t + \(\frac{3}{2}\)at²

……

s_n = s_n − s_n－1 = v₀×(nt) + \(\frac{1}{2}\)a(nt)² – { v₀×[(n – 1)t) + \(\frac{1}{2}\)a[(n – 1)t]²}

= v₀t + \(\frac{2n  – 1}{2}\)at²

s_n − s_n－1 = at²

（2）s₄ − s₁ = (s₄ – s₃) + (s₃ – s₂) + (s₂ – s₁) = 3at²

s₅ – s₂ = (s₅ – s₄) + (s₄ – s₃) + (s₃ – s₂) = 3at²

s₆ – s₃ = (s₆ – s₅) + (s₅ – s₄) + (s₄ – s₃) = 3at²

所以，s₄ − s₁ = s₅ − s₂ = s₆ − s₃ = 3at²

发布时间：2021/6/4 下午10:27:22  阅读次数：2872