第 2 章 第 1 节 速度变化规律

在物理学中，将物体速度发生变化的运动称为变速运动。做变速运动的物体，其速度变化是否存在规律？一般来说，做变速运动的物体速度变化情况非常复杂。我们先从最简单的变速运动开始，讨论匀变速直线运动的速度变化规律。

1．匀变速直线运动的特点

什么是匀变速直线运动？

我们以一辆从静止开始沿直线运动的汽车为例（图2-1）。若在某段路程中，每隔1 s测一个速度值，所得数据见表2-1。

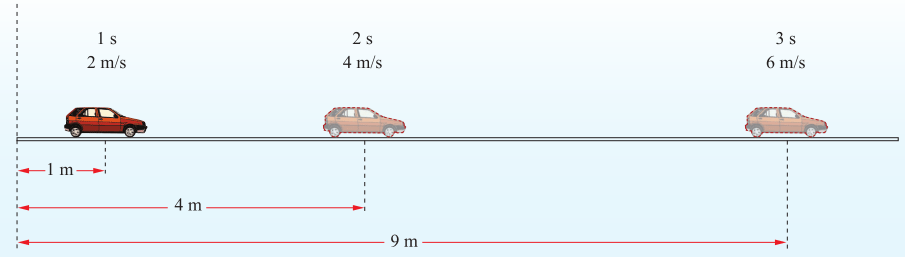
表2-1 汽车沿直线运动时速度随时间变化的数据

将表2-1中两个时刻对应的速度值代入加速度定义式，可得该车加速行驶时的加速度值。例如，分别将2 s和3 s这两个时刻所对应的速度值代入加速度定义式，得

\[a = \frac{{{v_t} - {v_0}}}{t} = \frac{{6{\rm{m/s}} - 4{\rm{m/s}}}}{{1{\rm{s}}}} = 2{\rm{m/}}{{\rm{s}}^{\rm{2}}}\]

若继续将汽车任意两个时刻所对应的速度值代入加速度定义式，皆可得到相同的加速度值，则可认为该车在行驶时，加速度保持不变。

物理学中，将物体加速度保持不变的直线运动称为匀变速直线运动（rectilinear motion with constant acceleration）。

匀变速直线运动是一种简单且特殊的变速直线运动，是一种物理模型。物体在做匀变速直线运动过程中，加速度的大小和方向都不改变。当加速度与速度同向时，物体做匀加速直线运动；当加速度与速度反向时，物体做匀减速直线运动。为了便于研究，人们通常将某些物体的运动（或其中的一段运动）近似视为匀变速直线运动。

2．匀变速直线运动的速度-时间关系

当物体做直线运动时，根据加速度的定义式可得

\[{v_t} = {v_0} + at\]

这个公式描述了做匀变速直线运动的物体速度随时间变化的规律，通常称为匀变速直线运动的速度公式。公式中，v_t为物体在时刻t的速度，v₀为初速度。通常设v₀的方向为正方向，当a＞0时，a与v₀的方向相同，物体做匀加速直线运动；当a＜0时，a与v₀的方向相反，物体做匀减速直线运动。若v₀＝0，速度公式变为v_t＝at，v_t与a总是同向，物体做匀加速直线运动。

例题

一辆汽车以54 km/h的速度在平直公路上行驶，司机看见前方路口红灯亮时立即刹车。若汽车刹车时的加速度大小为3 m/s²，则刹车后4 s末的速度是多少？

分析

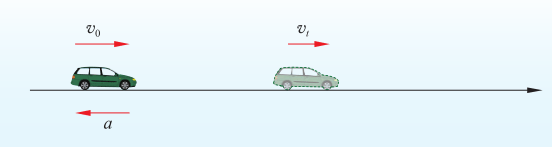
刹车后，汽车的运动可视为匀减速直线运动，加速度方向与速度方向相反（图2-2）。可将已知量代入速度公式求解。

解

选定初速度方向为正方向，由题意可知，v₀＝54 km/h＝15 m/s，t＝4 s，a＝－3 m/s²。

根据匀变速直线运动的速度公式得

\(\begin{array}{l}{v_t} = {v_0} + at\\ = 15{\rm{m/s}} + ( - 3{\rm{m/}}{{\rm{s}}^{\rm{2}}}) \times 4{\rm{s}}\\ = 3{\rm{m/s}}\end{array}\)

所以，汽车刹车后4 s末的速度是3 m/s。

讨论

v_t＞0说明汽车未停下，计算结果合理。

策略提炼

求解运动问题，通常是先明确运动情境，并画出运动示意图；再根据已知量和未知量，选择相应运动规律列方程求解；最后需要对求解结果的合理性进行判断。

运用公式前，需要选定正方向，并由此确定已知量中矢量的正负，再代入公式计算。

迁移

求解物理问题时，不能盲目将数据代入公式，应关注问题的物理情境。上题中，若求汽车刹车后6 s末的速度，结果又如何？请算一算，并说明理由。

我们不仅可用公式描述做匀变速直线运动的物体速度随时间变化的规律，还可用图像直观地描述这一变化规律。

仍以图2-1所示的汽车运动为例，选汽车行驶的时间t为横坐标，汽车的速度v为纵坐标，在坐标纸上描出相应的点，将各点用平滑曲线连接，便得到如图2-3所示的图像。该图像描述了汽车匀加速直线行驶时速度与时间的关系，通常称为速度-时间图像（v-t图像）。匀变速直线运动的v-t图像是一条倾斜的直线。

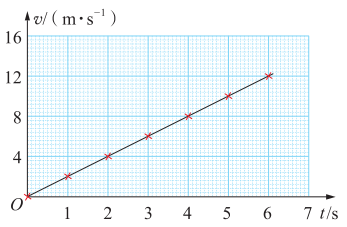
根据v-t图像，我们可直观了解物体运动速度随时间变化的规律，可较准确地判断某时刻物体的运动速度或物体达到某速度所需要的时间，还可求出物体的加速度。

由图2-3可知汽车匀加速直线行驶时不同时刻对应的速度，还可求出汽车的加速度：a＝\(\frac{{{v_t} - {v_0}}}{t}\)＝\(\frac{{12{\rm{m/s}}}}{{6{\rm{s}}}}\)＝2 m/s²。

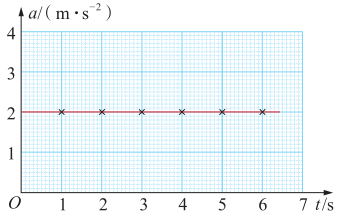
如果选时间t为横坐标、加速度a为纵坐标，可得到加速度随时间变化的图像，通常称为a-t图像。做匀加速直线运动的汽车，在任意时刻加速度都不变，其a-t图像为平行于时间轴的直线（图2-4）。

方法点拨

物理公式能简洁地描述自然规律，物理图像则能直观地描述自然规律。利用公式或图像，由题目中的已知量可求出未知量。例如，利用匀变速直线运动的速度公式或v-t图像，可求出物体的速度、运动时间和加速度等。

用公式或图像描述物理规律通常有一定的适用范围，只能在合理的条件下外推。例如，讨论汽车以加速度a＝2 m/s²运动时，若将时间t推延至2 h，即7 200 s，这在数学上没有问题，但是在物理上，得出的结果则是不合理的，即汽车速度达到了14 400 m/s。这显然是不符合实际情况的。

物理聊吧

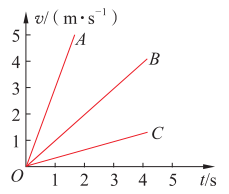
（1）图2-5给出了A、B、C三辆车的v-t图像，在不计算的情况下，你能推断出这三辆车加速度的大小排序吗？分别估算这三辆车的加速度，看看结果与你的判断是否一致，并与同学交换看法。

（2）图2-6（a）和（b）分别表示的是什么运动？初速度是否为0？是加速还是减速？请说说你判断的理由。

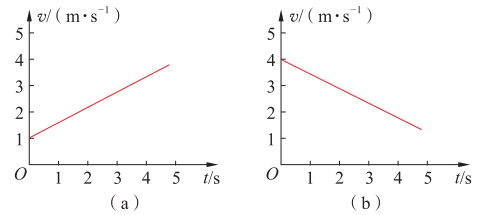
节练习

1．某轿车在紧急刹车时加速度大小为6 m/s²。如果必须在5 s内停下来，该轿车的行驶速度最大不能超过多少？

【解答】30 m/s

2．在交通信号灯绿灯亮起时，一辆汽车由静止出发，以2.5 m/s²的加速度做匀加速运动。要使它的速度达到12 m/s，需要多长时间？

【解答】4.8 s

3．一架以145 m/s的速度飞行的超音速飞机，以23.1 m/s²的加速度沿直线匀加速飞行20 s后，速度达到多大？此时飞机速度是声音速度的多少倍？（取声音在空气中的传播速度为331 m/s）

【解答】607 m/s，1.83倍

4．一辆摩托车沿直线运动时，速度随时间变化的数据见下表。摩托车在0～15 s和15～30 s两段时间内近似视为做匀变速直线运动。

（1）求摩托车在第一个10 s内的加速度。

（2）请根据表中数据画出摩托车运动的v-t图像。

（3）根据画出的v-t图像求出第一个10 s内的加速度，并与（1）中的计算结果进行比较。

（4）求摩托车在15～30 s内的加速度。

【解答】（1）a＝2 m/s²

（2）如图所示

（3）a＝2 m/s²，所得结果与（1）中结果相同。

（4）a＝－2 m/s²

5．请对比观察如图所示的两个不同物体运动的s-t图像和v-t图像，分析并指出图（a）（b）中的OA、AB、BC、CD各段图线分别表示物体做怎样的运动。

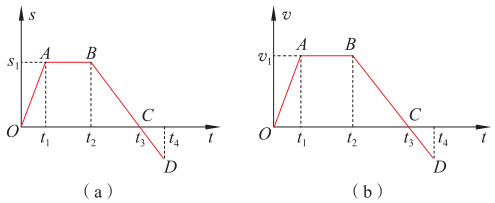
【解答】

6．某物体在水平方向做直线运动的v-t图像如图所示。请根据图像画出物体运动过程的示意图，并求出各运动阶段的加速度。

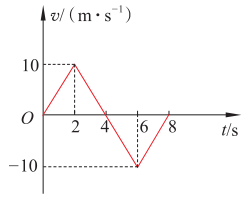
【解答】（1）物体运动过程的示意图，如图所示。

（2）由a＝\(\frac{{{v_t} - {v_0}}}{t}\)，可计算出物体各运动阶段的加速度如下表。

发布时间：2021/5/25 下午10:24:19  阅读次数：3433