第3章 第3节 离心现象

如果你仔细观察高速公路转弯处的路面及铁路转弯处的轨道，会发现这些地方都是外高内低，这样的设计有什么道理？本节将通过实例分析做圆周运动的物体所需的向心力。

1．车辆转弯时所需的向心力

汽车在水平路面上转弯时（图 3-18），有向外侧滑的趋势，地面会对汽车产生指向内侧的静摩擦力。这时在指向圆心的方向上存在静摩擦力 f 的作用，该力提供了汽车转弯所需的向心力。根据向心力公式 f = m\(\frac{{{v^2}}}{r}\)，如果弯道半径一定，汽车速度超过一定限度时，汽车就会向外侧滑。

为了给汽车、火车提供转弯时所需的向心力，高速公路、铁路的弯道通常都设计成外高内低。这样，汽车、火车转弯时，可依靠重力与支持力的合力获得向心力。例如，按限定速度转弯的火车，受到重力和支持力的作用，此时重力和支持力的合力 F 不为 0，而是指向弯道的圆心，合力 F 就提供了火车转弯时做圆周运动的向心力。

如图 3-19 所示，假设弯道的倾角为θ，则F = mgtanθ，根据向心力公式 mgtanθ = m\(\frac{{{v^2}}}{r}\)，可得

\[v = \sqrt {gr\tan \theta } \]

从上式可以看出，通过弯道时限定速度的大小取决于弯道半径和倾角。

火车车轮上有突出的轮缘，以保证车轮能行驶在铁轨上。对于半径、倾角都确定的某个弯道而言，如果车速合适，重力与支持力的合力恰好提供火车转弯时所需的向心力。但如果车速过快，这个合力不足以提供所需的向心力，外侧车轮轮缘就会与外轨发生挤压，以补充缺少的向心力，这样会损坏外轨，甚至造成脱轨。因此，火车转弯时都要限速。飞行中的飞机要改变飞行方向时，飞机的机身也要倾斜（图 3-20）。与车辆不同的是，飞机转弯时所需的向心力由重力和空气对它的作用力的合力提供。

2．竖直平面内的圆周运动分析

汽车在经过凸形路面和凹形路面时都不宜高速行驶，这是为什么呢？下面我们通过实验来探究其中的道理。

迷你实验室

凹凸桥

（1）用两根铁丝弯成如图 3-21 所示的凹凸桥。首先，把一个小球放在凹桥底部A处，调节两轨间的距离，使球刚好不掉下去，但稍加一点儿压力，球就会撑开两轨下落。然后，让球从斜轨滚下。当球经过凹桥底部 A 处时，你观察到了什么？

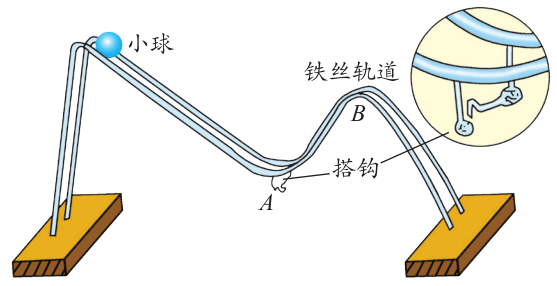
（2）把凹桥下面的搭钩扣上，并调整凸桥顶端 B 处两轨间的距离，使小球在 B 处放置时，刚好能在此处撑开两轨下落。然后，让小球从斜轨滚下。当球经过凸桥顶端 B 处时，你又观察到了什么？

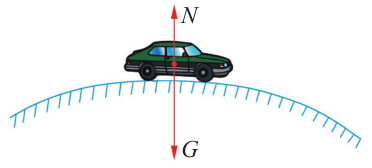
通过实验你会发现，小球运动到凹桥底部时从两轨间掉了下去，这说明运动的小球对凹桥底部的压力大于静止时的压力；小球运动到凸桥顶端时没有落下，而是从桥面掠过，这说明运动的小球对凸桥顶端的压力小于静止时的压力。类似地，如图 3-22 所示，汽车驶过凸形路面的顶端时，所受的重力和支持力同在竖直方向，此时汽车行驶所需的向心力就由这两个力的合力提供。那么，由向心力公式 G－N = m\(\frac{{{v^2}}}{r}\)可知，N ＜ G。根据牛顿第三定律，汽车行驶到凸形路面顶端时对路面的压力小于汽车受到的重力，此时汽车处于失重状态而不易被控制，并且速度越大越易失控。因此，汽车在经过凸形路面时不宜高速行驶。

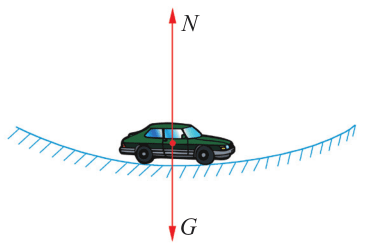
同样的道理，如图 3-23 所示，汽车行驶到凹形路面底部时，汽车对路面的压力将大于重力，容易出现超重现象而引发爆胎。因此，汽车在经过凹形路面时也不宜高速行驶。

在游乐场里，惊险又有趣的项目之一就是坐过山车。如图 3-24 所示的过山车轨道是由很高的滑轨和环形轨道构成的。过山车高速驶过环形轨道顶端时，人们不会有从轨道上掉下来的感觉。我们继续学习下面的内容，就能明白其中的道理。

迷你实验室

实验室的“过山车”

用两根铁丝弯成如图 3-25 所示的形状。将小球从斜轨的某一高度释放，然后逐步改变小球的释放点，看小球能否越过环形轨道的顶端并继续沿轨道运行而不掉落。

如图 3-26 所示，当小球沿圆环内侧轨道经过最高点时，向心力 F = mg + N ，根据向心力公式可得 mg + N = m\(\frac{{{v^2}}}{r}\)。当 N = 0 时，mg = m\(\frac{{{v^2}}}{r}\)，小球恰好能通过最高点，此时，小球的速度 v = \(\sqrt {gr} \)，所需的向心力完全由重力提供。可以看出，小球能通过最高点的条件是在最高点的速度大小v ≥\(\sqrt {gr} \) 。

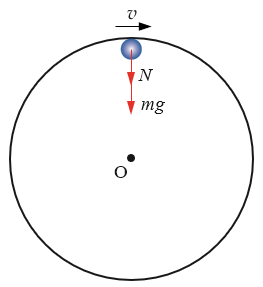
现在，你知道为什么过山车到达轨道顶端时，人们不会有掉下来的感觉了吧？

3．生活中的离心运动

在生活中时常会出现这样一些现象：做圆周运动的物体失去向心力时会沿着圆周的切线方向飞出。例如，用绳子系着小球用力旋转，使小球做圆周运动，一旦松手或者绳子断裂，小球就会沿着它所在处圆弧的切线方向飞出（图 3-27）。

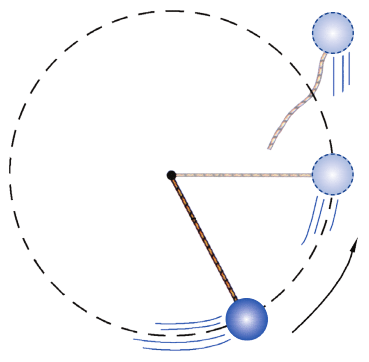
为什么会出现上述情况？我们知道，做圆周运动的物体的线速度方向就沿圆周的切线方向。物体之所以没有飞出去，是因为它受到的合外力提供了它所需要的向心力。一旦松手或者绳子断裂，向心力立刻消失，物体会因惯性沿着圆周的切线方向飞出。为了防止做圆周运动的物体脱离圆周而造成事故，人们会采取保护措施。例如，投掷链球的场地除了链球出口处，周围要用铁丝网围住，防止因链条断裂或运动员意外脱手而引发事故。

当物体受到的合外力不足以提供物体做圆周运动所需的向心力时，物体又会怎样运动？ 让我们通过一个小实验来探究。

迷你实验室

人造“墨水旋风”

用光滑的白色厚纸做成圆板，将铁钉插在圆板中心，做成陀螺。然后，在圆板上滴几滴墨水。在墨水未干之前，轻轻旋转陀螺。当陀螺停止旋转时，墨水痕迹会变成旋风状（图 3-28）。

怎样解释上面的实验现象呢？我们知道，圆板与墨水之间存在着相互作用力，这种力使得墨水在白纸上不会轻易流动。随着圆板旋转加快，圆板与墨水之间的相互作用力不足以提供墨水做圆周运动所需要的向心力，墨水就会离圆心越来越远。

通过上面的实验与分析可以知道，做圆周运动的物体，在受到的合外力突然消失或者不足以提供做圆周运动所需要的向心力的情况下，将远离圆心运动，我们把这种运动称为离心运动。这种现象称为离心现象。

在科研和生产中常用到离心机械。例如，医院和科研机构常用离心分离器加快液体中密度不同成分的分离，铸造工业采用离心铸造工艺提高铸件质量，纺织工业用离心干燥器甩掉附着在织物上的水分……

洗衣机的脱水筒也是利用离心运动原理设计的。当脱水筒快速转动时，脱水筒内水与衣物之间的附着力如果小于水做圆周运动所需要的向心力，水就会与衣物分离，被甩出脱水筒。

物理聊吧

（1）游乐场的旋转盘上，开始时有的人离转轴近一些，有的人离转轴远一些（图 3-29）。当旋转盘加速时，哪些人更容易发生滑动？为什么？

（2）握住体温计的顶部用力甩，就能把水银甩回玻璃泡内。如何解释这个现象？医院每天要用很多支温度计，如果一支支地甩，是很费时间的。你能想到简便方法吗？请上网查询，或者实地调研，然后与同学分享你调研的结果。

有些离心运动会对身体造成伤害。例如，飞机翻飞旋转时，离心运动会造成飞行员瞬间大脑缺血、四肢沉重，这种现象即为过荷。严重时，飞行员会暂时失明甚至昏厥。飞行员可以通过加强训练来提高抗荷能力。利用离心机可以研究过荷对人体的影响，测试和训练人体的抗荷能力。通过训练，可以减轻离心运动对人体的伤害。

有些离心运动会带来危险。如汽车在水平路面转弯时所需的向心力是由车轮与地面间的静摩擦力提供的，如果转弯所需的向心力大于最大静摩擦力，汽车将做离心运动，容易造成事故。为了防止事故的发生，汽车转弯时应放慢行车速度。

素养提升

会用线速度、角速度、周期描述圆周运动，知道向心加速度的内涵，能分析匀速圆周运动的向心力；能用向心力及向心加速度等解释生产生活中的离心现象及其产生的原因。具有与匀速圆周运动相关的运动与相互作用的观念。

——物理观念

节练习

1．如图所示，用绳子拴着小球转动。如果使小球越转越快，必须用越来越大的力拉住绳子，同时绳子也越来越接近水平。分析一下，绳子可能被拉至水平吗？

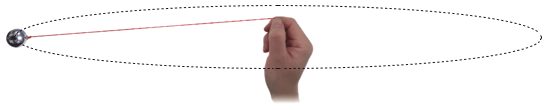
【解答】绳子不可能被拉至水平。因为小球受到的重力是竖直向下的，需要未水平的绳子提供竖直向上的分力来平衡小球的重力。

2．铁路的弯道通常都设计成外高内低。若某转弯处的限定速度为 v，当火车以该限定速度通过时，请分析此时火车所需向心力的来源。若火车的实际速度低于限定速度，对铁轨有何影响？

【解答】火车以限定速度v通过这个转弯处时，受到的重力及轨道面的支持力这两个力的合力提供了转弯时的向心力，铁轨对车轮没有侧压力。当火车速度小于v时，转弯时所需要的向心力也随之减小，火车受到的重力及轨道面的支持力这两个力的合力大于所需提供的向心力，火车将挤压内轨。

3．如图所示，质量相等的甲、乙两物体放在旋转的圆台上，甲物体到转轴的距离是乙物体到转轴距离的两倍，甲、乙与圆台间的最大静摩擦力相等。当圆台旋转时，甲、乙均未滑动。请分析当圆台的转速逐渐增大时哪个物体先滑动，并说明理由。

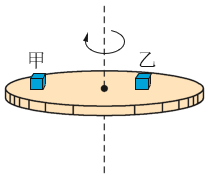
【解答】甲先滑动。

甲、乙两物体角速度相等，根据F_n＝ma_n＝mrω²，又因为μmg＝mrω²，所以ω＝\(\sqrt {\frac{{\mu g}}{r}} \)。因为甲的圆周运动半径大，所以甲的临界角速度小，当圆台转速增加时，甲先滑动。

4．长为l的轻绳，其一端固定于O点，另一端连有质量为m的小球，该小球绕 O 点在竖直平面内做圆周运动，g 为重力加速度。求：

（1）小球刚好到达最高点时的速度；

（2）小球到达最高点速度为 2\(\sqrt {gl} \)时轻绳受到的拉力。

【解答】（1）v＝\(\sqrt {gl} \)

（2）T＝3mg，竖直向上。

5．摩托车通过一座拱形桥顶部时速度为 10 m/s，此时车对桥面的压力只有重力的\(\frac{3}{4}\)。如果摩托车通过该桥顶部对桥面的压力只有重力的\(\frac{1}{4}\)，则车的速度为多大？

【解答】17.3 m/s

*6．一把打开的雨伞半径为 r，伞边缘距水平地面的距离为 h。当该雨伞绕伞柄以角速度 ω 水平旋转时，雨点自边缘甩出下落，在地面上形成一个大圆圈。已知重力加速度为 g。试求这个大圆圈的半径。

【解答】R＝r\(\sqrt {1 + \frac{{2h{\omega ^2}}}{g}} \)

发布时间：2021/2/26 下午10:23:34  阅读次数：5571