第五章 3 核力与结合能
问题？
原子核是由中子和质子构成的。在原子核那样狭小的空间里，是什么力量把带正电的质子紧紧地束缚在一起而不飞散开呢？
核力与四种基本相互作用
现代物理学认为，自然界存在着四种基本相互作用，即引力相互作用、电磁相互作用、强相互作用和弱相互作用。自然界中的各种力，都可以归结为这四种相互作用。
17 世纪下半叶，人们发现了万有引力。正是万有引力把行星和恒星聚在一起（图 5.3–1），组成太阳系、银河系和其他星系。引力是自然界的一种基本相互作用，地面物体所受的重力只是引力在地球表面附近的一种表现。
19 世纪后，人们逐渐地认识到，电荷间的相互作用、磁体间的相互作用，从本质上说是同一种相互作用的不同表现，这种相互作用称为电磁相互作用（electromagnetic interaction）或电磁力。它也是自然界的一种基本相互作用。我们知道，宏观物体中包含了大量带负电的电子和带正电的原子核。宏观物体之间的压力、拉力、弹力、支持力等等，都起源于这些电荷之间的电磁相互作用。
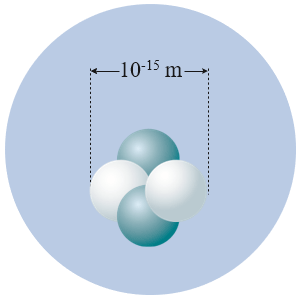
20 世纪，物理学家发现原子核是由若干带正电荷的质子和不带电的中子组成的。然而，带正电的质子之间存在相互排斥的电磁力，这种斥力比它们之间的万有引力大得多，似乎质子与质子结合在一起是不可能的。物理学家们发现，原子核中的核子之间存在一种很强的相互作用，即存在一种核力，它使得核子紧密地结合在一起，形成稳定的原子核（图 5.3–2）。这种作用称为强相互作用（strong interaction）。与万有引力和电磁力不同，距离增大时，强相互作用急剧减小，它的作用范围只有约 10−15 m，即原子核的大小，超过这个界限，这种相互作用实际上已经不存在了，它是短程力。这样，万有引力、电磁力和强相互作用分别在不同的尺度上发挥了作用。
19 世纪末 20 世纪初，物理学家发现了放射现象。后来发现，在某些放射现象中起作用的还有另一种基本相互作用，称为弱相互作用（weak interaction）。[1]弱相互作用是引起原子核β衰变的原因，即引起中子—质子转变的原因。弱相互作用也是短程力，其力程比强相互作用更短，只有10−18 m。
结合能
我们考虑下面的问题。相距很远的两个物体，由于万有引力而相互接近，运动速度越来越大，引力势能转化为动能。最后撞在一起，一部分动能变成热并散失掉了。两个物体为了结合而付出了代价——失去了一些能量，如果要把它们分开，还要重新赋予它们能量。
类似地，要使基态氢原子电离，也就是要从氢原子中把电子剥离，需要通过碰撞、施加电场、让氢原子吸收光子等途径使它得到相应的能量。
思考与讨论
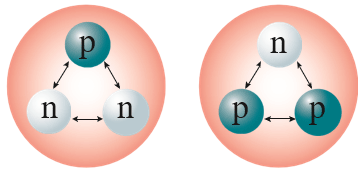
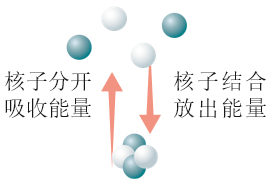
如图 5.3–3，氦原子核是由两个质子和两个中子凭借核力结合在一起的，要把它们分开，需要吸收能量。反过来，4 个核子结合成氦原子核要放出能量。那么，把核子分开需要的能量与核子结合放出的能量有什么关系？
原子核是核子凭借核力结合在一起构成的，要把它们分开，也需要能量，这就是原子核的结合能（binding energy）。这个能量也是核子结合成原子核而释放的能量。
自然，组成原子核的核子越多，它的结合能越大。原子核的结合能与核子数之比，叫作比结合能（specific binding energy），也叫作平均结合能。比结合能越大，原子核中核子结合得越牢固，原子核越稳定。
质量亏损
原子核的结合能很难直接测量。幸好，爱因斯坦已经给我们指出了物体的能量与它的质量的关系，即
\[E = m{c^2}\]
单个的质子、中子的质量已经精确测定。用质谱仪或其他仪器测定某种原子核的质量，与同等数量的质子、中子的质量之和相比较，看一看两条途径得到的质量之差，就能推知原子核的结合能。
【例题】
已知中子的质量 mn 为 1.674 9×10−27 kg，质子的质量 mp 为 1.672 6 ×10−27 kg，氘核的质量 mD 为 3.343 6×10−27 kg，求氘核的比结合能。
分析 氘核是由 1 个质子和 1 个中子凭借核力结合在一起的，要把它们分开，需要吸收能量，这个能量就是氘核的结合能。由氘核的质量与同等数量的核子质量之间的差值就可以求出与这一质量亏损相对应的能量，再根据氘核的核子数求出氘核的比结合能。
解 单个的质子与中子的质量之和为
\[{m_{\rm{p}}} + {m_{\rm{n}}} = (1.6726 + 1.6749) \times {10^{ - 27}}{\rm{kg = 3}}{\rm{.3475}} \times {10^{ - 27}}{\rm{kg}}\]
这个数值与氘核质量之差
\[\Delta m = ({m_{\rm{p}}} + {m_{\rm{n}}}) - {m_{\rm{D}}} = (3.3475 - 3.3436) \times {10^{ - 27}}{\rm{kg = 3}}{\rm{.90}} \times {10^{ - 30}}{\rm{kg}}\]
与这个质量差相对应的能量为
\[\Delta E = \Delta m{c^2} = 3.90 \times {10^{ - 30}} \times {(3 \times {10^8})^2}{\rm{J}} = 3.51 \times {10^{ - 13}}{\rm{J}}\]
在核物理中，能量单位常常使用电子伏特（eV），即
\[{\rm{1eV = 1}}{\rm{.60}} \times {\rm{1}}{{\rm{0}}^{ - 19}}{\rm{J}}\]
所以，氘核的结合能是
\[\Delta E{\rm{ = }}\frac{{3.51 \times {{10}^{ - 13}}}}{{1.60 \times {{10}^{ - 19}}}}{\rm{eV}} = 2.19 \times {10^6}{\rm{eV}} = 2.19{\rm{MeV}}\]
氘核的比结合能为
\[\frac{{2.19{\rm{MeV}}}}{2} = 1.10{\rm{MeV}}\]
通过这个例题可以看出，原子核的质量小于组成它的核子的质量之和，这个现象叫作质量亏损（mass defect）。质量亏损表明，的确存在着原子核的结合能。
不同原子核的比结合能是不一样的，图 5.3–4 是按照实际测量结果画的图线。可以看出，中等大小的核的比结合能最大（平均每个核子的质量亏损最大），这些核最稳定。
练习与应用
本节共 6 道习题。第 1 题要求学生能够从人工转变与衰变的物理意义和核反应方程两个方面出发，全面认识核反应与化学反应的根本区别，加强学生思考、理解能力的锻炼。第 2 题要求学生理解结合能与比结合能的概念，知道比结合能的大小才是决定原子核稳定程度的因素。第 3 题也是考查对概念的理解，学生需知道宏观与微观的不同，能够区分不同类型的能量及能量转化。第 4、5、6 题旨在通过简单的计算，加深学生对于质能方程的理解。
1．从以下几个方面比较核反应与化学反应的相同和相异之处。
（1）它们各自涉及四种基本相互作用中的哪一种？
（2）每种反应分别改变了或重新安排了什么？
2．为什么原子核的比结合能越大，原子核越稳定？
3．生活中，我们常能看到物体的能量发生了变化，为什么觉察不到物体质量发生的变化？
4．原子物理中常把碳 12 原子质量的 \(\frac{1}{{12}}\) 叫作“原子质量单位”，用 1 u 表示（1 u ＝ 1.660 6×10−27 kg）。
请根据 E = mc2 证明：1 u 相当于 931.5 MeV 的能量。已知光速 c 为 2.997 9×108 m/s，元电荷 e 为 1.602 2×10−19 C。
5．印刷“两弹一星”这四个字的油墨的质量大约是 1 μg（10−9 kg）。与这些质量相当的能量如果完全用来增加重力势能，它可以使一架本身质量 6 000 kg、载有 60 名体重 50 kg 学生的直升机升高多少？
6．一个铀核衰变为钍核时释放一个 α 粒子。在这个衰变过程中释放的能量等于多少焦耳？已知铀核的质量为 3.853 131×10−25 kg，钍核的质量为 3.786 567×10−25 kg，α 粒子的质量为 6.646 72×10−27 kg。
[1] 1967 年，美国物理学家温伯格和巴基斯坦物理学家萨拉姆在美国物理学家格拉肖前期工作的基础上提出了电弱统一理论，把电磁相互作用和弱相互作用统一成了一种相互作用。他们三人因此获得了 1979 年的诺贝尔物理学奖。
第 3 节 核力与结合能 教学建议
1．教学目标
（1）知道四种基本相互作用，知道核力的性质。
（2）认识原子核的结合能和比结合能的概念。
（3）能用质量亏损和质能方程计算核能相关的问题。
2．教材分析与教学建议
本节教科书是在学生已经学习了原子核是由质子和中子组成的基础上，探究是什么作用使质子和中子可以有机地组成一个稳定的整体。为此，教科书首先安排了“核力与四种基本相互作用”，阐明万有引力、电磁力和核力分别在不同的尺度上发挥作用。在教授这部分内容时，应注意引导学生，突出科学家的大胆“猜想”在研究中的作用。
原子核是核子凭借核力结合在一起的，核子结合成原子核会释放能量。从力的角度认识原子核后，要把核子分开，需要提供能量来克服核力所做的功。结合能的教学实际上是从能量的角度再次认识原子核，结合能和比结合能的概念是本章重要的基础知识。注意结合本节教科书中的“思考与讨论”栏目，讲清楚其物理意义。
（1）问题引入
教科书“问题”栏目提出在原子核中是什么力量把带正电的质子紧紧地束缚在一起而不飞散开的问题。在 20 世纪初，人们知道自然界存在万有引力和电磁力，在相同的距离上，质子间的电磁力大约要比万有引力强 1036 倍！原子核中质子间的万有引力根本无法与库仑斥力相比，似乎质子与质子团聚在一起是不可能的。科学家猜想，要形成稳定的原子核，核内部是不是存在更强的第三种力呢？这个问题情境的设计对培养学生提出问题的能力是有益的。
（2）核力与四种基本相互作用
四种基本相互作用分别是：引力相互作用、电磁相互作用、强相互作用和弱相互作用。后两种只能在微观领域（原子核的尺度 10−15 m 范围内）发挥作用，它们都是短程力。弱相互作用的力程比强相互作用更短，为 10−18 m。
教学中以教师讲授为主，同时引导学生自主学习，培养学生的自学能力，通过讨论，激发学习兴趣。
教学片段
核力与四种基本相互作用
知识回顾 让学生从熟悉的库仑定律和万有引力定律出发，比较氦原子核中两个质子之间的库仑斥力与万有引力的大小。已知质子质量 mp 为 1.67×10−27 kg，电荷量为 1.6×10−19 C，原子核的直径的数量级为 10−15 m。通过计算，比较结果，让学生产生强烈的认知冲突，为引入核力的概念奠定基础。
提出问题 在原子核内部的狭小空间，共存有质子和中子。原子核中的质子靠万有引力来抗衡相互间大得多的库仑斥力是不可能的。那么，是什么作用使质子能够在原子核内共存？
科学猜想 科学家猜想，原子核内的核子间很可能存在第三种相互作用强大的核力。正是这种强大的核力把核子紧紧地束缚在原子核的范围内，形成稳定的原子核。后来，科学家的猜想得到了实验的验证。
阅读归纳 引导学生阅读教科书关于核力和四种基本相互作用的内容，讨论、总结并回答核力的特点以及四种基本相互作用在不同尺度上发挥的作用。
核力：
- 核力是强相互作用；
- 核力是短程力，作用范围只有约 10−15 m；
- 相邻的质子之间、中子之间、中子和质子之间都存在核力。
四种基本相互作用：
- 万有引力把行星和恒星聚在一起组成太阳系、银河系和其他星系，决定着宇宙的现状；
- 电磁力在原子核外，电磁力使电子不脱离原子核而形成原子，使原子结合成分子，使分子结合成液体和固体等；
- 强相互作用在原子核内，核力将核子束缚在一起；
- 弱相互作用是引起原子核 β 衰变的原因。
科学探索 人们对于核力的了解还很不够，尤其是小于 0.8×10−15 m 时的核力的变化规律还不清楚，有待于后人们的进一步研究……
（3）结合能
结合能这部分内容的教学可按照教科书中提供的线索进行，要拆散原子核，必须赋予原子核能量，这个能量就是原子核的结合能。这个能量也等于核子结合成原子核而释放的能量。千万不能把结合能理解为“原子核具有的能量”！如何求出结合能呢？利用质能方程即可计算。
教学中应注意一定的质量 m 和一定的能量 mc2 相对应的观点，以及原子核在变化时，其变化前后的总质量是不同的，这种质量的差异对应的就是核反应中所吸收或释放的能量。还应注意向学生说明，原子核反应中的质量亏损并不破坏质量守恒定律，因为质量、能量是物质存在的两种不同的表现形式，一定的质量和一定的能量相对应。
在核能的计算中，要注意训练学生进行单位的换算。例如，原子质量单位和千克的关系，焦耳和电子伏特的关系。
讲清比结合能的概念，使学生知道比结合能越大，意味着把同样数量的核子分开所需要的能量越大，说明核子的结合越牢固，原子核越稳定。一般来说，我们并不关心结合能的绝对大小，而是关心它的变化。发生核反应，从一种原子核变成另一种原子核时，结合能会发生变化。比如，由结合能小的原子核变成结合能大的原子核，就有可能有能量释放出来。这种在核反应中释放出来的能量就是人们通常所说的核能，而改变原子核就是人们获取核能的基本途径。
教学片段
结合能的概念
宏观模型 相距很远的两个物体，由于万有引力而相互接近，运动速度越来越大，引力势能转化为动能。最后撞在一起，一部分动能变成热并散失掉了。两个物体为了结合而付出了代价——失去了一些能量，如果要把它们分开，还要重新赋予它们能量。
微观模型 如果要把原子核中的两个核子分开，可用什么办法？把核子分开需要的能量与核子结合放出的能量有什么关系？
类比分析 可以类比上述分开两个物体的方法，给原子核某种能量。
例如，用 γ 光子照射氘核，可以使它分解为一个质子和一个中子。从实验知道，只有当光子能量等于或大于 2.22 MeV 时，这个反应才会发生。相反的过程是一个质子和一个中子结合成氘核，要放出 2.22 MeV 的能量，这个能量以 γ 光子的形式辐射出去。
再如，如果要让氢原子核的核外电子电离，即从氢原子中把电子剥离，需要让它得到 13.6 eV 的能量。这个能量实际上就是电子与氢原子核的“结合能”，不过通常把它叫作氢原子的电离能，而结合能一词只用在原子核中。
（4）质量亏损
一定的质量总跟一定的能量对应，核子在结合成原子核时总质量减少了，相应的总能量也要减少。根据能量守恒定律，减少的这部分能量不会凭空消失，它要在核子结合时释放出去。反过来，把原子核分裂成核子，总质量要增加，总能量也要增加，增加的能量要由外部供给。在核反应中往往伴随巨大的能量释放或吸收现象。
原子核的质量亏损并不破坏质量守恒定律。例如，在核反应 10n + 11H → 21H + γ 中，以 γ 辐射的形式释放能量，它的能量与氘核的质量亏损相当。
教科书设计的例题可以帮助学生切实体会到什么叫质量亏损，体会利用质能方程计算核能的方法，加深对结合能和比结合能的理解。
分析完例题后，可顺利过渡到对教科书图 5.3–4 原子核的比结合能的处理。该图是由实际测量结果画出的比结合能随质量数变化的图像，分析它可以清楚地看到，中等大小的核的比结合能最大，这说明中等大小的核最稳定。
3．“练习与应用”参考答案与提示
本节共 6 道习题。第 1 题要求学生能够从人工转变与衰变的物理意义和核反应方程两个方面出发，全面认识核反应与化学反应的根本区别，加强学生思考、理解能力的锻炼。第 2 题要求学生理解结合能与比结合能的概念，知道比结合能的大小才是决定原子核稳定程度的因素。第 3 题也是考查对概念的理解，学生需知道宏观与微观的不同，能够区分不同类型的能量及能量转化。第 4、5、6 题旨在通过简单的计算，加深学生对于质能方程的理解。
1．（1）核反应涉及四种基本相互作用力中的强相互作用和弱相互作用；化学反应涉及四种基本相互作用力中的电磁相互作用。
（2）核反应改变了原子核；化学反应可以改变核外电子的排列，从而改变分子结构。
2．结合能是为了把原子核中的核子分开所需要的能量，不同的原子核的核子个数不同，核子数多的结合能会高些；而比结合能是平均到一个核子所需要的能量，比结合能越大，说明平均每个核子所需的能量都要多些，所以分开这种原子核更加困难，这种原子核更加稳定。
3．如果从原子核的核能变化去考虑，就要用到质能关系 ΔE = Δmc2。由于光速很大，我们通常看到的物体能量的变化量对应的质量的变化量就很小，因此我们觉察不到质量发生变化。
4．将题中所给的数据代入公式 E = mc2，得 E = 1.6606×10−27×（2.9979×108）2 J = 1.492 4×10−10 J = 931 MeV。
5．1.02×103 m
提示：1 μg 的质量对应的能量为 E = mc2 =1×10−9×（3×108）2 J = 9×107 J。载有学生的直升机升高的高度为 h = \(\frac{E}{{({m_1} + {m_2})g}}\) = \(\frac{{9 \times {{10}^7}}}{{(3000 + 6000) \times 9.8}}\) = 1.02×103 m。
6．8.352×10−13 J
提示：衰变前后亏损的质量为 Δm =（3.853 13×10−25 −3.786 57×10−25 – 6.646 72×10−27）kg = 0.000 092 8×10−25 kg。释放的能量为 ΔE = Δmc2 = 0.000 092 8×10−25×（3×108）2 J = 8.352×10−13 J。
发布时间：2021/2/2 下午9:41:45 阅读次数：5152
