“复习与提高”参考答案与提示

A 组共 8 道习题。第 1 题考查气体压强的产生。第 2、3 题考查玻意耳定律的应用，其中第 3 题还涉及不同情况下汽缸内气体压强的计算。第 4 题考查盖—吕萨克定律的应用以及查理定律的微观解释。第 5 题考查盖—吕萨克定律的应用。第 6 题考查查理定律的应用。第 7 题结合 p–T 图像对盖—吕萨克定律、查理定律进行综合考查。第 8 题考查对毛细现象的解释。

B 组共 7 道习题。第 1 题通过制作测温装置考查查理定律的应用，对学生能力要求较高。第 2 题考查玻意耳定律在实际生活中的应用。第 3 题结合玻意耳定律测量固体的密度。第 4 题结合查理定律计算轮胎的胎压。第 5 题一方面考查 V–T 图像和 p–T 图像的转换，另一方面考查查理定律和盖—吕萨克定律的综合应用。第 6、7 题考查玻意耳定律，其中第 7 题侧重定性分析。

A 组

1．有。气体压强是气体分子频繁碰撞容器壁产生的，它与气体是否失重无关，完全失重时气体对器壁仍有压强。打足气的篮球在自由下落过程中不会被大气压压瘪（忽略空气阻力的影响）。

 

2．0.44 m

提示：设大气压为 p₀，细管的横截面积为 S，对于封闭在细管中的空气柱，刚进水时长度为 l₁，停止进水时长度为 l₂。由玻意耳定律，有 p₀l₁S = pl₂S。考虑液体的压强，有 p = p₀ + ρgΔh，联立以上两式，代入数据，解得 Δh = \(\frac{5}{{12}}\) m = 0.42 m。则洗衣缸内水位高 h = l₁ – l₂ + Δh = 0.44 m。

 

3．\(\frac{{{ p_0}{l_0}S}}{{{p_0}S - mg}}\)

提示：对于缸内的理想气体，平放时为初态，有 p₁ = p₀，V₁ = l₀S；悬挂时为末态，对缸体有 mg + p₂S = p₀S，即 p₂ = p₀ – \(\frac{{mg}}{S}\)，V₂ = lS。根据玻意耳定律 p₁V₁ = p₂V₂，得 p₀l₀S = (p₀ – \(\frac{{mg}}{S}\)) lS，则气柱长度 l = \(\frac{{{p_0}{l_0}S}}{{{p_0}S - mg}}\)。

 

4．（1）0.4 m³

（2）微观原因：气体体积不变，分子数密度不变，温度降低，气体分子平均动能减小，导致气体压强减小。

提示：设气体在 B 状态时的体积为 V_B，由盖-吕萨克定律，有 \(\frac{{{V_A }}}{{{T_A}}}\) = \(\frac{{{V_B}}}{{{T_B}}}\)，代入数据，解得 V_B = 0.4 m³。

 

5．\(\frac{29}{{30}}\)

提示：设上午 8 时教室内的空气质量为 m，下午 2 时教室内的空气质量为 mʹ。以上午8时教室内的空气为研究对象，由盖-吕萨克定律，有 \(\frac{{{V_1}}}{{{T_1}}}\) = \(\frac{{{V_2}}}{{{T_2}}}\) ，则 V₂ = \(\frac{{{T_2}}}{{{T_1}}}\)V₁ = \(\frac{273+27}{{273+17}}\)V₁ = \(\frac{30}{{29}}\)V₁，所以 \(\frac{{m'}}{m}\) = \(\frac{{{V_1}}}{{{V_2}}}\) = \(\frac{29}{{30}}\)。

 

6．150.5℃

提示：不锈钢碗里的气体，发生等容变化。

初态：p₁ = p₀ = 1.0×10⁵ Pa，T₁ = t + 273 K（t 为两个不锈钢碗刚扣上时里面空气的温度）；

末态：碗内压强为 p₂，T₂ = 288 K。

对一个碗进行受力分析可知 p₀S = p₂S + 5F，代入数据，解得 p₂ = 0.68×10⁵ Pa。

由查理定律，有 \(\frac{{{p_1}}}{{{T_1}}}\) = \(\frac{{{p_2}}}{{{T_2}}}\)，代入数据，解得 t = 150.5℃。

 

7．270 K

提示：气体从状态A 到 状态 B 压强不变，由盖—吕萨克定律，有 \(\frac{{{V_A}}}{{{T_A}}}\) = \(\frac{{{V_B}}}{{{T_B}}}\)，其中 \(\frac{{{V_B}}}{{{V_A}}}\) = \(\frac{3}{{1}}\)，得 T_B = \(\frac{{{V_B}}}{{{V_A}}}\)T_A = 900 K。

气体从状态 B 到状态 C 体积不变，由查理定律，有 \(\frac{{{p_B}}}{{{T_B}}}\) = \(\frac{{{p_C}}}{{{T_C}}}\)，其中 \(\frac{{{p_C}}}{{{p_B}}}\) = \(\frac{3}{{10}}\)，得 T_C = \(\frac{{{p_C}}}{{{p_B}}}\)T_B = 270 K。

 

8．土壤里有很多毛细管，地下水分可以沿着它们上升到地面。翻松土壤可以破坏土壤里的毛细管，从而防止土壤中的水分散失。

B 组

1．（1）22 cm        （2）高；由于实际压强小，根据查理定律可知实际温度低，所以显示温度比实际温度高。

提示：选玻璃泡 A 内的气体为研究对象，温度变化时，A 内气体经历了一个等容过程。根据题意可知，初态温度 T₁ 为 300 K，压强 p₁ 相当于（76 − 16）cm 水银柱产生的压强；末态温度 T₂ 为 270 K，设压强为 p₂。则根据查理定律 \(\frac{{{p_1}}}{{{T_1}}}\) = \(\frac{{{p_2}}}{{{T_2}}}\)，代入数据，解得 p₂ 相当于 54 cm 水银柱产生的压强，所以 x =（76 − 54）cm = 22 cm。

 

2．先将吸盘紧压在墙壁上，使吸盘中的空气排出一部分。扳下锁扣，吸盘被向外拉出，吸盘内气体体积变大，压强减小。松手后，吸盘内部压强小于外界大气压，这样，盘盖就会对吸盘边缘产生很大的压力，使吸盘边缘贴紧墙面，防止空气渗入吸盘内部。

 

3．77.7 cm³

提示：设水银密度为 ρ，大气压为 p₀，容器 B 的体积为 V_B，固体体积为 V。

以 C、A、B 中封闭气体为研究对象，以封闭时水银面位于 n 处为初状态，以水银面调至 m 处为末状态。由玻意耳定律，有 p₀（V_B + V_C）=（p₀ + ρgh₁）V_C。

以 C 中放入固体后 C、A、B 中气体为研究对象，同理，有 p₀（V_B + V_C − V）=（p₀ + ρgh₂）（V_C − V）。

代入数据，解得 V = 77.7 cm³。

 

4．2.032×10⁵ ~ 2.777×10⁵ Pa

提示：由于轮胎容积不变，故轮胎内气体发生等容变化。设在 T₀ = 293 K 充气后的最小胎压为 p_min，最大胎压为 p_max。

根据题意，当 T₁ = 233 K时，胎压 p₁ = 1.616×10⁵ Pa，由查理定律，有 \(\frac{{{p_1}}}{{{T_1}}}\) = \(\frac{{{p_{\min}}}}{{{T_0}}}\)，代入数据，解得 p_min = 2.032×10⁵ Pa；当 T₂ = 373 K时，胎压 p₂ = 3.535×10⁵ Pa，由查理定律，有 \(\frac{{{p_2}}}{{{T_2}}}\) = \(\frac{{{p_{\max}}}}{{{T_0}}}\)，代入数据，解得 p_max = 2.777×10⁵ Pa。

故充气后的胎压在 2.032×10⁵ ~ 2.777×10⁵ Pa 比较合适。

 

5．如图 2–11 所示。

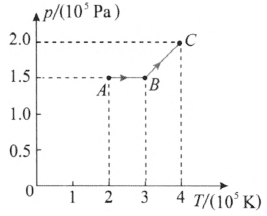
提示：从题图可以看出，A 与 B 连线的延长线经过原点，所以从 A 到 B 是等压变化，即p_A = p_B，由盖-吕萨克定律，有 \(\frac{{{V_A}}}{{{T_A}}}\) = \(\frac{{{V_B}}}{{{T_B}}}\)，得 T_A = \(\frac{{{V_A}}}{{{V_B}}}\)T_B = ×300 K = 200 K；从 B 到 C 是等容变化，由查理定律，有 \(\frac{{{p_B}}}{{{T_B}}}\) = \(\frac{{{p_C}}}{{{T_C}}}\)，得 p_C = \(\frac{{{T_C}}}{{{T_B}}}\)p_B = ×1.5×10⁵ Pa = 2.0×10⁵ Pa。

由此可画出由 A 到 B 到 C 的 p–T 图像，如图 2–11 所示。

 

6．27.5 cm

提示：以玻璃管中封闭的空气为研究对象，它经历等温变化。设水银的密度为 ρ，玻璃管的横截面积为 S，大气压为 p₀（相当于 76 cm 水银柱产生的压强）。

开口向下时：p₁ = p₀ − ρgl₀，V₁ = l₁S；

水平放置时：p₂ = p₀，V₂ = l₂S；

开口向上时：p₃ = p₀ + ρgl₀，V₃ = l₃S；

由玻意耳定律，有 p₁V₁ = p₂V₂ = p₃V₃，代入数据，解得 l₃ = 27.5 cm。

 

7．将玻璃管往下压一点后，玻璃管中的空气体积会减小，压强会变大，管内气体给玻璃管向上的压力会大于玻璃管所受的重力，故管会返回原来的平衡位置。