第二章 4 固体

问题 ？

观察食盐颗粒和松香的外形，它们的外形各有怎样的特征？

再用显微镜观察精盐和松香粉末的外形，两者有什么样的差别吗？

食盐颗粒总是呈现立方体形，松香颗粒没有规则的几何形状。

晶体和非晶体

固体可以分为晶体和非晶体两类。

石英、云母[1]、明矾、食盐、硫酸铜、味精等是晶体。

雪花是水蒸气凝华时形成的晶体，它们都具有相似的几何形状，即图案中都有六个角（图2.4-1）。食盐晶体是正六面体形，明矾晶体总是八面体形，天然石英晶体（俗称水晶）的中间是一个六棱柱，两端是六棱锥（图2.4-2）。晶体有天然的、规则的几何形状（图2.4-3）。

玻璃、蜂蜡、松香、沥青、橡胶等是非晶体。非晶体没有规则的外形。

除了形状是否规则外，晶体和非晶体在物理性质上也有所不同。我们在初中已经学过，晶体具有确定的熔点，非晶体没有确定的熔化温度，这就是区别之一。此外，其他物理性质也有差异。

实验

观察玻璃和云母片上石蜡熔化区域的形状

把熔化了的石蜡薄薄地涂在薄玻璃片和单层云母片上，再将烙铁通电烧热，然后用烙铁头分别接触玻璃片和云母片的背面（图 2.4-4）。观察玻璃片和云母片石蜡熔化区域的形状（图 2.4-5）。

石蜡熔化区域形状的不同说明了什么？

从实验结果可以看出，玻璃片上石蜡熔化区域的形状近似于圆形，表明玻璃沿各个方向的导热性能相同；云母片上石蜡熔化区域的形状呈椭圆形，表明云母沿不同方向的导热性能不同。还有些晶体沿不同方向的导电性能不同；而有些晶体沿不同方向的光学性质不同，这类现象叫作各向异性（anisotropy）。如图2.4-6，方解石晶体是各向异性的晶体，它能把光分解为两束光而沿不同方向折射，形成双折射现象。非晶体沿各个方向的物理性质都是一样的，这叫作各向同性（isotropy）。

思考与讨论

常见的金属没有规则的形状，但具有确定的熔点。它们是晶体还是非晶体？

从金属的显微图样中可以看到，它是由许多细小的晶粒组成的（图2.4-7）。每个晶粒都是一个小的单晶体（monocrystal），有规则的形状且各向异性。

但是，由于这些小的单晶体的取向杂乱无章，所以金属没有确定的几何形状，也不显示各向异性，仅保留了在一定压强下具有确定熔点的特征，我们把它称为多晶体（polycrystal）。蔗糖受潮后粘在一起形成的糖块，看起来没有确定的几何形状。但是用放大镜观看，仍可以发现组成糖块的一个个晶体粒。粘在一起的糖块也是多晶体，单个的蔗糖晶体颗粒是单晶体。

晶体的微观结构

为什么晶体的形状和物理性质会与非晶体不同？

人们认为很可能是它们的微观结构不一样。从17世纪到19世纪，陆续出现了一些假说，某一种假说认为各种晶体内部的微粒是按各自的规则排列着的，但是，由于当时检测技术的限制，缺少实验证据，所以，这些想法只能是假说。

到了20世纪初，通过X射线在晶体上衍射的实验，这种假说才得到证实。在20世纪70年代，人们又用电子显微镜观察到了铀、钍原子的像。1982年，人们用扫描隧道显微镜观察到物质表面原子的排列。

在各种晶体中，原子（或分子、离子）都是按照一定的规则排列的，具有空间上的周期性。图2.4-8是食盐晶体中氯离子和钠离子分布的示意图。

有的物质在不同条件下能够生成不同的晶体。那是因为组成它们的微粒能够按照不同规则在空间分布。例如，碳原子如果按图2.4-9那样排列，就成为石墨，而按图2.4-10那样排列，就成为金刚石。石墨是层状结构，层与层之间距离较大，原子间的作用力比较弱，所以，石墨质地松软，可以用来制作粉状润滑剂；金刚石中碳原子间的作用力很强，所以，金刚石有很大的硬度，可以用来切割玻璃。

原子（或者分子、离子）并不是静止不动的。它们在不停地振动，图中所画的那些点，是它们振动的平衡位置。

同种物质也可能以晶体和非晶体两种不同的形态出现，也就是说，物质是晶体还是非晶体，并不是绝对的。例如，天然石英是晶体，而熔化以后再凝固的水晶（即石英玻璃）就是非晶体 （图2.4-11）。有些非晶体在一定条件下也可以转化为晶体。

科学漫步

石墨烯实验研究背后的故事

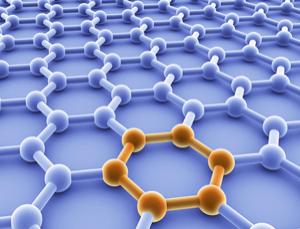
我们知道，物体是由原子、分子等微粒组成的，它们按一定规律组成一个个“小单元”，这些“小单元”结合在一起形成了肉眼可见的物体。用机械的方法把物体粉碎、研磨，可以得到很细的粉末，但实际上一粒这样的粉末仍比这里说的“小单元”大得多。当构成材料的“小单元”的某个维度达到纳米尺度时，它的性质就会发生很大的变化。石墨烯就是一个典型的例子。

石墨烯具有六边形的晶格结构（图2.4-12），单层厚度仅为0.335 nm。2010年的诺贝尔物理学奖授予了安德烈·盖姆与康斯坦丁·诺沃肖洛夫两人，以表彰他们对石墨烯的开创性实验研究。

安德烈对待研究工作一直颇具想象力和好奇心。例如，他在利用超导强磁铁发现水分子具有抗磁性后（水滴悬浮在磁场中），便开始思考：生物体内绝大多数物质是水，而且生物体内的蛋白质也具有抗磁性，如果将生物体放入磁场内，会像水滴一样悬浮吗？于是，他把一只活体青蛙放入磁场，在精确的计算下，这只青蛙真的悬浮在了磁场中。安德烈将这个实验结果发表在了物理期刊上，并为他赢得了2000年的“搞笑诺贝尔物理学奖”。然而，他的想象力并未止步，也从未停止……

在2004年之前，人类对材料的研究已经进入纳米、甚至原子尺度，人们也对石墨烯的结构有了更清晰的认识，预言了单层石墨可能会有非常好的物理性质。但如何把石墨不断磨薄，薄到只有一个原子的厚度，然而，这个世界性难题还是让很多科学家们望而却步了，甚至有人质疑单层石墨是否能够独立存在。安德烈的想象力再一次“拯救”了这项研究，在助手们试图将石墨块磨成石墨烯而陷入“绝境”的时候，安德烈在偶然的机会下，观察到助手们用透明胶带去除石墨块表面的污渍。这时他天才的直觉引导他将粘过的胶带放到仪器下观察，发现远比助手们打磨好的样品薄了许多，有的甚至只有几十个原子那么厚。随即，他便利用透明胶带反复地粘黏，直到获得了单层的石墨——石墨烯。石墨烯独特的结构使得它在力学、电学等方面具有很多奇特的物理性质。

在力学特性方面，石墨烯是目前人类已知的强度最高的物质之一。强度比世界上最好的钢铁还要高百倍之多。同时还具有很好的韧性，且可以弯曲。在电学、热学特性方面，电子在石墨烯中“奔跑”的速率（即迁移率）比在硅材料中高出数十倍甚至上百倍，这有利于进一步提高计算机处理器的运算速率。

无论是搞笑的，还是货真价实的诺贝尔物理学奖，安德烈的研究总是让人颇感意外。解决具有挑战性的科学问题，除了扎实的理论和精密的仪器外，好奇心、想象力、对日常生活的细致观察和灵活运用也同样重要。

练习与应用

1．某人为了检验一块薄片物质是否为晶体，做了一个实验。他以薄片的正中央O为坐标原点，建立Oxy平面直角坐标系，在两个坐标轴上分别取两点x₁ 和y₁ ，使x₁ 和y₁ 到O点的距离相等。在x₁ 和y₁ 上分别固定一个测温元件，再把一个针状热源放在O点，发现x₁ 点和y₁ 点的温度在缓慢升高，但两点温度的高低没有差异。于是得出结论：这块薄片是非晶体。

请说明：以上结论科学吗？为什么？

2．食盐晶体的结构可以用钠离子和氯离子空间分布的示意图表示（图2.4-8），图中相邻离子的中心用线连起来了，组成了一个个大小相等的立方体。现在要估算相邻两个钠离子中心的距离，除了知道食盐的密度 ρ 为2.17×10³ kg/m³ 外，还要知道哪些数据？请用字母表示这些已知数据，推导出相邻两个钠离子中心距离的表达式。

提示：图中最小立方体的个数与离子数目相等。

3．内陆盐矿中开采的氯化钠称为岩盐，岩盐的颗粒很大，我们能清楚地看出它的立方体形状。把大颗粒的岩盐敲碎后，小颗粒的岩盐仍然呈立方体形状。

图2.4-13表示了岩盐晶体的平面结构：粉红点为氯离子，灰点为钠离子，如果把它们用直线连起来，将构成一系列大小相同的正方形，作分界线AA₁，使它平行于正方形的对角线，作分界线BB₁，使它平行于正方形的一边。在两线的左侧各取一个钠离子M和N，为了比较这两个钠离子所受分界线另一侧的离子对它作用力的大小，分别以M、N为圆心，作两个相同的扇形，不考虑扇形以外远处离子的作用。

（1）如果F表示两个相邻离子之间引力的大小，问：M、N所受扇形范围内的正负离子对它作用力的合力是F的多少倍？为使问题简化，设所有离子都是质点，而且它们之间的相互作用遵从“平方反比”规律。

（2）根据计算结果解释：为什么敲碎的岩盐总是呈立方形状，而不会沿图中AA₁分界线断开？

提示：实际晶体中的作用力要复杂得多，但这里的分析对理解自然现象还是有用的。

发布时间：2021/1/11 下午12:32:01  阅读次数：2927