第二章 3 气体的等压变化和等容变化

问题？

烧瓶上通过橡胶塞连接一根玻璃管，向玻璃管中注入一段水柱。用手捂住烧瓶，会观察到水柱缓慢向外移动，这说明了什么？

实验表明，在保持气体的压强不变的情况下，一定质量气体的体积随温度的升高而增大。

气体的等压变化

一定质量的某种气体，在压强不变时，体积随温度变化的过程叫作气体的等压变化。

我们可以用实验研究一定质量的某种气体在压强不变的情况下，其体积V与热力学温度T的关系。实验表明，在V-T 图像中，等压线是一条过原点的直线（图2.3-1）。

法国科学家盖-吕萨克首先通过实验发现了这一线性关系，这个规律可以表述为：一定质量的某种气体，在压强不变的情况下，其体积 V 与热力学温度 T 成正比，即

\(V = CT\)                  （1）

其中 C 是常量。或者

\[\frac{{{V_1}}}{{{T_1}}} = \frac{{{V_2}}}{{{T_2}}}\] 

其中 V₁ 、T₁ 和 V₂ 、T₂ 分别表示气体在不同状态下的体积和热力学温度。（1）式反映了一定质量的某种气体的等压变化规律，我们把它叫作盖-吕萨克定律（Gay-Lussac law）。

气体的等容变化

一定质量的某种气体，在体积不变时，压强随温度变化的过程叫作气体的等容变化。

图2.3-2是气体等容变化时压强与温度的关系图像。从图2.3-2甲可以看出，在等容变化过程中，压强p与摄氏温度t是一次函数关系，不是简单的正比例关系。但是，如果把直线AB延长至与横轴相交（图2.3-2乙），把交点作为坐标原点，建立新的坐标系（图2.3-2丙），那么，这时的压强与温度的关系就是正比例关系了。

法国科学家查理在分析了实验事实后发现，当一定质量的气体体积一定时，各种气体的压强与温度之间都有线性关系。

可以证明，气体的压强不太大、温度不太低时，图 2.3-2 丙中坐标原点代表的温度就是热力学温度的 0 K，也称绝对零度。所以说，在 p–T 图像中，一定质量的某种气体的等容线是一条通过坐标原点的直线。这时，这个规律可以表述为：一定质量的某种气体，在体积不变的情况下，压强p 与热力学温度 T 成正比，即 p ∝ T。写成等式的形式就是

\(p = CT\)                      （2）

其中 C 是常量。或者

\[\frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}}\]

其中 p₁ 、T₁ 和 p₂ 、T₂ 分别表示气体在不同状态下的压强和热力学温度。（2）式反映了一定质量的某种气体的等容变化规律，我们把它叫作查理定律（Charles law）。

在我们的计算中，相当于大气压几倍的压强都可以算作“压强不太大”，零下几十摄氏度的温度也可以算作“温度不太低”。

【例题】

某种气体的压强为 2×10⁵ Pa，体积为 1 m³ ，温度为 200 K。它经过等温过程后体积变为 2 m³ 。随后，又经过等容过程，温度变为 300 K，求此时气体的压强。

分析 封闭容器中的气体，在状态变化中气体质量不变。气体开始时的压强、体积和温度分别为 p₁、V₁、T₁ ，经过等温过程变为 p、V、T，再经过等容过程变为 p₂、V₂ 、T₂ 。我们可以分别运用玻意耳定律和查理定律求解。

解 根据玻意耳定律，有

\[{T_1} = T,{p_1}{V_1} = pV\]

根据查理定律，有

\[V = {V_2},\frac{p}{T} = \frac{{{p_2}}}{{{T_2}}}\]

联立上述各式可得

\[\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\]

\[{p_2} = \frac{{{p_1}{V_1}{T_2}}}{{{V_2}{T_1}}} = \frac{{2 \times {{10}^5} \times 1 \times 300}}{{2 \times 200}}{\rm{Pa}} = 1.5 \times {10^5}{\rm{Pa}}\]

等温和等容变化后气体的压强为 1.5×10⁵ Pa。

理想气体

前面学习的等温、等压和等容三个气体实验定律都是在压强不太大（相对大气压）、温度不太低（相对室温）的条件下总结出来的。当压强很大、温度很低时，由上述规律计算的结果与实际测量结果有很大的差别。例如，有一定质量的氦气，压强与大气压相等，体积为 1 m³ ，温度为0 ℃。在温度不变的条件下，如果压强增大到大气压的 500 倍，按气体的等温变化规律计算，体积应该缩小至\(\frac{1}{{500}}\)m³，但是实验结果是\(\frac{1.36}{{500}}\) m³ 。但是，在通常的温度和压强下，很多实际气体，特别是那些不容易液化的气体，如氢气、氧气、氮气、氦气等，其性质与实验定律的结论符合得很好。

实际气体的分子之间有相互作用力，但是作用力很小；分子也有大小，但气体分子之间的间距比分子直径大得多；气体分子与器壁碰撞几乎是完全弹性的，动能损失也很小。为了研究方便，我们设想有一种气体：这种气体分子大小和相互作用力可以忽略不计，也可以不计气体分子与器壁碰撞的动能损失。这样的气体在任何温度、任何压强下都遵从气体实验定律，我们把它叫作理想气体（ideal gas）。按照这种理想情况下得出的物理规律能很好地解释实际气体的热学性质。在温度不低于零下几十摄氏度、压强不超过大气压的几倍时，把实际气体当成理想气体来处理，误差很小。

拓展学习

理想气体的状态方程

描述一定质量的某种理想气体状态的参量有三个，即压强p、体积V和温度T。等温、等压和等容三个实验定律都是研究当一个参量不变时另外两个参量的关系问题。进一步的研究结果表明，一定质量的某种理想气体，在从某一状态变化到另一状态时，尽管其压强p、体积V和温度T都可能改变，但是压强p跟体积V的乘积与热力学温度T的比值却保持不变。也就是说

\[\frac{{pV}}{T} = C\]

式中C 是与压强p、体积V、温度T无关的常量，它与气体的质量、种类有关。上式叫作理想气体的状态方程。

气体实验定律的微观解释

用分子动理论可以定性解释气体的实验定律。

一定质量的某种理想气体，温度保持不变时，分子的平均动能是一定的。在这种情况下，体积减小时，分子的数密度增大，单位时间内、单位面积上碰撞器壁的分子数就多，气体的压强就增大（图2.3-3）。这就是玻意耳定律的微观解释。

一定质量的某种理想气体，温度升高时，分子的平均动能增大；只有气体的体积同时增大，使分子的数密度减小，才能保持压强不变。这就是盖-吕萨克定律的微观解释。

一定质量的某种理想气体，体积保持不变时，分子的数密度保持不变。在这种情况下，温度升高时，分子的平均动能增大，气体的压强就增大。这就是查理定律的微观解释。

科学方法

理想模型

在科学研究中，理想模型是为了便于研究问题而对研究对象进行理想化抽象的过程。实际问题往往比较复杂，影响的因素很多，直接研究它们会比较困难或几乎不能研究。科学研究中总是抓住研究对象的主要特征，忽略次要因素，对研究对象进行理想化抽象。运用这种方法，人们就可以用模型来表示研究对象，使得研究变得简单、有效，从而便于人们去认识和把握问题的本质。应该说，理想模型在现实中并不存在，但是通过它可以对实际问题进行本质探讨，并得到有价值的结论。物理学中通过抽象方法构建的理想化模型有很多，例如，质点、点电荷、单摆、弹簧振子、理想变压器、理想气体等。

练习与应用

1．盛有氧气的钢瓶，在 17 ℃的室内测得钢瓶内的压强是 9.31×10⁶ Pa。当钢瓶搬到－13 ℃的工地上时，瓶内的压强变为 8.15×10⁶ Pa。钢瓶是不是漏气？为什么？

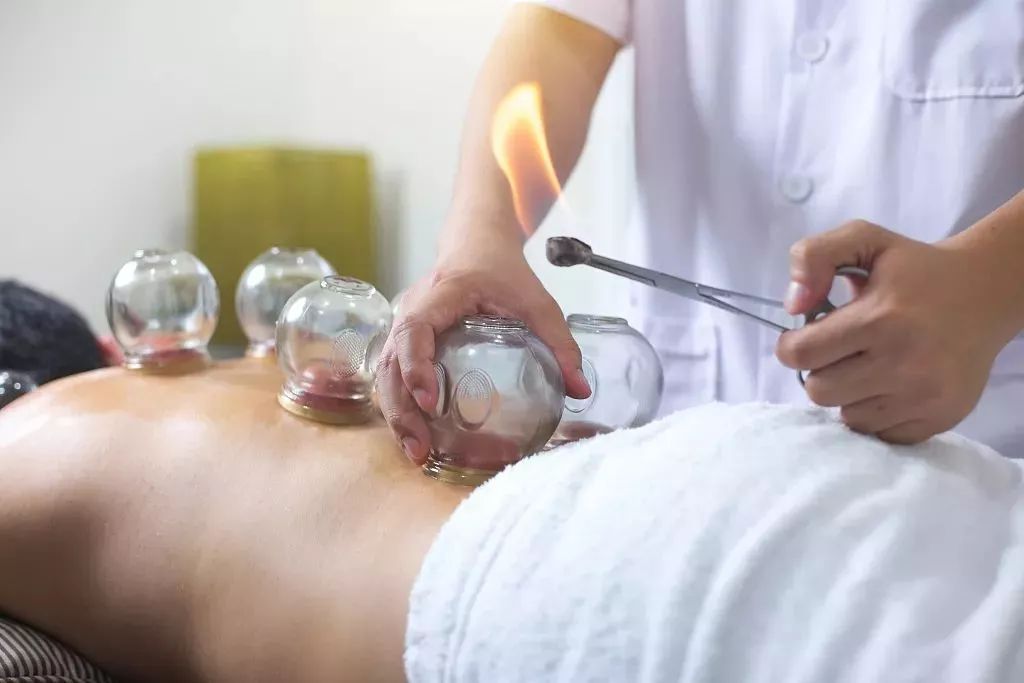
2．“拔火罐”是我国传统医学的一种治疗手段。操作时，医生用点燃的酒精棉球加热一个小罐内的空气，随后迅速把小罐倒扣在需要治疗的部位，冷却后小罐便紧贴在皮肤上（图 2.3-4）。设加热后小罐内的空气温度为 80 ℃，当时的室温为 20 ℃，大气压为标准大气压，小罐开口部位的直径请按照片中的情境估计。当罐内空气变为室温时，小罐对皮肤的压力大概有多大？不考虑因皮肤被吸入罐内导致空气体积变化的影响。

3．如图 2.3-5，向一个空的铝制饮料罐中插入一根透明吸管，接口用蜡密封，在吸管内引入一小段油柱（长度可以忽略）。如果不计大气压的变化，这就是一个简易的气温计。已知罐的容积是 360 cm³ ，吸管内部粗细均匀，横截面积为 0.2 cm² ，吸管的有效长度为 20 cm，当温度为 25 ℃时，油柱离管口 10 cm。若给吸管上标刻温度值，刻度是否均匀？试估算这个气温计的测量范围。

4．一个容器内部呈不规则形状，为测量它的容积，在容器上插入一根两端开口的玻璃管，接口用蜡密封。玻璃管内部横截面积为 S，管内一静止水银柱封闭着长度为 l₁ 的空气柱，如图 2.3-6，此时外界的温度为 T₁ 。现把容器浸在温度为 T₂ 的热水中，水银柱静止时下方的空气柱长度变为 l₂ 。实验过程中认为大气压没有变化，请根据以上数据推导容器容积的表达式。

发布时间：2021/1/10 下午4:42:39  阅读次数：7930