第二章 1 温度和温标
2
第二章
气体、固体和液体
物体是由大量分子组成的,分子在做永不停息的无规则运动,分子之间存在着相互作用力。这些因素决定了分子的三种不同的聚集状态:气体、固体和液体。物体处于不同状态时具有不同的物理性质。
人类对物质属性的认识是从宏观到微观不断深入的过程。相应地,人们对新材料或传统材料新功能的开发和研制也从来没有停止过。从远古的石器时代,到后来的青铜器时代、铁器时代……新材料在人类文明进程中扮演了重要的角色。
要推论宏观物质的表现,就必须采用统计方法,由对个体原子(分子)物理参量的适当统计平均,来得出支配宏观行为的规律。
——彭罗斯①
假如一个容器用挡板 K 隔开,容器中的气体被分成 A、B 两部分,它们的压强分别为 pA 、pB ,温度分别为 TA 、TB 。打开挡板 K 后,如果容器与外界没有能量交换,经过一段时间后,容器内的气体会是什么状态?
研究某一容器中气体的热学性质,其研究对象是容器中的大量分子组成的系统,这在热学中叫作一个热力学系统(thermodynamic system),简称系统。系统之外与系统发生相互作用的其他物体统称外界。例如,用酒精灯加热容器中的气体,把气体作为研究对象,它就是一个热力学系统,而容器和酒精灯就是外界。
在力学中,为描述物体(质点)的运动状态,我们使用了物体的位置和速度这两个物理量。在热学中,为确定系统的状态,也需要用到一些物理量,这些物理量叫作系统的状态参量(state parameter)。例如,为了确定系统的空间范围,要用到体积 V,这是一个几何参量;为了确定外界与系统之间或系统内部各部分之间力的作用,要用到
① 彭罗斯(Roger Penrose,1931 — ),英国数学家、物理学家,2020 年诺贝尔物理学奖获得者,牛津大学教授,著名科普著作《皇帝新脑》的作者。
压强 p,这是一个力学参量;而要确定系统的冷热程度,就要用到一个热学参量——温度 T。
要定量地描述系统的状态往往很难,因为有时系统的参量会随时间变化。然而在没有外界影响的情况下,只要经过足够长的时间,系统内各部分的状态参量能够达到稳定状态。这种状态叫作平衡态(equilibrium state),否则就是非平衡态。当系统处于平衡态时,系统所有状态参量都不随时间变化,我们就能比较准确地描述系统的状态。在中学阶段,我们主要处理平衡态的问题。
上面所说的平衡态,指的是一个系统的状态参量不再改变。下面我们要研究一个系统与另一个系统相互作用的问题。
如果两个系统相互接触而传热,这两个系统的状态参量将会互相影响而分别改变。经过一段时间,各自的状态参量就不再变化了,这说明两个系统达到了平衡。这种平衡叫作热平衡(thermal equilibrium)。
实验表明:如果两个系统分别与第三个系统达到热平衡,那么这两个系统彼此之间也必定处于热平衡,这个结论称为热平衡定律。
热平衡定律表明,当两个系统 A、B 处于热平衡时,它们必定具有某个共同的热学性质,我们就把表征这一“共同的热学性质”的物理量叫作温度(temperature)。换句话说,温度是决定一个系统与另一个系统是否达到热平衡的物理量,它的特点就是“达到热平衡的系统具有相同的温度”(图 2.1–1)。下表列出了部分人们已观测的温度。
如果要定量地描述温度,就必须有一套方法,这套方法就是温标(thermometric scale)。
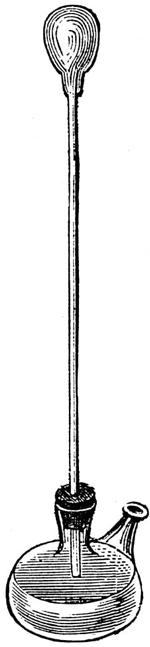
确定一个温标时首先要选择一种测温物质,根据这种物质的某个特性来制造温度计。例如,可以根据水银的热膨胀来制造水银温度计,这时我们规定细管中水银柱的高度与温度的关系是线性关系。还可以根据气体压强随温度的变化来制造气体温度计(图 2.1–2),等等。
确定了测温物质和它用以测温的某种性质之后,还要确定温度的零点和分度的方法。例如,摄氏温标曾经规定,标准大气压下冰的熔点为 0 ℃,水的沸点为 100 ℃;并据此把玻璃管上 0 ℃ 刻度与 100 ℃ 刻度之间均匀分成 100 等份,每份算做 1 ℃。
现代科学中用得更多的是热力学温标。热力学温标表示的温度叫作热力学温度(thermodynamic temperature),它是国际单位制中七个基本物理量之一,用符号 T 表示,单位是开尔文(kelvin),简称开,符号为 K。
1960年,国际计量大会确定了摄氏温标与热力学温标的关系:摄氏温标由热力学温标导出,摄氏温标所确定的温度用 t 表示,它与热力学温度 T 的关系是
\[T = t + 273.15\;{\rm{K}}\]
根据国家标准,在表示温度差的时候可以用摄氏度(℃)代替开尔文(K),即 1℃ 与 1 K 相等。因此这个式子中 T 的单位用 K,t 的单位用 ℃。
形形色色的温度计
自从伽利略制造了第一个温度计以后,温度就不再是一个主观感觉,而成了一个客观的物理量。人们根据物质某种与温度有关的性质制作了多种温度计。例如,双金属温度计是把线膨胀程度不同的两种金属片压合在一起,温度变化时,双金属片的弯曲程度会发生变化,带动指针偏转来指示温度(图2.1–3)。热电偶温度计是根据不同导体因温差而产生电动势的大小不同来制作的。如图2.1–4,把一条金属丝的两端分别与另一条不同材料金属丝的两端熔焊,接成闭合电路,倘若两个焊点之间有温度差,电路中就有电动势产生,温度差越大,电动势也越大。热电偶温度计的测温探头,实际上就是两根金属丝相连的一个焊点。选择不同的金属丝可以做成不同的热电偶温度计,有的可以测量高达 3 000 ℃的高温,有的可以测量接近绝对零度的低温。
电阻温度计是根据金属的电阻率随温度的升高而变化的原理制成的。常见的金属电阻温度计有铂电阻温度计和铜电阻温度计,铂电阻温度计是目前最精确的温度计。热敏电阻温度计是利用某些半导体材料制作的,其电阻随温度的变化比导体更明显,但热敏电阻的稳定性差,主要用于低精度的测量。
压力表式温度计是根据气体压强随温度变化的规律制作的。某些铁磁性物质的磁性强弱跟温度有关,磁性的强弱便可以成为温度的标志。声音的传播速度跟介质的温度有关,声速也可以成为温度的标志。有些晶体(如石英)的固有频率跟温度有关,频率也可以成为温度的标志。根据这个思路,磁温度计、声速温度计、频率温度计等都相继制成,而且发挥着各自的作用。
1.“在测定某金属块的比热容时,先把质量已知的金属块放在沸水中加热。经过一段时间后把它迅速放入质量已知、温度已知的水中,并用温度计测量水的温度。当水温不再上升时,这就是金属块与水的共同温度。根据实验数据就可以计算金属块的比热容。”在这样的叙述中,哪个地方涉及了“热平衡”的概念?
2.天气预报某地某日的最高气温是 27 ℃,它是多少开尔文?进行低温物理的研究时,热力学温度是 2.5 K,它是多少摄氏度?
3.已知某物理量 X 与热力学温度 T 成正比,请把这个关系式用等式表示出来。现在用摄氏温度 t 来表示温度,这个关系式又该怎么写?分别画出 X–-T 图像和 X–t 图像的草图。
4.图 2.1–5 甲表示某金属丝的电阻 R 随摄氏温度 t 变化的情况。把这段金属丝与电池、电流表串联起来(图 2.1–5 乙),用这段金属丝做测温探头,把电流表的电流刻度改为相应的温度刻度,就得到了一个简单的电阻温度计。请判断 :如果电池的电动势和内阻都是不变的,电流表上代表 t1 、t2 的两点,哪个应该标在电流比较大的刻度上?
第二章 气体、固体和液体
课程标准的要求
3.1.3 了解固体的微观结构。知道晶体和非晶体的特点。能列举生活中的晶体和非晶体。通过实例,了解液晶的主要性质及其在显示技术中的应用。
3.1.4 了解材料科学的有关知识及应用,体会它们的发展对人类生活和社会发展的影响。
3.1.5 观察液体的表面张力现象。了解表面张力产生的原因。知道毛细现象。
3.1.6 通过实验,了解气体实验定律。知道理想气体模型。能用分子动理论和统计观点解释气体压强和气体实验定律。
一、本章教材概述
物体是由大量分子组成的,分子永不停息地做无规则运动,分子间存在着相互作用力。这些因素决定了分子的不同聚集状态,也就决定了物质的结构。当分子的无规则运动起主要作用时,物质将呈气体状态;当分子间的作用力起主要作用时,物质将呈固体状态;当分子的无规则运动与分子间的作用力这对矛盾旗鼓相当时,物质将呈液体状态。物质的结构不同,自然表现出不同的物理性质。
本章是在第一章“分子动理论”的基础上,研究物质在不同物态下的一些规律和性质。通过本章的学习,要使学生体会到,分子动理论不仅能从微观角度研究气体,而且能够研究固体和液体。
本章在结构设计方面大致可划分为三个单元。第一单元是第 1 节“温度和温标”,介绍了从宏观角度研究热现象的相关物理概念(系统、系统的状态参量、平衡态、热平衡、判断热平衡的物理量——温度),以及描述测量温度的方法和工具(温标和温度计)。第二单元由第 2 节“气体的等温变化”和第 3 节“气体的等压变化和等容变化”组成,研究了气体在等温、等压和等容的状态下的变化规律,概括得出了理想气体的概念,并在“拓展学习”栏目中介绍了各个状态参量都发生变化时的关系式,即理想气体的状态方程。第三单元由第 4 节“固体”和第 5 节“液体”组成,介绍了从微观角度研究固体和液体的一些性质,如晶体及其微观结构、液体的表面现象和液晶等。
具体来说,在编写本章内容时有以下一些思考。
1.通过初、高中“温度”概念的变化,发展学生的科学思维
初中阶段学生对于温度的认识只是“物体的冷热程度”;高中阶段对温度的认识是从分子动理论的观点出发,给出温度的微观含义,即“温度是物体分子热运动的平均动能的标志”。温度的严格定义及测量原理是建立在热平衡定律基础上的,即“处于热平衡的两个系统具有某个共同的热学性质”。对温度概念认识上的深化,是在研究热现象的相关物理概念作支撑的前提下进行的。在此,我们需要让学生遵循一定的逻辑关系对温度概念有一些初步的科学认识。这样处理的目的是养成学生理性思维的习惯,培养科学思维中的推理、论证能力。关于“温度”概念,教科书的编写思路如下:
教科书中对“平衡态”“热平衡”“温度”“温标”等概念的处理,逻辑关系清晰,同时,要求学生能从“动”的角度来认识热现象,理解“动态平衡”,这一点对学生来说有难度,同时也十分重要,在以后的学习中还会遇到。为了更直观地描述热平衡的“动态平衡”,教科书给出了“两个系统的热平衡过程”的图示。另外,为了让学生对温度的尺度有所感悟,教科书以轴向列表的方式给出了部分人们已观测的温度值。
2.应用分子动理论和统计观点解释物理概念和规律
学生在第一章中学习了分子动理论的基本知识,但并没有应用分子动理论和统计观点来系统地、深入地分析具体的物理问题,本章关于温度、气体压强等概念及气体实验定律的学习,是对分子动理论和统计观点的一次具体的应用。教科书对三个气体实验定律的设计思路是:第一,玻意耳定律的介绍方式是先让学生经历探究性实验过程,后得出结论,而盖—吕萨克定律和查理定律则是直接讲授实验结果;第二,先讨论有一个状态参量不变的特殊情况,后推导三个状态参量都改变的普遍情况;第三,先弄清宏观事实,后进行微观解释;第四,先用公式概括相关物理规律,再用 p–V 图像、V–T 图像和 p–T 图像描述这些规律。希望这样的处理,能符合大多数学生的认知规律。
另外,学生在第一章第 3 节“分子运动速率分布规律”和第 4 节“分子动能和分子势能”中已了解了气体压强和温度的微观含义,并认识到大量分子的行为将遵从一定的统计规律,以此为基础,学生将进一步理解气体实验定律的微观解释。
应该看到,学习气体的性质,对气体宏观性质和微观结构特点的认识,将为固体、液体的宏观性质及其微观解释带来很好的借鉴。教科书通过实验让学生了解气体实验定律,并用分子动理论和统计观点对气体实验定律进行具体和比较详细的解释,这样的做法具有十分重要的意义。
3.突出理想模型,渗透创新意识
理想模型是物理学中的重要思想方法,在前面学习质点、点电荷、单摆和弹簧振子等物理模型后,本章又引入了“理想气体”模型。在获得三个气体实验定律后,学生自然要询问它们的适用条件与范围。因此,教科书也是希望学生在经历气体实验定律获得的科学过程后,提出问题并深入思考,进而提炼得出“理想气体”模型。到此为止,学生在高中阶段基本完成了对主要理想模型的学习。因此,教科书专门在“理想气体”所在小节的最后设置了“科学方法”栏目,对理想模型进行归纳和概括,帮助学生认识这一重要科学方法的本质和特征,同时也对学过的重要理想模型进行梳理,从而由点成线,完善学生的知识结构。除了对象模型外,理想模型还有过程模型和条件模型。例如,匀速运动、匀变速运动、简谐运动、匀速圆周运动等都是理想的过程模型;而光滑(无摩擦)、平面、轻绳(无质量)等都是条件模型。
创新思维也是科学思维的重要组成部分。相对于理想模型的显性化介绍,创新思维在教科书中主要以渗透的方式为主,通过真实的科学故事触碰学生的思维,激发学生内在的创新动机和创新意识。在固体内容之后,教科书中的“科学漫步”栏目以“石墨烯实验研究背后的故事”为题,介绍了 2010 年诺贝尔物理学奖得主研究石墨烯背后的故事。文中先讲述了这位科学家夺得“搞笑诺贝尔物理学奖”的过程,这个研究看似搞笑,但背后却体现了细心的观察和严密的逻辑,是一个很好的提出猜想与假设的实例,也充分体现了热爱与兴趣对于研究的重要性。在制造石墨烯的研究中,这位科学家实际上也是秉承上述一贯的特点,从而取得了重大突破。最后,教科书指出创新思维在科学研究中的重要作用,即“解决具有挑战性的科学问题,除了扎实的理论和精密的仪器外,好奇心、想象力、对日常生活的细致观察和灵活运用也同样重要”。
4.宏观与微观相结合,发展学生的物质观念
人类对物质的认识是从宏观到微观不断深入的过程。在初中阶段,通过对声、光、热、电、磁、力与物质的相互作用的学习,初步认识了物质的形态和变化、物质的属性、物质的结构与物体的尺度等,这些知识为进一步认识物质的宏观特征和微观结构奠定了基础。本章内容以分子动理论为基础,在认识物质宏观特征和规律的同时,注意寻求其背后的微观机制,使学生能够从不同层次对物质的形式、变化等形成认识。例如,在介绍固体时,教科书围绕“观察食盐和松香外形有什么差别”和“观察玻璃与云母片上石蜡熔化区域的形状”两个活动来研究晶体和非晶体的宏观特征。在观察现象的基础上,从晶体的微观结构——空间点阵等方面对原因进行定性解释。对于微观解释,教科书仅要求学生了解组成晶体的微粒在空间依照一定的规则排列,对于用点阵概念来解释晶体的规则外形和各向异性,大致了解即可,不作过多要求。关于晶体的各向异性,虽然教科书既通过实验展示了云母片导热性上的各向异性,也通过图片展示了方解石光学性质的各向异性,但应当提醒学生注意,并非每种晶体都能在各种物理性质上表现出各向异性。
5.重视知识与生活的联系
本章始终重视引导学生利用所学知识解释身边现象,这点在“液体”一节中尤为突出。教科书在介绍表面张力、浸润和不浸润、毛细现象时,只要求学生对相应的现象有所认识,对背后的微观机制定性了解即可,同时,能够利用所学知识对日常现象进行解释。例如,教科书在讲解表面张力时,从实验入手,引导学生观察现象、深入思考。为了说明液体表面的收缩趋势,教科书提出了表面层的概念,要求学生初步了解表面层的形成原因,让学生知道表面层里的分子比液体内部稀疏即可。实验中,教科书强调用热针能刺破肥皂膜,这是因为液体的表面张力与温度有关,温度升高时,表面张力会减小,但同样不需要学生掌握。在介绍浸润、毛细现象时,教科书也是采用观察实验的方式来引导学生认识相关现象,最后,介绍生产生活中常见的毛细现象,将知识与生活联系起来。
液晶是现代社会中广泛采用的一种材料,与学生的生活密切相关。教科书在研究固体、液体的基础上,简单地对液晶的结构和物理特性进行了介绍。在这一基础上,教科书中的“科学漫步”栏目以“液晶显示”为题,对液晶最基本的显示原理进行了介绍,使学生能对日常生活中的液晶显示设备有所认识,为有兴趣的学生打开一扇窗户,鼓励他们了解其他显示技术。
课时安排建议
第 1 节 温度和温标 1 课时
第 2 节 气体的等温变化 2 课时
第 3 节 气体的等压变化和等容变化 1 课时
第 4 节 固体 1 课时
第 5 节 液体 2 课时
第 1 节 温度和温标 教学建议
1.教学目标
(1)知道状态参量与平衡态。
(2)知道热平衡,理解热平衡定律及温度的意义。
(3)知道温标、摄氏温标和热力学温标,知道摄氏温度与热力学温度的转换关系。
2.教材分析与教学建议
本节内容由状态参量与平衡态、热平衡与温度、温度计与温标三部分组成。教科书重点介绍了与热现象相关的一些物理概念,包括系统、状态参量、平衡态、热平衡等,并根据热平衡来定义温度。这样定义温度,使学生对温度这个物理量的理解比初中更深刻了。应提醒学生,在高中阶段对许多与温度有关的物理现象,需要用新的概念来重新认识。教科书还介绍了温标和确定温标的方法,摄氏温度与热力学温度,以及它们之间的换算关系。
本节内容比较抽象,可以通过对相似概念的比较、列举生活中的具体事例等方法帮助学生理解概念。另外,为保持学习思路的连贯,可以简要复习前一章内容,明确第一章“分子动理论”是从微观的角度研究物质、运动和相互作用的,而本章主要从宏观的角度学习气体、固体和液体的性质,并要求能用分子动理论来解释这些宏观现象。
(1)问题引入
本节“问题”栏目中的情境是为引出热学研究中的基本概念而设计的。把不同压强、不同温度的气体混合在同一容器中,如果容器与外界没有能量交换,经过一段时间后,容器内的气体会是什么状态?很明显,教科书中问题的设计直接要求学生关注容器中的气体压强、温度等物理量及其变化情况。让学生初步感受到在热学问题研究中,需要首先明确研究对象,以及用于描述和确定研究对象状态的物理量,为“系统”“状态参量”“平衡态”等概念的引入作好铺垫。
(2)状态参量与平衡态
教科书指出,气体作为热力学系统是由大量分子组成的,而外界可以与系统有相互作用。在以往的学习中,学生已经学习过动力学中的多物体系统、机械能守恒中的系统、动量守恒中的系统,等等,也理解除重力以外的其他力做功、外力的冲量等“外界”对系统总机械能、总动量的影响。应突出热力学系统最大的特征——系统内分子数的“大量”,为后续用统计观点解释气体实验定律埋下伏笔。
①状态参量
教学中要引导学生认识到,在以前的学习中,为了描述质点所处的状态,我们引入了速度、动量、能量等状态量。在热学中,为了确定系统的空间范围、外界与系统之间或系统内部各部分之间力的作用以及系统的冷热程度,需要引入体积、压强和温度三个状态参量。它们是描述热力学系统状态的基本物理量。
②平衡态
平衡态和非平衡态的概念十分抽象,教学中可继续以“问题”栏目中的情境为例。如果容器与外界没有能量交换,当打开挡板后,气体状态会发生变化,变化过程是非平衡态。最终稳定下来的状态是容器内压强、温度变得相同,系统达到平衡态。当系统处于平衡态时,系统所有状态参量都不随时间变化,即体积、压强和温度都不随时间变化。引导学生关注平衡态和非平衡态在状态上的差异,引出平衡态概念。
怎样帮助学生理解平衡态概念中“在没有外界影响的情况下”的条件呢?
在外界影响下,系统也可以处于一种宏观性质不随时间变化的状态,但这不是平衡态。例如,一根长铁丝,一端插入 100℃ 的沸水中,另一端放在 0℃ 恒温源中,经过足够长时间,温度沿铁丝有一定的分布,而且不随时间变化,这种状态不是平衡态,只是一种稳定状态,因为存在外界的影响,当撤去外界影响,系统各部分的状态参量就会发生变化。
(3)热平衡与温度
教科书指出,平衡态是指在没有外界影响的情况下,只要经过足够长的时间,系统内各部分的状态参量能够达到的稳定状态;而热平衡是指如果两个系统相互接触而传热,这两个系统的状态参量将会互相影响而分别改变,经过一段时间,各自的状态参量就不再变化了,这说明两个系统达到了平衡。可见,平衡态是针对某个系统而言的,而热平衡是针对两个相互作用的系统而言的。
在初中物理中,将温度定义为“表示物体冷热程度的物理量”,这是对温度的一个通俗解释。温度的严格定义及测量原理是建立在热平衡定律基础上的。两个系统处于热平衡时,它们具有一个“共同的热学性质”,表征这一“共同的热学性质”的物理量就被定义为温度。教学中,可在初中“温度”定义的基础上,通过实验展示传热过程中两系统“温度”的变化,引导学生体会“共同的热学性质”指的是什么,帮助学生在热平衡定律的基础上深化“温度”的定义。教科书还通过轴向列表给出了“人们已观测的温度”,目的是让学生了解自然界中温度的尺度。
教学片段
热平衡
实验器材 DIS 实验系统(温度传感器两个),泡沫容器(带盖),铝块(顶端开有小孔,用于插入温度传感器),热水和冷水。
实验操作 把浸在热水中的铝块取出,再放入泡沫容器的冷水中,盖上盖子。用两个温度传感器分别测量铝块和水的温度,由 DIS 实验系统实时绘制两个温度随时间变化的曲线。
实验观察 绘制的曲线如图 2– 1所示,铝块的温度降低,水的温度升高,两者相等后保持不变。
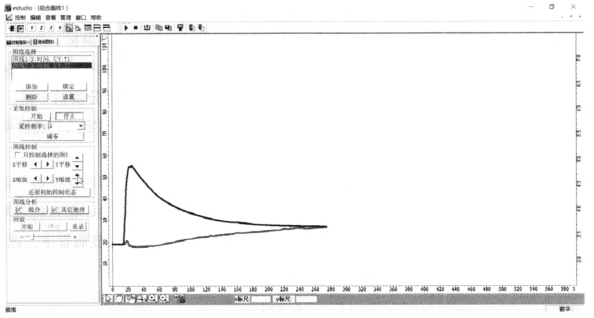
科学推理 热铝块和冷水相互接触而传热,由于两个系统冷热程度不同,铝块放出热量,水吸收热量。两者的冷热程度差异随着时间的推移而慢慢变小,最终,它们的冷热程度相同,两者之间不再传递热量,这种状态将保持稳定。
实验结论 当铝块和水不再传递热量时,铝块和水处于热平衡状态。两个达到热平衡的系统具有相同的温度。
实验注意事项 该热平衡实验装置示意图如图 2–2 所示。泡沫容器可采用红酒瓶泡沫包装。
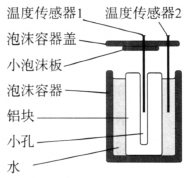
- 铝块所开小孔直径略大于温度传感器直径,深度略短于传感器长度。温度传感器插入小孔后底端要能接触铝块。
- 盖上盖子后,一般铝块顶部与盖子之间会有空隙,可垫一小泡沫板。小泡沫板的厚度要合适,既不能影响盖子的密封性,又要能避免容器内空气对温度传感器 1 的影响。
- 由于铝块的导热性能好,温度变化又是先快后慢,在盖盖子和插传感器的一小段时间内,铝块的温度变化幅度很大,会使铝块和水的有效测量温差比初始温差小。实验时可以先把温度传感器插在泡沫盖上,缩短铝块和水接触后到正式记录数据的时间间隔。另外,应设法增大水和铝块的初始温差,例如也可以用冰过的铝块与开水进行传热。
初中学习的许多热现象,现在都可以用新的概念来重新认识。例如,对于本节“练习与应用”中的第 1 题,如果用“热平衡”等概念来认识“测定金属块的比热容”的实验过程,那么对实验过程的认识就上升了一个层次。
(4)温度计与温标
热平衡定律给出了温度的宏观定义,也为温度的测量提供了理论依据。因为互为热平衡的物体具有相同的温度,所以比较各物体时,不需要将各个物体直接接触,只需将作为标准物体的温度计分别与各个物体接触,即可比较各物体温度的高低。实验室里常用温度计(接触式)的原理是:一切互为热平衡的系统都具有相同的温度。温度计就是我们选择的标准物体,温度计与待测物体接触,使它们达到热平衡,标准物体所表示的就是待测物体的温度。温度计的热容量必须很小,以便它与待测物体接触并进行热交换时,几乎不改变待测物体的状态。
为了表示出物体温度的数值,对温度零点、分度方法所做的规定,就是温标。生活中常见的有摄氏温标、华氏温标等。不同的温标都包含三个要素:第一,选择某种具有测温属性的测温物质;第二,了解测温物质随温度变化的函数关系;第三,确定温度零点和分度的方法。1848 年开尔文建立了热力学温标,它不依赖于测温物质的具体性质。由热力学温标定义的温度叫热力学温度,热力学温度的单位开尔文是国际单位制中七个基本单位之一。
教科书图 2.1–2 介绍了伽利略的温度计的构造,可以让感兴趣的同学自己动手做一做。教学中,可以用图中所示的玻璃壶,也可以用烧杯代替。烧瓶上用单孔橡皮塞插一根长玻璃管,先用双手捂住烧瓶,使其中的空气膨胀,然后倒插入烧杯的水中,水会被吸入玻璃管中。固定烧瓶,根据玻璃管中水面的移动,可以检测温度的变化。
3.“练习与应用”参考答案与提示
本节共 4 道习题。第 1 题考查学生对热平衡知识点的掌握情况,属于理解层次。第 2 题考查对两种温标的简单换算。第 3 题是对两种温标换算关系的拓展训练。第 4 题涉及闭合电路的欧姆定律,对学生的能力要求较高。
1.在以上叙述中,有两个地方涉及“热平衡”。第一处是金属块放在沸水中,经过一段时间后,金属块和沸水组成的系统温度相同,这两个系统达到“热平衡”。第二处是将金属块迅速放入质量已知、温度已知的水中,并用温度计测水温,当水温不再升高,这时金属块、水和温度计组成的系统温度相同,它们也达到了“热平衡”。
2.300.15 K;− 270.65℃
提示:由 T = t + 273.15 K,得 T =(27 + 273.15)K = 300.15 K;t =(2.5 – 273.15)℃ = − 270.65℃。
3.X = kT;X = k(273.15 + t);X–T 图像和 X– t图像如图 2–3 和图 2–4 所示。
提示:设比例系数为 k,则 X = kT。由 T = t + 273.15 K,可得 X = k(273.15 + t)。在直角坐标系中画出 X–T 图像和 X–t 图像,如图 2–3 和图 2–4 所示。
4.t1 点标在电流较大的刻度上。
提示:由 R–t 图像可知,电阻 R 随温度 t 的升高而变大。因为 t1 点时电阻较小,由于电路的电动势和内阻不变,根据闭合电路的欧姆定律,电流较大。
发布时间:2021/1/8 下午9:46:56 阅读次数:4811
