表  氧气分子的速率分布

速率区间 /（m·s−1）		100 以下	100 ~ 200	200 ~ 300	300 ~ 400	400 ~ 500	500 ~ 600	600 ~ 700	700 ~ 800	800 ~ 900	900 以上
各速率区间的 分子数 占总分子数的 百分比	0 ℃	1.4	8.1	17.0	21.4	20.4	15.1	9.2	4.5	2.0	0.9
	100 ℃	0.7	5.4	11.9	17.4	18.6	16.7	12.9	7.9	4.6	3.9

 

 

第 3 节  分子运动速率分布规律  教学建议

1．教学目标

（1）初步了解什么是统计规律。

（2）了解气体分子运动的特点：分子沿各个方向运动的机会均等，分子速率按一定规律分布。

（3）能用气体分子动理论解释气体压强的微观意义，知道气体的压强与所对应的微观物理量间的联系。

2．教材分析与教学建议

分子运动速率分布规律是对第 1 节“分子动理论的基本内容”的拓展和延伸。分子在做永不停息的无规则运动，通过对气体分子运动速率分布规律的研究，可进一步研究气体的热现象。本节内容由气体分子运动的特点、分子运动速率分布图像和气体压强的微观解释三部分组成。

在气体分子运动的特点中，教科书指出，气体分子的分布虽然稀疏，但单位体积内的分子数目仍大得惊人，气体分子速率分布规律是大量分子集体行为的反映，具有统计的意义。本节教科书有意识地向学生渗透统计观点，首先，通过伽尔顿板实验提出统计规律，教学中也可以通过生活中的一些事例，比如掷硬币，说明统计规律的普遍性。教科书利用统计规律说明气体分子运动的特点，即气体分子沿各个方向运动的机会均等。关于分子运动速率的分布，教科书根据氧气分子运动速率的实验数据，进行分析讨论，得到分子速率总是表现出“中间多，两头少”分布的统计规律，在温度升高时，气体分子的速率增大，并通过图像让学生直观地体会“温度越高，分子的热运动越剧烈”的含义。最后，教科书从分子动理论的观点出发，论述了气体对容器的压强源于气体分子的热运动，是大量气体分子作用在器壁单位面积上的平均作用力，从而揭示了宏观性质的微观本质。

（1）问题引入

伽尔顿板是统计规律演示装置，它的腔内分为储存室、钉阵和狭槽三部分。粒子储存室位于腔的上部，称为漏斗；钉阵位于腔的中部，由铁钉组成；钉阵下方有狭槽。

实验原理：小球从漏斗口落下，在到达底部前，与钉子发生碰撞。对于单个的小球，落到底部的哪一条狭槽完全是随机的、不确定的。但如果不断地从漏斗口放入小球，当小球数量较多时，在伽尔顿板的底部各狭槽内就都会有一定数量的小球，且中间狭槽的小球最多，两边狭槽的小球较少。也就是说，对于大量的小球，落到各狭槽的分布满足一定的统计规律。

进行实验并观察实验现象。

①拔出插片，将伽尔顿板倒置，待小球全部进入储存室后，再将插片插入漏斗口处，将伽尔顿板正立过来，置于水平桌面上。

②拔出插片，大量小球下落，观察小球在底部各狭槽的分布状态。

③重复实验多次，可以观察到大量偶然事件所服从的统计规律。

教学时，还应要求学生从联系实际角度列举具有“统计规律”的生活实验与社会现象，进一步加深对“统计规律”的了解，从中领略自然与社会的奇妙与和谐，增加对科学的好奇心与求知欲，体验探索自然规律的艰辛与喜悦。

（2）气体分子运动的特点

教科书指出，要研究气体的热现象，就要先了解气体分子运动的特点。由于气体分子之间的距离大约是分子直径的 10 倍，分子的大小相对分子间的空隙来说很小，可以把气体分子视为质点，同时，气体分子间的作用力很小，可忽略。因此，除了相互碰撞或者跟器壁碰撞外，气体分子不受力的作用，在空间自由移动，气体能充满它所能达到的空间，没有一定的体积和形状。每个气体分子都在做永不停息的运动，由于分子间距很小，分子数量巨大，分子运动的速率较大，因此，大量气体分子频繁地发生碰撞，使每个气体分子都在做杂乱无章的运动。每个分子的运动方向时刻在变化，对大量分子来说它们向各个方向运动的概率是相等的。大量气体分子的热运动，在宏观上表现出一定的规律性，即气体分子沿各个方向运动的数目是相等的。

（3）分子运动速率分布图像

尽管分子做无规则运动，速率有大有小，但大量分子的速率遵循统计规律。在任一时刻，速率很大和速率很小的分子的个数所占的比例相对较少，大多数分子的速率和平均速率相差很小。教科书给出了氧气分子在 0℃ 和 100℃ 时的速率分布的表格和图像，在此基础上，可让学生定性解释“温度越高，分子的热运动越剧烈”的含义。

（4）气体压强的微观解释

气体的压强是大量分子与器壁频繁碰撞的结果。单个分子碰撞器壁的作用力是短暂的，但是大量分子频繁地碰撞器壁，就对器壁产生持续、均匀的压力。所以，从分子动理论的观点来看，气体的压强就是大量气体分子作用在器壁单位面积上的平均作用力。教科书选择了一个与器壁发生正碰的分子为研究对象，通过理论推导得出器壁所受的作用力，让学生体会到分子对器壁的碰撞确实产生了作用力，大量分子对器壁的撞击产生了压强，揭示了宏观性质的微观本质。在此基础上，教科书还设计了用豆粒做气体分子模型来模拟气体压强产生机理的演示实验，引导学生利用统计的思想去思考问题，加深对气体压强的微观解释的认识。

 

教学片段

气体压强的微观解释

提出问题        封闭在容器中的气体，为什么会对容器壁产生压力，从而形成压强呢？

分析讨论        图 1–5 是容器中气体分子运动的示意图。相对于气体分子直径的大小，气体分子之间的距离很大，可认为分子间的作用力为 0。但是，气体分子数量巨大，且具有较大的运动速率，因此，它们会相互碰撞，也会与容器壁发生碰撞。选择一个与器壁发生正碰的质量为m、速度大小为 v 的气体分子为研究对象，如图 1–6 所示。由于是弹性碰撞，根据动量定理和牛顿第三定律，让学生求出器壁受到的作用力。同理，可求出气体分子与器壁斜碰时的作用力。大量气体分子不断地撞击器壁，从而产生气体对容器的压强。

提出问题        这种撞击是不连续的，为什么器壁受到的作用力却是均匀不变的呢？

模拟实验 1    向秤盘上倒豆粒的实验，形象地模拟了气体压强产生的机理。单颗豆粒给秤盘的压力很小，作用时间也很短；大量豆粒对秤盘的频繁碰撞，对秤盘产生了持续、均匀的压力；豆粒与秤盘碰撞时的速率越大，对秤盘产生的压力也越大。

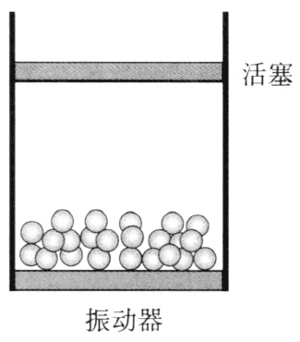
模拟实验 2    塑料小球在容器内碰撞的实验，同样可以模拟气体压强产生的机理。在玻璃筒内装入一些塑料小球，这些小球代表气体分子。在小球上面放一轻质活塞，用电动机带动一振动器使小球运动（图 1–7）。当电动机启动后，活塞受小球的撞击，悬浮在一定的高度。增大电动机的转速或增加小球的数目，活塞悬浮的高度都会增加。实验现象说明分子的动能越大，压强越大。当动能不变时，分子的数密度越大，压强越大。

归纳总结        大量分子不停地碰撞会对容器壁产生持续、均匀的压力，从而形成压强。气体分子的平均速率越大、分子的数密度越大，气体的压强就越大。

---

对气体压强的微观解释要注意：气体压强是由大量分子与器壁的频繁碰撞所产生的，它的大小与分子的平均动量的大小有关，与单位时间在单位面积上碰撞的分子个数有关。当分子数密度不变时，温度升高，不仅碰撞的平均动量增加了，而且由于速率的增加，器壁在单位时间、单位面积上受到分子碰撞的次数也增加了。

3．“练习与应用”参考答案与提示

本节共 4 道习题。第1题和第3题要求从气体的质量、温度和体积等角度辨析不同因素对压强的影响。第 2 题考查分子运动速率分布的特点。第4题从共享单车、大数据出发，让学生规划公交线路，很具有时代性，启发学生对生活中的事物要多观察、多思考，应用已学知识解决实际问题，培养学生的社会责任感。

 

1．有区别。从微观上看，一定质量的气体体积不变仅温度升高，气体分子的平均速率增大，单位时间内、单位面积上气体分子与器壁的碰撞对器壁的作用力增大，压强增大。一定质量的气体温度不变仅体积减小，气体分子的数密度增大，则在单位时间内与单位面积器壁碰撞的分子数增多，压强增大。

 

2．相同点：都呈现“中间多、两头少”的分布。

不同点：这两个温度下具有最大比例的速率区间是不同的。0℃ 时速率在 300 ~ 400 m/s 的分子最多；100℃ 时速率在 400 ~ 500 m/s 的分子最多。100℃ 的氧气，速率大的分子比例较多，其分子的平均速率比 0℃ 的大。

 

3．（1）乙的压强小于 p。甲、乙的质量、温度相同，但乙的体积大于甲的体积，则乙的气体分子的数密度小，在单位时间内与单位面积器壁碰撞的分子数就少，故压强就小。

（2）丙的压强大于 p。甲、丙的质量、体积相同，但丙的温度高于甲的温度，则丙的气体分子的平均速率大，单位时间内、单位面积上气体分子与器壁的碰撞对器壁的作用力就大，故压强就大。

（3）丁的压强大于 p。甲、丁的体积相同，但丁的质量大于甲的质量，丁的温度高于甲的温度，则丁的气体分子的数密度大，分子的平均速率大，在单位时间内与单位面积器壁碰撞的分子数多，对器壁的作用力也大，故压强大。

 

4．统计各区域、各时段沿不同道路骑行的人数，可以用来设计公交车线路的数量和走向。在确定公交线路走向之后，统计相同时段、沿相关方向骑行不同路程的人数，可以作为设置公交车车站位置的参考。除此之外，还可以统计早、中、晚不同时段在相同时间内沿指定方向骑行的人数，作为制订公交车在不同时段发车时刻表的参考。