第七章 复习与提高

A组

1．一位同学根据向心力公式 F＝m\(\frac{{{v^2}}}{r}\) 说，如果人造地球卫星的质量不变，当轨道半径增大到2倍时，人造地球卫星需要的向心力减小为原来的 \(\frac{1}{2}\)；另一位同学根据卫星的向心力是地球对它的引力，由公式 F＝G\(\frac{{{m_1}{m_2}}}{{{r^2}}}\) 推断，当轨道半径增大到 2 倍时，人造地球卫星需要的向心力减小为原来的 \(\frac{1}{4}\)。哪位同学的看法对？说错了的同学错在哪里？请说明理由。

2．发射人造地球卫星时将卫星以一定的速度送入预定轨道。发射场一般选择在尽可能靠近赤道的地方。这样选址有什么优点？

3．你所受太阳的引力是多大？和你所受地球的引力比较一下，可得出怎样的结论？已知太阳的质量是 1.99×10³⁰ kg，地球到太阳的距离为 1.5×10¹¹ m，设你的质量是 60 kg。

4．地球质量大约是月球质量的 81 倍，一个飞行器在地球与月球之间。当地球对它的引力和月球对它的引力大小相等时，该飞行器距地心的距离与距月心的距离之比为多少？

5．海王星的质量是地球的 17 倍，它的半径是地球的4倍。绕海王星表面做圆周运动的宇宙飞船，其运行速度有多大？

6．在月球上的宇航员，如果他已知引力常量和月球半径，且手头有一个已知质量为m的砝码。

（1）他怎样才能测出月球的质量，写出月球质量的表达式。

（2）他需要选用哪些实验器材。

7．某中子星的质量大约与太阳的质量相等，为 2×10³⁰ kg，但是它的半径只有 10 km。

（1）求此中子星表面的自由落体加速度。

（2）贴近中子星表面，求沿圆轨道运动的小卫星的速度。

B组

1．如果你站在月球上，能否用一把刻度尺和一块秒表估测月球的质量？如果能，请设计实验，并说出需要测量的数据和月球质量的计算式。已知月球的半径为 R。

2．行星的平均密度是 ρ，靠近行星表面运行的卫星运转周期是 T，证明：ρΤ² 是一个常量，即对任何行星都相同。

3．有一质量为 m、半径为 R、密度均匀的球体，在距离球心 O 为 2R 的地方有一质量为 mʹ 的质点。现从m中挖去半径为 \(\frac{1}{2}\)R 的球体，如图 7-1 所示，则剩余部分对 mʹ 的万有引力F为多少？

4．利用三颗位置适当的地球同步卫星，可使地球赤道上任意两点之间保持无线电通信，目前地球同步卫星的轨道半径为地球半径的6.6倍。假设地球的自转周期变小，若仍仅用三颗同步卫星来实现上述目的，则地球自转周期的最小值约为多少小时？

5．海边会发生潮汐现象，潮来时，水面升高；潮退时，水面降低。有人认为这是由于太阳对海水的引力变化以及月球对海水的引力变化所造成的。中午，太阳对海水的引力方向指向海平面上方；半夜，太阳对海水的引力方向指向海平面下方；拂晓和黄昏，太阳对海水的引力方向跟海平面平行。月球对海水的引力方向的变化也有类似情况。太阳、月球对某一区域海水引力的周期性变化，就引起了潮汐现象。

已知太阳质量为 2.0×10³⁰ kg，太阳与地球的距离为 1.5×10⁸ km，月球质量为 7.3×10²² kg，月球与地球的距离为 3.8×10⁵ km，地球质量为 6.0×10²⁴ kg，地球半径取 6.4×10³ km。请你估算一下：对同一片海水来说，太阳对海水的引力、月球对海水的引力，分别是海水重力的几分之一？

6．太阳系各行星几乎在同一平面内沿同一方向绕太阳做圆周运动。当地球恰好运行到某地外行星和太阳之间，且三者几乎排成一条直线的现象，天文学称为“行星冲日”。已知地球及各地外行星绕太阳运动的轨道半径如下表所示。

根据题中信息，试计算木星相邻两次冲日的时间间隔，哪颗地外行星相邻两次冲日的时间间隔最短？

复习与提高参考答案与提示

A 组配置了 7 道习题。第1题辨析卫星的向心力公式，练习理想模型的构建。第 2 题通过对卫星发射场选址的分析，一方面明确了人造地球卫星的运行速度是相对于地心而不是地表，另一方面也为下一章从节能的角度渗透科学态度和责任方面的要求。第3题比较太阳和地球对人的万有引力大小，通过计算结果分析太阳引力和地球引力对人的影响。第4题地球和月球之间有一个平衡点，通过求平衡点的位置，可以适当拓展介绍拉格朗日点。第5题求海王星的第一宇宙速度。第 6 题要求学生完成在月球上测月球质量的实验设计，具有一定的开放性。第7题求中子星表面的自由落体加速度和中子星的第一宇宙速度，研究对象有卫星、行星、恒星、中子星（恒星的不同演化阶段），从这些数据中认识到恒星质量和密度大到一定程度时发生的现象，进而预测和解释黑洞等问题。

B组配置了 6 道习题。第 1 题要求学生完成在月球上测月球质量的另一种方法。第 2 题要求学生证明 ρT² 是一个常量。第 3 题用割补法计算万有引力，是典型模型的转化。第 4 题求三颗同步卫星对应地球的最小自转周期，将卫星的周期与地球的自转联系起来，找到“最小”这个临界条件，并将它转化力卫星轨道的表达。第 5 题是潮汐现象的一种解释，理论联系实际。第 6 题涉及行星冲日现象，从定性到定量逐渐认识行星运行速率与轨道半径的关系，解释和预测行星冲日现象，达到学以致用的目的。

A组

1．第二个同学说的对，第一个同学说错了。

根据万有引力提供向心力可知 G\(\frac{{{m_地}m}}{{{r^2}}}\) ＝ m\(\frac{{{v^2}}}{r}\)，v ＝ \(\sqrt {\frac{{G{m_地}}}{r}} \)，即当半径增大到 2 倍时，v 变为原来的 \(\frac{1}{{\sqrt 2 }}\)。

2．在发射卫星时，相对于地心的速度越大，越容易发射出去，相对于地心的发射速度等于相对于地面的发射速度加上地球自转的线速度。地球上不同地方角速度大小相等，赤道处半径最大，由 v＝ωR 可得出赤道处自转的线速度最大。故发射场一般选择在尽可能靠近赤道的地方。

提示：进一步明确卫星的速度是相对于地心的速度，而不是相对于地表的速度，为了节省能量，可以利用地球的自转，合理选址。引导学生读新闻报道时关注卫星发射地所在的纬度。

3．地球半径 6.4×10⁶ m 与地球到太阳的距离 1.5×10¹¹ m 相比，相差近 10 万倍，因此人距太阳的距离可以认为也是 1.5×10¹¹ m，故人受太阳的引力 F ＝ G\(\frac{{{m_太}m}}{{{r^2}}}\) ＝ 6.67×10^-11×\(\frac{{1.99 \times {{10}^{30}} \times 60}}{{{{(1.5 \times {{10}^{11}})}^2}}}\) N ＝ 0.35 N。

人受地球的引力 Fʹ＝ mg ＝ 60×9.8 N ＝ 588 N。

可以看到，人受太阳的引力远小于人受地球的引力。因为引力不仅仅与物体质量有关，还与物体之间的距离有关，所以尽管太阳质量很大，但是距离很远，所以对处于地球上的人的引力很小。

4．9∶1

提示：设月球的质量为 m₀，则地球的质量是 81m₀，假设飞行器距离地心距离为 R，距离月心距离为 r，飞行器的质量是 m，月球的质量是 m₀，那么飞行器和地球间的引力为 F₁ ＝ G\(\frac{{81{m_0}m}}{{{R^2}}}\)，飞行器和月球间的引力为 F₂ ＝ G\(\frac{{{m_0}m}}{{{r^2}}}\)，由于F₁ ＝ F₂，故 R∶r ＝ 9∶1。

5．16.3 km/s

提示：宇宙飞船的运行半径等于海王星的半径 R，其线速度v为近地卫星的线速度，根据万有引力提供向心力可知 G\(\frac{{{m_海}m}}{{{R^2}}}\)＝m\(\frac{{{v^2}}}{R}\)，得出 v ＝ \(\sqrt {\frac{{G{m_海}}}{R}} \)。同理地球的第一宇宙速度 v₁ ＝ \(\sqrt {\frac{{G{m_地}}}{R_地}} \)，由此联立解得 \(\frac{v}{{{v_1}}}\)＝\(\sqrt {\frac{{{m_海}{R_地}}}{{{m_地}{R_海}}}} \) ＝ \(\frac{{\sqrt {17} }}{2}\)。即 v＝ \(\frac{{\sqrt {17} }}{2}\) v₁ ＝ \(\frac{{\sqrt {17} }}{2}\)×7.9 km/s ≈ 16.3 km/s。

6．方案一：用测力计测出钩码重力 W_钩，则月球表面重力加速度 gʹ ＝ \(\frac{{{W_钩}}}{m}\)，由万有引力定律可得 gʹ ＝ \(\frac{{G{m_月}}}{{{R^2}}}\)，联立解得月球的质量 m_月 ＝ \(\frac{{{W_钩}{R^2}}}{{Gm}}\)。

在此方案中，需要使用的测量工具是测力计。

方案二：将钩码从空中适当高处由静止释放，测出其下落高度 h 和下落时间 t，则 h ＝ \(\frac{1}{2}\)gʹt²，由万有引力定律可得 gʹ ＝ \(\frac{{G{m_月}}}{{{R^2}}}\)，联立解得月球质量 m_月 ＝ \(\frac{{2{R^2}h}}{{G{t^2}}}\)。

在此方案中，需要使用的测量工具是刻度尺和停表。

提示：测天体的质量，所求天体一定要位于中心天体的位置。已知万有引力常量 G，环绕天体的轨道半径、线速度、角速度、周期四个量中知道任意两个就可以求出中心天体的质量。本题已知天体半径 R，两种方案都是围绕测出天体表面的重力加速度来进行设计，即相当于已知轨道半径和加速度，求中心天体的质量。

7．（1）1.3×10¹² m/s²；（2）1.1×10⁸ m/s

提示：（1）设中子星表面的自由落体加速度为 g，由 G\(\frac{{{m_中}m}}{{{R^2}}}\) ＝ mg 解得 g ＝ \(\frac{{G{m_中}}}{{{R^2}}}\) ＝ 1.3×10¹² m/s²。

（2）贴近中子星表面，沿圆轨道运动的小卫星的速度为 v，由万有引力提供向心力可知 G\(\frac{{{m_中}m}}{{{R^2}}}\) ＝ m\(\frac{{{v^2}}}{r}\)，又因 G\(\frac{{{m_中}m}}{{{R^2}}}\) ＝ mg，联立解得 v ＝ \(\sqrt {gR} \) ＝ \(\sqrt {1.3 \times {{10}^{12}} \times {{10}^4}} \) m/s ＝ 1.1×10⁸ m/s。

计算了金星、地球、海王星等行星表面的重力加速度和第一宇宙速度，再计算中子星表面的重力加速度和第一宇宙速度，引导学生认识到由于天体密度的不同会导致一些神奇的现象，如黑洞、光线弯曲，等等。

B组

1．用刻度尺测出某点距月球表面的高度为 h，用停表测出小球从这点下落高度 h 时所用的时间 t，则 h＝\(\frac{1}{2}\)gʹt²，由万有引力定律可得 gʹ ＝ \(\frac{{G{m_月}}}{{{R^2}}}\)。联立得出月球质量 m_月 ＝ \(\frac{{2{R^2}h}}{{G{t^2}}}\)。

2．将行星看作球体，设半径为 R，质量为 m_星，则行星的密度为 ρ ＝ \(\frac{m_星}{V}\) ＝ \(\frac{{{m_星}}}{{\frac{{4\pi {R^3}}}{3}}}\)。

卫星贴近行星表面运行时，运动半径为 R，由万有引力提供向心力可知 G\(\frac{{{m_星}m}}{{{R^2}}}\) ＝ m(\(\frac{{2\pi }}{T}\))²R，即 m_星 ＝ \(\frac{{4{\pi ^2}{R^3}}}{{G{T^2}}}\)。由此可以解得 ρT² ＝ \(\frac{{3\pi }}{G}\)，式中 G 为万有引力恒量，可见 ρT² 是一个对任何行星都相同的常数。

提示：贴着行星表面飞行，只要有一个计时工具就可以知道行星的密度。

3．\(\frac{{7Gmm'}}{{36{R^2}}}\)

提示：根据万有引力定律，质量为m的球体对质点 mʹ 的万有引力 F₁ ＝ G\(\frac{{mm'}}{{{{(2R)}^2}}}\)。挖去的球体的质量 m₀ ＝ \(\frac{{\frac{4}{3}\pi {{(\frac{R}{2})}^2}}}{{\frac{4}{3}\pi {R^2}}}\)m ＝ \(\frac{m}{8}\)，那么质量为 m₀ 的球体对质点mʹ的万有引力 F₂ ＝ G\(\frac{{{m_0}m'}}{{{{(R + \frac{R}{2})}^2}}}\) ＝ G\(\frac{{{m_0}m'}}{{18{R^2}}}\)。剩余部分对质点mʹ的万有引力 F ＝ F₁ － F₂ ＝ G\(\frac{{{m_0}m'}}{{4{R^2}}}\) － G\(\frac{{{m_0}m'}}{{18{R^2}}}\) ＝ \(\frac{{7Gmm'}}{{36{R^2}}}\)。

质量分布均匀的球体之间的万有引力可以等效为质量集中在两球心的两个质点之间的万有引力，直接代公式可求。本题采用先填补成完整的球体，再减去补上的小球部分产生的引力。

4．4 h

提示：地球自转周期变小，卫星要与地球保持同步，则卫星的公转周期也应随之变小，由 G\(\frac{{{m_地}m}}{{{r^2}}}\) ＝ m\(\frac{{4{\pi ^2}}}{{{T^2}}}\)r，可得 T ＝ \(\sqrt {\frac{{4{\pi ^2}{r^3}}}{{G{m_地}}}} \)，故卫星离地球的高度变小。卫星的周期由轨道半径决定。要想仅用三颗同步卫星来实现地球赤道上任意两点之间保持无线电通信的目的，最小的轨道半径对应的几何关系为卫星连线正好和地球相切。由此关系可推出最小半径，得到最小周期。要实现三颗卫星覆盖全球的目的，当卫星的几何关系如图7-4所示时，卫星的公转周期最小，地球的自转周期也最小。

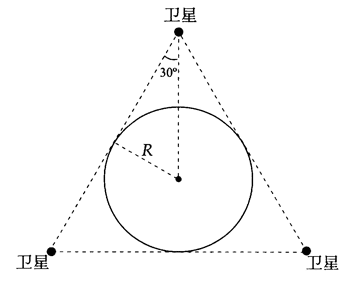
由几何关系可知，卫星的轨道半径 r ＝ \(\frac{R}{{\sin 30^\circ }}\) ＝ 2R，由开普勒第三定律可知 \(\frac{{r_1^3}}{{T_1^2}}\) ＝ \(\frac{{r_2^3}}{{T_2^2}}\)，代入题中数据得 \(\frac{{{{(6.6R)}^3}}}{{{{24}^2}}}\) ＝ \(\frac{{r^3}}{{T_2^2}}\)，由此解得 T₂ ≈ 4 h。

5．对同一片海水来说，太阳对海水的引力、月球对海水的引力，分别是海水重力的 6.1×10^-4 倍、3.4×10^-6 倍。

提示：设太阳的质量为 m_太，太阳与地球的距离为 R₁。月球质量为 m_月，月球与地球的距离为 R₂。地球的质量为 m_地，地球半径为 R，一片海水的质量为 m。

根据万有引力定律，太阳对海水的引力为 F₁ ＝ G\(\frac{{{m_太}m}}{{R_1^2}}\)，月球对海水的引力为 F₂ ＝ G\(\frac{{{m_月}m}}{{R_2^2}}\)；地球对海水的引力为 F ＝ G\(\frac{{{m_地}m}}{{R^2}}\)。因此，\(\frac{{{F_1}}}{F}\) ＝ \(\frac{{{m_太}}}{{{m_地}}}\)(\(\frac{R}{{{R_1}}}\))² ＝ \(\frac{{2.0 \times {{10}^{30}}}}{{6.0 \times {{10}^{24}}}}\)×(\(\frac{{6.4 \times {{10}^6}}}{{1.5 \times {{10}^{11}}}}\))² ＝ 6.1×10^-4， \(\frac{{{F_2}}}{F}\) ＝ \(\frac{{{m_月}}}{{{m_地}}}\)(\(\frac{R}{{{R_2}}}\))² ＝ \(\frac{{7.3 \times {{10}^{22}}}}{{6.0 \times {{10}^{24}}}}\)×(\(\frac{{6.4 \times {{10}^6}}}{{3.8 \times {{10}^{8}}}}\))² ＝ 3.4×10^-6。

本题简要介绍了对潮汐现象的一种解释，估算了太阳和月球对同一片海水的引力与重力的比较，让学生初步尝试用万有引力定律解释潮汐现象。

6．1.1 年，海王星相邻两次冲日的时间间隔最短。

提示：行星相邻两次冲日的时间间隔就是地球比该行星多运动一周的时间，设相邻两次冲日的时间间隔为 t，有 \(\frac{t}{{{T_地}}}\) － \(\frac{t}{{{T_行}}}\) ＝ 1，即 t ＝ \(\frac{1}{{\frac{t}{{{T_地}}}  -  \frac{t}{{{T_行}}}}}\) ＝ \(\frac{{{T_地}}}{{1 - \frac{{{T_地}}}{{{T_行}}}}}\)，根据开普勒第三定律有 \(\frac{{R_地^3}}{{T_地^2}}\) ＝ \(\frac{{R_行^3}}{{T_行^2}}\)，即\(\frac{{{T_地}}}{{{T_行}}}\) ＝ \({\left( {\frac{{{R_地}}}{{{R_行}}}} \right)^{\frac{3}{2}}}\) ，故 t ＝ \(\frac{{{T_地}}}{{1 - \sqrt {\frac{{R_地^3}}{{R_行^3}}} }}\)，由此可得 t ≈ 1.1 年。海王星的轨道半径最大，海王星相邻两次冲日的时间间隔最短。

行星冲日现象可类比田径场跑道上的运动员的追击相遇问题。轨道半径越大的行星周期越长，轨道半径越小的行星周期越短，周期短的不断超越周期长的。地外行星的周期都比地球的周期长，地球的周期最短，每超越一次就发生一次冲日。行星与地球的周期相差越大，冲日的周期就越短。

发布时间：2020/10/5 下午4:55:23  阅读次数：2119